Глава 18 дифференциальные уравнения высшего порядка 18.1. основные понятия

Глава 18 дифференциальные уравнения высшего порядка 18.1. основные понятия

Рассмотрим одну из задач, связанную с дифференциальным уравнением второго порядка.

V Пример 1. На тело, движущееся по прямой, в направлении движения действует некоторая постоянная сила. Найти, как зависит путь, пройденный телом, от времени.

Решение. Обозначим длину пути через s, а время — через t. Постоянная сила вызывает постоянное ускорение, которое обозначим через д. Поскольку ускорение есть вторая производная пути по времени, получаем следующее дифференциальное уравнение:

d2s

—т = а = const.

dt2 и

Это обыкновенное дифференциальное уравнение второго порядка. Поскольку

d2s d Ids

—т = ~г -г — Я — const, dt2 dt dtj у

то

ds

где C — произвольная постоянная. Следовательно, скорость тела ^ есть линейная функция времени. Если в начальный момент

времени (t = 0) скорость тела равнялась 0, то

в противном случае С — величина начальной скорости (s'(0) = = С). После вторичного интегрирования получаем

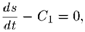8 = а(і) = Ц+ Сіі + С2,

где С2 — произвольная постоянная. Физический смысл постоянной С2 — путь, пройденным телом до момента времени t = 0. Если пройденный путь отмерять от того места, где тело находилось в момент t = 0, то С2 = 0. Если и начальная скорость С равна 0, то уравнение движения принимает вид

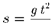точку Мо(жо, Уо-) Уо)? то дифференциальное уравнение

у" = f(x, у, у') (18.3) имеет решение у = у(х) такое, что

у(х0) = уо, у'{хо) = Уо(18-4) Ьсли, кроме того, непрерывны и частные производные — и

ду ду' '

то это решение уравнения единственно.

Геометрический смысл этой теоремы заключается в том, что при выполнении условий теоремы через заданную точку (жо, уо) на координатной плоскости проходит единственная интегральная кривая с заданным угловым коэффициентом у о ее касательной.

Условия (18.4) называются начальными условиями, а задача отыскания решения уравнения (18.3) по заданным начальным условиям (18.4) называется задачей Коши.

Общим решением дифференциального уравнения второго порядка (18.3) называется функция

у = у(х, d, С2),

если она является решением этого уравнения при любых постоянных величинах С и С2, которые могут быть определены единственным образом при заданных начальных условиях (18.4). Частным решением уравнения (18.3) называется общее решение этого уравнения при фиксированных постоянных С и С2у = у(х,СІСІ).

В зависимости от способов решения дифференциальные уравнения второго порядка разделяются на различные типы. Простейшим типом является уравнение

y" = f(x), (18.5)

допускающее понижение порядка. Одно из уравнений этого типа уже было решено в примере 1.

Покажем, как такое уравнение решается в общем случае. Правая часть уравнения (18.5) не содержит функции у и производной у'. Известно, что у" = {у')' = Следовательно, данное

уравнение можно записать так:

\% /<*>.

или

dy' = f{x)dx. Интегрируя последнее уравнение, получим

у = f(x)dx.

f(x) dx^j dx.

Интегрируя еще раз, получим общее решение уравнения (18.5): У =

V Пример 2.

Найти частное решение уравнения

у" = 6 х + sin ж, удовлетворяющее начальным условиям:

у(0) = 2, у'(0) = 3.

Решение. Так как у" = -j-, данное уравнение можно записать так: х

dy' п

—— = Ь х + sin ж,

ах

или

dy' = (6 х + sin х) dx.

Интегрируя, получим

у' = Ъх2 -cosx + d. (18.6)

Тогда

dy = (3 х2 — cos х + Сі) dx.

Интегрируя еще раз, получаем общее решение

у = х3 — sin х + С х + С2Используем начальные условия. Подставив в общее решение х = 0 и у = 2, получим С2 = 2. Подставив в (18.6) х = О и у' = 3, будем иметь

3 = -1 + Сь

откуда

Сі =4.

Следовательно, искомое частное решение, удовлетворяющее заданным начальным условиям, имеет вид

у = х3 — sin х + 4 х + 2.

Геометрически найденное частное решение выражает собой интегральную кривую, которая проходит через точку Mq(0, 2). Кроме того, касательная, проведенная к этой кривой в точке Mq, образует с положительным направлением оси Ох угол, тангенс которого равен 3.

Задача. Найти общее решение уравнения у" = х + cos ж.

Ответ: Xs — cos х + С х + С2. 6

Теорема существования и единственности решения задачи Коїли обобщается и на уравнения более высокого порядка. А именно верна следующая

Теорема 2 (существования и единственности). Если правая часть уравнения

yM = f(x,y,y',...,y^

нерерывна в некоторой окрестности начальной точки

( / (n-i)

(я<ьУо,Уо> ••• ,J/o )

и имеет непрерывные в этой окрестности частные производные у, у ...у(п~1 то оно имеет единственное решение у = у (ж), удовлетворяющее начальным условиям

У = Уо, У = Уо, ••• , Ук } = Уо

При X = Х{).

18.2. Линейное дифференциальное уравнение второго порядка

Линейным дифференциальным уравнением второго порядка называется уравнение вида

(18.7)

где q(x), f(x) — функции переменной х.

Если f(x) ф 0. то уравнение (18.7) называется неоднородным. Если f(x) = 0, то уравнение (18.7) принимает вид

^ + p(x)^ + q(x)y = 0 (18.8)

и называется однородным.

Если в уравнениях (18.7) или (18.8) коэффициенты р(х) и q(x) постоянные, соответственно равные р и то полученные уравнения:

y" + py' + qy = f(x), (18.9)

У" + Р У' + qy = 0 (18.10)

называются линейными дифференциальными уравнениями второго порядка с постоянными коэффициентами.

Теорема 1. Сумма двух решений однородного линейного уравнения (18.8) также есть решение этого уравнения.

□ Предположим, что yi(x) и J/2(#) ~~ решения уравнения (18.8); это означает, что имеют место тождества:

у'{ + р(х)у[ + q(x)y1 = 0,

yf2+p(x)yf2 + q(x)y2 = 0. Складывая почленно эти тождества, получаем

(Уі + Ы" + Р(х) (Уі + Ы' + я(х) (Уі + Ы = о.

Это означает, что функция (у± + у2) удовлетворяет уравнению (18.8). ■

Теорема 2. Если у — решение линейного однородного уравнения (18.8) и если С — произвольная постоянная, то С у также есть решение этого уравнения (18.8).

□ Найдем первую и вторую производные функции С у\

(с1У1у = с1У[, (СіУі)" = сіУ';.

Подставив функцию С у в левую часть уравнения (18.8) и воспользовавшись тем, что

yf{ + p(x)y[ + q(x)y1 = 0,

получим

(Сі У1)" + р(х) (d У1)' + q(x) (Сі У1) =

= Сі у'{ + р(х) Сг у[ + q(x) Сі уі =

= Сг (у'{ + р(х) у[ + q{x) Уі) = Сг ■ 0 = 0.

Это означает, что функция С у удовлетворяет уравнению (18.8). ■

Из двух доказанных теорем вытекает

Следствие. Если у и уі — решения линейного однородного уравнения (18.8), то Су и С2У2 — решения этого уравнения, следовательно, и выражение

У = Сг у + С2 У2

есть решение этого уравнения.

В дальнейшем нам понадобятся понятия линейной зависимости и независимости функций.

Две функции у и у2 называются линейно зависимыми, если

У о „

их отношение — является постоянной величиной. В противном Уі

случае функции у и у2 называются линейно независимыми.

Например, функции у = х, у2 = Зж линейно зависимы, а функции уі = х, у2 = х + 1 линейно независимы.

От того, линейно зависимы или линейно независимы функции у и у2, зависит ответ на вопрос: является ли функция у = = С у + С2 У2 общим решением уравнения (18.8)?

Верна следующая

Теорема 3. Если у и у2 — линейно независимые решения линейного однородного дифференциального уравнения (18.8), то функция

Уот = Сі уі + С2 У2

является общим решением этого уравнения.

V Пример. Найти общее решение уравнения у"-3у' + 2у = 0,

если известно, что уі = ех и у2 = е2х — частные решения этого уравнения.

Решение. Данное уравнение является линейным однородным. Так как

У* ^1 ^

Уі ех

не является постоянным числом, то эти решения являются линейно независимыми. Поэтому

у{х) = С1ех + С2е2ж,

где С и С2 — произвольные постоянные, является общим решением уравнения. А

Что касается решения неоднородного уравнения (18.7), то имеет место следующая

Теорема 4. Общее решение уравнения (18.7) равно сумме общего решения соответствующего однородного уравнения (18.8) и какого-нибудь частного решения данного уравнения (18.7). Если

У от = Сі Уі (х) + С2 У2(х)

есть общее решение уравнения (18.8), а у есть какое-нибудь частное решение неоднородного уравнения (18.7), то

у = Сі г/i(ж) + С2у2(х) + у

есть общее решение неоднородного уравнения (18.7).

Таким образом, чтобы найти общее решение линейного неоднородного уравнения второго порядка, надо предварительно найти общее решение соответствующего уравнения без правой части и прибавить к нему какое-нибудь частное решение заданного уравнения.

С другой стороны, чтобы найти общее решение однородного уравнения, надо иметь два частных линейно независимых решения этого уравнения. Для случая, когда р(х) и q(x) не являются постоянными числами, нахождение таких частных решений — весьма сложная задача. Сравнительно легко найти такие решения, когда р и q — постоянные числа.

18.3. Линейные однородные уравнения второго порядка с постоянными коэффициентами

Общим решением линейного однородного уравнения с постоянными коэффициентами (18.10) является функция

у = С1у1 + С2У2,

где у и у2 — два линейно независимых частных решения этого уравнения.

Для нахождения одного из частных решений поступим следующим образом. Предположим, что

У = екх,

где к — некоторое постоянное число, есть решение уравнения (18.10). Выясним, при каких значениях к показательная функция у = екх станет решением уравнения (18.10). Для этого находим

у' = кекх, у" = к2екх

и подставляем у, у' и у" в левую часть уравнения (18.10). В результате подстановки получим выражение

к2екх +ркекх + qekx = екх (k2+pk + q). (18.11)

Чтобы у = екх удовлетворяло уравнению (18.10), требуется, чтобы выражение (18.11) было тождественно равно нулю. Так как сомножитель екх не равен нулю ни при каком значении к, то второй сомножитель должен быть равен нулю. Следовательно, те значения к, которые удовлетворяют уравнению

k2+pk + q = 0, (18.12)

пригодны для составления частного решения у = екх.

Уравнение (18.12) называется характеристическим по отношению к уравнению (18.10).

Как видно, чтобы получить характеристическое уравнение (18.12), достаточно заменить в данном уравнении (18.10) производные соответствующими степенями неизвестной к.

Если действительное число к является корнем характеристического уравнения, то, как было показано, ек х — частное решение уравнения (18.10). Поиск другого частного решения, линейно независимого с первым, зависит от вида характеристического уравнения.

При решении характеристического уравнения могут встретиться три случая: корни характеристического уравнения действительные и различные, корни равные, нет действительных корней. Справедлива следующая

Теорема. 1. Пусть характеристическое уравнение (18.12) уравнения (18.10) имеет действительные корни к и к2, причем к ф к2. Тогда обилие решение уравнения (18.10) имеет вид

у = Сгек1Х + С2ек2Х,

где С и С2 — некоторые числа.

Если характеристическое уравнение (18.12) имеет только один корень к, то общее решение уравнения (18.10) имеет вид

у = С1екх + С2хекх,

где С и С2 — некоторые числа.

Если характеристическое уравнение (18.12) не имеет действительных корней, то общее решение уравнения (18.10) имеет вид

у = Сі еах smfix + С2 еах cos/Зж,

где а = —р/2, /3 = /q — р2/4 , С и С2 — некоторые числа.

□ Пусть корни характеристического уравнения (18.12) действительные и различные, т. е. кф к2. Тогда

У1 = eklX и у2 = ек2Х

являются линейно независимыми решениями, так как они удовлетворяют уравнению и

Уі ekl

Отсюда и из теоремы 3 п. 18.2 следует, что общее решение уравнения (18.10) имеет вид

у = deklX + С2ек2Х.

Таким образом, для случая, когда характеристическое уравнение имеет два действительных корня, теорема доказана.

Для двух других случаев теорема доказывается аналогично. ■

Ниже приведены применения доказанной теоремы к известной задаче о малых колебаниях пружинного маятника. Эти примеры приводятся здесь не случайно. Соответствующая физическая задача может быть интерпретирована как экономическая задача о колебаниях цен.

V Пример 1. Материальная точка массы т, движущаяся вдоль прямой, притягивается к неподвижному центру О с силой, пропорциональной удалению s точки от притягивающего центра (упругая сила). Найти закон движения этой точки (пренебрегая сопротивлением среды).

Решение. Согласно закону Ньютона имеем

їїі а = f.

т —т = —b s,

Ї J.Z 7

Здесь через т обозначена масса точки, через а — ускорение, через F — сила. Закон Ньютона в условиях нашей задачи можно записать в следущей форме:

d?s

dt2

где b — коэффициент пропорциональности и знак минус поставлен потому, что направление действующей силы обратно по знаку смещению s. Отсюда

d2s , 2 п

dt

Ъ

где и V т

Это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами р = 0 и q = и2. Соответствующее характеристическое уравнение

к2 + и2 = 0

не имеет действительных корней. Общее решение уравнения согласно теореме имеет вид

s = deat smf3t + C2eat cos/3t.

Поскольку

а = -р/2 = 0, р = у/д-р?/4=ш,

ТО

s = s(t) = С sin 00 t + С2 cos UJ t.

Можно положить

С = A sin ф, С2 = A cos ф,

где Л и ф — некоторые другие произвольные постоянные. Отсюда, используя тригонометрические формулы, получаем

s(t) = A sin (00 t + ф) ,

или

s(t) = Asm +

т. е. материальная точка в наших условиях совершает периодические гармонические колебания около притягивающего центра с амплитудой А и начальной фазой ф. А

V Пример 2. Материальная точка массы т, движущаяся вдоль прямой, притягивается к неподвижному центру О с силой, пропорциональной удалению s точки от притягивающего центра (упругая сила). Найти закон движения этой точки с учетом сопротивлением среды.

Решение. В отличие от предыдущего примера, помимо «упругой» силы

F= -bs

на точку массы т действует еще и сила сопротивления среды. Обычно полагают, что сила сопротивления по величине проds

порциональна скорости — и направлена в противоположную

сторону {^F = —г Поэтому уравнение отклонения точки от неподвижного центра О имеет вид

т а = F + F

или

d2s ds .

т —7Т = —г — bs,

dt2 dt

где г — постоянная сопротивления среды.

Это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, которое в привычной форме записывается так:

Соответствующее характеристическое уравнение имеет вид

т т

Поведение решения однородного дифференциального уравнения зависит от дискриминанта характеристического уравнения. Возможны три случая: дискриминант D больше нуля; дискриминант равен нулю; дискриминант меньше нуля. 1. Если дискриминант

т) т

то характеристическое уравнение имеет два различных действительных корня

г 1 ( г2 46 _ г 1 ( г2 46

s(t) = C1eklt + C2ek2t =

= Є 2т І Є + Є

2. Если дискриминант

г 2 46

D= - — = 0, то характеристическое уравнение только один корень

2 771

который является действительным числом, и

s{t) = Сг ekt + С21 ek * = e~^d (Сі + C2 «) • 3. Если дискриминант

D = (£)2-l^<o,

то характеристическое уравнение не имеет действительных корней и

s(t) = Сгеаі sin $ t + C2eat cos fit.

Поскольку

то

1 2 1 т т I

1 /46 /гх2

+ C2COS-W— - - * .

2 у ш ш у

Чтобы проанализировать закон движения точки, введем новые обозначения. Обозначим г/{2т) через 5, а Jbjm — через cjg. Коэффициент 8 называют коэффициентом затухания, a cjo — циклической частотой свободных колебаний в отсутствии трения.

В новых обозначениях уравнение колебаний имеет вид

s"{t) + 26s'{t) + uls{t) = 0.

Обобщая предыдущие рассуждения получаем, что для движения точки возможны три случая:

1. Если 8 > cjo, то имеет место непериодическое затухание:

s(t)

Функция s(t) монотонно убывает с ростом t. Система, выведенная из состояния равновесия, асимптотически, т. е. при t —> оо, возвращается в это состояние.

2. Если 8 = cjo, то также имеет место непериодическое затухание:

s(t) = e-st(C1 +C2t).

3. Если 8 < cjo, то система совершает затухающие колебания:

s(t) = A0e~st sm(ut + фо),

где Aq и фо — постоянные величины, оо = ^JoJq — 82 — собственная

циклическая частота колебаний. Величина A(t) = Aq е~^г называется амплитудой затухающих колебаний. А

Колебания рыночных цен. Примеры 1 и 2 применимы не только к колебаниям пружинного маятника. Рассмотренное дифференциальное уравнение применимо к любой системе, испытывающей колебания. Например, оно может быть интерпретировано и как уравнение колебаний отклонения рыночной цены товара от его естественной цены. Более точно эта интерпретация выглядит следующим образом. Пусть s(t) — отклонение рыночной цены от ее естественного значения в момент времени t (при s(t) = О рыночная цена в момент времени t совпадает с равновесной). Найдем уравнение отклонения рыночной цены от ее естественного состояния. Для этого предположим, что на рынке товаров действуют две силы, аналогичные силам упругости и сопротивления для пружинного маятника, которые условно назовем силой (тяготения) Смита и силой сохранения. Чтобы пояснить, что понимается под силой Смита, приведем две его цитаты:

«Фактическая цена, за которую обычно продается товар, называется его рыночной ценой. Она может или превышать его естественную цену, или быть ниже ее, или же в точности совпадать с нею ... Таким образом, естественная цена как бы представляет собой центральную цену, к которой постоянно тяготеют цены всех товаров. Различные случайные обстоятельства могут иногда держать их на значительно более высоком уровне и иногда несколько понижать их по сравнению с нею. Но каковы бы ни были препятствия, которые отклоняют цены от их устойчивого центра, они постоянно тяготеют к нему 1) .»

Описанное в этих цитатах «тяготение» (в чем-то схожее с силой упругости пружины) будем называть силой Смита F(t). Естественно предполагать, что сила Смита направлена в сторону точки О на оси Os и по по величине пропорциональна отклонению цены s(t):

F1(t) = -bs(t).

Коэффициент пропорциональности b будем называть коэффициентом Смита.

Помимо силы Смита на рынке может действовать еще и аналог силы трения, которую мы назовем силой сохранения F2(t). Адам Смит писал: «Одно и то же число рабочих в сельском хозяйстве производит в различные годы весьма различные количества зерна, вина, масла, хмеля и т. п., между тем как одно и то же количество прядильщиков и ткачей каждый год производит

г) Смит Л. Исследование о природе и причинах Богатства народов. Книга первая. М.: Ось-89, 1997. С. 56, 58.

одинаковое или почти одинаковое количество полотна и сукна ... Собственный опыт каждого человека говорит ему, что цена полотна или сукна не подвержена столь частым и столь большим колебаниям, как цена хлеба. Цена одного рода товаров изменяется лишь в зависимости от изменений в спросе; цена другого рода товаров изменяется не только в зависимости от изменений в спросе, но и в зависимости от гораздо больших и гораздо более частых колебаний количества товара, доставляемого на рынок для удовлетворения этого спроса 1) .»

Таким образом, сила сохранения тем больше, чем более реже происходят колебания цены. Эта сила зависит от вида товара (сезонных и других колебаний количества товаров на рынке), психологии продавца (меньшей или большей склонности к изменению цены) и других факторов. Естественно полагать, что сила

сохранения по величине пропорциональна скорости — и направ-

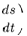
будем называть коэффициентом сохранения. Используя закон Ньютона

т а = F + F2

и аналогию с пружинным маятником, получаем дифференциальное уравнение отклонения s(t) рыночной цены товара от ее естественной цены:

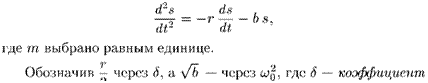затухания, а ооо — циклическая частота свободных колебаний в отсутствии силы сохранения.

В новых обозначениях уравнение колебаний имеет вид

s"(t) + 28s'(t) + ujls(t) = 0.

По аналогии с пружинным маятником получаем, что возможны три случая:

1. Если 8 > cjq, то имеет место непериодическое затухание:

s(t) = de

+ С2е

г) Там же, с. 58-59.

Функция s(t) монотонно убывает с ростом t. Система, выведенная из состояния равновесия, асимптотически, т. е. при t —> оо, возвращается в это состояние.

Если 6 = cjo, то также имеет место непериодическое затухание:

s(t) = e-st (Сі +C2t).

Если 0 < 6 < cjo, то система совершает затухающие колебания:

s(t) = A0e~6t sin(cj t + фо),

где Л о и фо — постоянные величины, а оо = ^oJq — S2 — собственная циклическая частота колебаний. А

V Пример 3. Найти общие решения уравнений:

а) у" + 22/,-15у = 0;

б) у"-10у' + 25у = 0;

в) у" -4у' + 13у = 0.

Решение.

а) Составляем характеристическое уравнение

к2 + 2 к -15 = 0.

Корнями этого уравнения являются два действительных числа к = —5 и к2 = 3. Поэтому общее решение имеет вид

у = СіЄ"5ж + С2е3ж.

б) Составляем характеристическое уравнение

к2 -10 к + 25 = 0.

Решая это уравнение, получим к = к2 = 5. Так как корни равные, то общее решение

у = (С1 + С2х)е5х.

в) Характеристическое уравнение

fc2-4fc + 13 = 0

не имеет действительных корней. Вычисляем соответствующие а и /3:

а = -р/2 = 4/2 = 2, /3 = р2/4 = Дз 16/4 = 3.

Отсюда получаем общее решение:

у = е2 х (Ci cos 3 х + С2 sin 3 х). А

Задача 1. Найти общие решения уравнений: а) у" + 2у, + 2у = 0;

б) у" + 4у = 0;

в) у" + 4у' + 4у = 0.

Ответ:

а) у = е~х (Сі cos ж + С2 sin ж). Если х — время, то эта

функция описывает колебания отклонений у рыночной цены от

ее естественного значения. Колебания являются затухающими.

При х —> оо отклонение от естественной цены стремится к нулю;

б) у = С cos 2 ж + С2 sin 2 ж. Функция описывает колебания

отклонений рыночной цены от ее естественного значения

в момент времени х. Колебания являются незатухающими.

При х —> оо отклонение у(х) не имеет предела. Рыночная цена

постоянно колеблется вокруг естественной цены;

в) у = (Сі + С2 х) е~2х. Функция описывает постепенное понижение рыночной цены. При х —> оо отклонение от естественной

цены стремится к нулю.

V Пример 4. Найти частное решение уравнения ^ + 4^ + 4^ = 0, удовлетворяющее начальным условиям

у(0) = 4, у'(0) = 0. Решение. Общее решение искомого уравнения имеет вид у = (С1 + С2х)е-2х.

Воспользуемся начальными условиями для определения произвольных постоянных С и С2. Находим производную общего решения:

у1 = -2 Сі е~2х + С2 е~2х 2 С2 х е~2х.

Подставив х = 0иу = 4в общее решение, получим С = 4. Подставив х = 0иу' = 0в найденное выражение для у' получим

0 = 2Ci + C2,

откуда С2 = 8.

13 Я. М. Ахтямов

Следовательно,

у = 4е-2х + 8хе-2х

есть искомое частное решение, удовлетворяющее заданным начальным условиям. А

Задача 2. Найти частное решение уравнения

у"-5у' = 0,

удовлетворяющее начальным условиям

3,(0) = 1, у'(0) = -5.

Ответ: у = 2 — е~5ж.

18.4. Линейные неоднородные второго порядка с постоянными коэффициентами

Пусть требуется найти общее решение линейного неоднородного уравнения второго порядка с постоянными коэффициентами

у" + РУГ + ЯУ = f{x).

(18.13)

Напомним, что общее решение неоднородного уравнения (18.13) равно сумме общего решения соответствующего однородного уравнения

у" + ру' + qy = О

(18.14)

и какого-нибудь частного решения неоднородного уравнения (18.13). Если

Уоди = Сі уі(х) + С2у2(х)

есть общее решение уравнения (18.14), а у — какое-нибудь частное решение неоднородного уравнения (18.13), то общее решение выражается формулой

У = УоАн + У.

(18.15)

Метод неопределенных коэффициентов. В предыдущем параграфе рассмотрен способ нахождения общего решения уравнения (18.14). Следовательно, остается указать способ нахождения какого-либо частного решения заданного уравнения (18.13). Рассмотрим способ отыскания частного решения методом неопределенных коэффициентов. Этим методом можно пользоваться в нескольких случаях. Рассмотрим случай, когда функция f(x) из правой части (18.13) представляется в виде

f(x) = emxPn(x),

где Рп(х) — многочлен п-й степени.

Теорема 1. Если т не является корнем характеристического уравнения

k2 +рк + q = О, то частное решение уравнения (18.13) имеет вид

y = emxQn(x),

где Qn(x) — многочлен п-й степени с неопределенными коэффициентами.

Если т — корень характеристического уравнения k2 +рк + q = О, то частное решение уравнения (18.13) имеет вид

y = xremxQn(x),

где г = 1 или 2, смотря по тому, совпадает т с одним из корней характеристического уравнения или же с каждым из двух равных корней характеристического уравнения.

V Пример 1. Найти общее решение уравнения

у"-7у' + Юу = 4е3я

Решение. Находим общее решение уравнения без правой части

^-7^ + 10 = 0.

Характеристическое уравнение

к2 -7 к + 10 = 0

имеет корни &1 = 2 и &2 = 5.

Общее решение однородного уравнения таково:

УоД„ = Сі е2х + С2е5х.

Рп{х) — 4 — многочлен нулевой степени, т = 3 не совпадает ни с одним из из корней характеристического уравнения. Поэтому частное решение у следует искать в виде А е3 ж, т. е.

У = Ае3х,

где А — неопределенный коэффициент, который нужно найти. Дифференцируя это равенство, находим:

^ = ЗЛе3ж, у" = 9Ле3ж.

Подставим у, у1 и у" в левую часть исходного уравнения и определим значение коэффициента А:

9 А е3ж 21 А е3ж + 10 А е3ж = 4 е3ж;

-2 Л = 4; Л = -2.

Следовательно, частное решение у = Л е3ж = —2 е3ж, а общее решение

у = СіЄ2х + С2е5ж -2е3ж. А

V Пример 2. Найти общее решение уравнения у" у' -6у = 12х2-2х + 1.

Решение. Находим общее решение однородного уравнения y"-y'-Qy = 0. Так как характеристическое уравнение

к2 к 6 = 0

имеет корни &1 = —2 и &2 = 3, то общее решение однородного уравнения

у0ДИ = Сге-2х + С2е3х.

В правой части заданного уравнения ешж = е°'ж = 1, поэтому m = 0. Число нуль не является корнем характеристического уравнения. Следовательно, частное решение у заданного уравнения следует искать в виде многочлена второй степени, т. е.

у = Ах2 + В х + С.

Дифференцируя это равенство, находим у1 иуП:

у' = 2Ах + В; у" = 2А.

Подставив у, у1 и у11 в левую часть заданного уравнения, получим равенство:

2 А-2 АхВ -6 Ах2 -бВх-бС = 12 ж2 2 ж + 1,

или

-6 А х2 + (-2 А 6 В) х + (2 А В 6 С) = 12 ж2 2 ж + 1.

Выбираем неопределенные коэффициенты Л, 5 и С так, чтобы последнее равенство стало тождеством. Для этого приравниваем коэффициенты при одинаковых степенях переменной х. В результате получаем систему трех уравнений с тремя неизвестными А, В и С.

Решая систему

'-6 А = 12,

< -2А-6В = -2,

,2А-Я-6С = 1,

находим, что А = —2, В = 1, С = — 1. Следовательно, частное решение имеет вид

у = -2х2 + х-1,

а общее —

у = Сг е~2х + С2 е3ж 2х2 + х 1. А

V Пример 3. Найти общее решение уравнения у"-2у' + у = хех.

Решение. Характеристическое уравнение k2-2k + l = 0 однородного уравнения имеет двойной корень

к = к2 = 1.

Поскольку

f(x) = хех

и т = 1 совпадает с корнем характеристического уравнения, а Рп(х) — многочлен первой степени, то частное решение заданного уравнения есть функция

у = х2 ех (А х + В) = ех (A Xs + В х2).

Вычислим у' и у":

у' = ех {А ж3 + В ж2) + ех (3 А ж2 + 2 В ж) =

= ех (А ж3 + В х2 + З А Xі + 2 В ж); у " = ех (А ж3 + В х2 + 3 А х2 + 2 В ж)+

+ еж(ЗЛж2 + 2£ж + 6Лж + 2£) =

= ех (А ж3 + {В + 6 А) х2 + (4 В + 6 А) х + 2 В).

Подставляя эти значения в исходное неоднородное дифференциальное уравнение, получим

ех (А ж3 + (В + 6 А) х2 + (4 В + 6 А) х + 2 В)2 ех {А ж3 + В х2 + 3 А ж2 + 2 Б ж) + ех (А ж3 + В ж2) = ж еж, откуда

Лж3 + Бж2 + 6Лж2 + 4Вж + 6Лж + 2В-2Л ж3-2Вж2-6Лж2-4Вж + Лж3 + Вж2 = ж;

сократив, имеем

6Лж + 2Б = ж,

т. е.

6Л = 1, 2£ = 0,

откуда

Л = 1/6, в = о.

Подставляя эти значения в частное решение, получим:

у = ж3 ех. у 6

Поскольку общее решение однородного уравнения есть функция Уот = (Ci + C2x) ех,

общее решение неоднородного дифференциального уравнения есть функция

у = {Ci + C2x)ex + хъ ех. ▲

V Пример 4. Найти частное решение уравнения у"-у'-2у = 9е2х, удовлетворяющие начальным условиям

у(0) = 2, у'(0) = 13.

Решение. Находим общее решение однородного уравнения у"-у'-2у = 0.

Характеристическое уравнение

к2 -к-2 = 0

имеет два корня:

&1 = -1, к2 = 2.

Отсюда

у 0ДН = С1е-х + С2е2х.

Так как в правой части заданного уравнения Рп(х) = 9х2х и т = 2 совпадает с одним из корней характеристического уравнения, то частное решение у следует искать в виде функции Ах е2х.

Дифференцируя дважды у = А х е2ж, получим:

у' = Ае2х + 2Ахе2ху" = 2Ае2х + 2Ае2х +4Ахе2х.

Подставим у, у1 и у11 в левую часть заданного уравнения и определим коэффициент А :

4Ле2ж +4Ахе2х Ае2х -2Ахе2х -2Ахе2х = 9е2х;

ЗЛ = 9; А = 3.

Следовательно, частное решение имеет вид

у = Ъхе2х,

а общее решение:

У = 2/одн + у = Сі е~х + С2 е2х + 3х е2х.

Используя начальные условия , определим значения произвольных постоянных С и С2Дифференцируя общее решение, получим:

у' = -Сі е~х + 2 С2 е2х + 3 е2х + 6 х е2х. (18.16)

Подставив в общее решение х = 0 и у = 2, будем иметь:

2 = Сх + С2. Подставив х = 0 и у1 = 13 в (18.16), будем иметь:

13 = -Сг + 2 С2 + 3; 10 = -Сг + 2 С2. Решая систему

Сг + С2 = 2,

-Ci + 2C2 = 10,

находим: С — —2 и С2 = 4. Таким образом,

у = -2е~х + 4е2ж + 3же2ж

есть частное решение, которое удовлетворяет заданным начальным условиям. А

Задача 1. Найти общее решение уравнения у"-5у' + 6у = (12х-7)е~х.

Ответ: у = С е2х + С2 е3ж + х е~х.

Задача 2. Найти общее решение уравнения у" + 3у + 2у = 2х2-4х-17.

Ответ: у — С е~х + С2 е~2х + х2 5 х 2. Задача 3. Найти частное решение уравнения у" + 4у = 8х, удовлетворяющее начальным условиям:

у(0) = 0; у'(0) = 4.

Ответ: у = sm2x + 2x.

Метод неопределенных коэффициентов применим только в тех случаях, когда правая часть линейного неоднородного дифференциального уравнения, т. е. функция /(ж), является либо многочленом, либо показательной функцией, либо синусом или косинусом (этот случай нами не рассматривался), либо произведением этих функций. В тех случаях, когда правая часть f(x) отлична от названных выше функций, применяют так называемый метод вариации произвольных постоянных.

Метод вариации произвольных постоянных. Метод вариации произвольных постоянных является общим методом, позволяющим решать неоднородные дифференциальные уравнения с постоянными коэффициентами.

Сущность метода заключается в следующем.

Рассмотрим линейное неоднородное уравнение 2-го порядка с постоянными коэффициентами (18.13). Пусть общим решением соответствующего однородного уравнения (18.14) будет функция

Уодн = С1У1(х) + С2у2(х), (18.17)

где yi(x) и у2(х) — два линейно независимых частных решения однородного уравнения (18.14), а С и С2 — некоторые произвольные постоянные. Заменим в общем решении (18.17) постоянные С и С2 некоторыми функциями С(х) и С2(х) так, чтобы

У = С1(х)у1(х) + С2(х)у2(х) (18.18)

стало решением неоднородного уравнения (18.13). Другими словами, будем искать частное решение уравнения (18.13) в виде (18.18), т. е. в виде копии функции (18.17), в которой осуществлена вариация (видоизменение) произвольных постоянных произвольными функциями.

Найдем условия на функции С\{х) и С2(х), при которых (18.18) становится решением неоднородного уравнения (18.13).

Если у есть решение неоднородного уравнения (18.13), то при подстановке в левую часть этого уравнения у, у1 иуП получим тождество.

Дифференцируя (18.18), имеем

у' = С[(х) У1(х) + d(x) у[(х) + С2(х) У2(х) + С2(х) у'2(х), или

у' = [С[(х) У1(х) + С'2{х) у2{х)} + Ci(x) у[(х) + С2(х) у'2(х).

Выберем функции Сі (ж) и С2(х) так, чтобы сумма в квадратных скобках была равна нулю, т. е., чтобы имело место равенство

С[(х)У1(х) + С2(х)У2(х) = 0. (18.19)

Тогда

у' = С1(х)у[(х) + С2(х)у'2(х). Дифференцируя еще раз, находим у":

У" = С[(х) у[(х) + Сі(х) у'Цх) + С'2{х) у'2(х) + С2(х) у'2х).

Подставив у, у1 и у11 в левую часть неоднородного уравнения (18.13), получим

С[(х) у[(х) + Сг(х) у'{{х) + С'2{х) у'2(х)+

+ С2(х) у'Цх) + р d(x) у[(х) + р С2(х) у'2{х)+

+ q Ci(x) yi(x) + qC2(x)y2(x) = f(x). Или, группируя члены, получим:

d(x) [у"(х)+ру[(х) + ЯУ1(х)] +

+ С2(х) [y2,{x)+py'2{x) + qy2{x)] +

+ C1(x)y,1(x) + C2(x)y'2(x) = f(x).

Так как у\{х) и у2(х) являются решениями однородного уравнения (18.14), то выражения в квадратных скобках равны нулю. Следовательно,

С[(х) у'г(х) + С'2{х) у'2(х) = f(x). (18.20)

Итак, для нахождения неизвестных функций С±(х) и С2(х) надо решить совместно систему уравнений (18.19) и (18.20).

Таким образом, метод вариации произвольных постоянных отыскания частного решения неоднородного решения состоит из двух этапов:

На первом этапе находятся неизвестные функции С{(ж) и С2(х) из системы уравнений (18.19) и (18.20):

С[(х)У1(х) + С2(х)у2(х) = 0, C[(x)y'1(x) + C^x)y'2(x) = f(x).

На втором этапе по найденным функциям С{(ж) и С'2(х) с помощью интегрирования отыскивают С(х) и С2(х) и подставляют в представление для частного решения

у = Сі (ж) г/1 (ж) + С2(ж) у2(х).

V Пример 5. Найти общее решение уравнения

к2+ 1 = 0.

Решение. Характеристическое уравнение имеет вид Следовательно,

а = 0, /3 = 1.

Поэтому частными решениями однородного уравнения

у" + У = о

являются функции

У = COS Ж, У2 = Sin Ж,

а общее решение однородного уравнения есть функция

У одн = С cos х + С2 sin ж. Таким образом, частное решение заданного уравнения имеет вид

у = Сі (ж) cos х + С2(х) sin ж, где функции С\{х) и С2(х) находятся из системы уравнений 'С[(х) cosх + С'2(х) sinх = О,

-С{(ж) sin ж + С^ж) cos х = —^

sin X

Умножая первое уравнение этой системы на sin ж, а второе на cos х и суммируя их, получаем

С'2(х) sin2 х + С'2(х) cos2 х =

sin X т. е.

С2Х) = •

sin X

Интегрируя находим

С2(х) = In | sin х

(здесь не пишем In | sin х + С, так как ищется не общее, а частное решение. Поэтому можно считать, что С = 0). Подставляя

С2х) =

sin X

в первое из уравнений данной системы, получаем С[(х) cos х + cos х = 0,

откуда

С[(х) = -1.

Следовательно,

С(х) = —х.

Таким образом, частное решение заданного дифференциального уравнения представляет функцию

у = —х cos х + sin х In I sin xI, а общее решение — функцию

у = (Сі — х) cos х + (С2 + In I sin x) sin X. A Задача 4. Найти общее решение уравнения

Ответ:

у = (Сі — In I sin x) cos x + (C2 — ^ ctg x — x) sin X.

Задача 5. Найти общее решение уравнения у" + Ay' + Ау = е~2х In ж.

Ответ:

у= (с1 + С2х + ±х2 Ых-^х2^ е~2х.

Принцип наложения. При решении неоднородных уравнений часто оказывается полезным принцип наложения (или принцип суперпозиции.)

Теорема 2. Если правая часть линейного неоднородного урав-нения представлена в виде суммы двух функций, т. е. дано уравнение

у" + ру' + qy = Д(ж) + f2(x) и уї есть частное решение уравнения

у" + ру' + qy = /і(ж), а у2 есть частное решение уравнения

у" + ру' + qy = /2(ж), то у = уї + у2 есть частное решение заданного уравнения.

V Пример 6. Найти общее решение уравнения у" 7 у' + 10 у = 4 е3х + 10 х + 3.

Решение. В данном случае f(x) = 4е3ж, a f2(х) = 10х + 3. Ранее в примере 1 (с. 387) уже было найдено общее решение неоднородного уравнения

у"-7у' + 10у = 4е3х.

Общим решением этого неоднородного уравнения с правой частью fi(x) является

y = d е2ж + С2е5ж-2е3ж.

Частным решением уравнения

у"-7у' + 10у = 10х + 3

с правой частью f2(x) является функция

У2 = х + 1 •

Следовательно, согласно теореме 2, общее решение исходного уравнения таково:

у = С1е2х + С2е*х-2е3х+х + 1. А

Задача 6. Найти общее решение уравнения у"-Zy' + 2у = Ъе2х + 2х2.

Ответ:

у = Сг е2х + С2 ех + 3 х е2х + х2 + 3 х + 7-.

Колебания цен. В предыдущем параграфе рассматривалось однородное уравнение колебаний цен

s"(t) + 28sf(t) + uls(t) = 0,

где s(t) рассматривалось как отклонение рыночной цены от своего «естественного» значения. Экономический смысл имеет также и неоднородное уравнение

s"(t) + 28s'(t) + ou2s(t) = f(t).

Оно описывает колебание цен на рынке при внешнем воздействии f(t). Внешнее воздействие может быть интерпретировано, например, как завоз на рынок большой партии аналогичной импортной продукции или же как государственные дотации и т. п.