§ 2.1. операции над матрицами
§ 2.1. операции над матрицами
Определение 1. Матрицей (точнее, числовой матрицей) называется прямоугольная таблица, составленная из чисел. Размером матрицы называется пара чисел т, п, где т — число строк, an — число столбцов в таблице.
Например,
Однако главные применения матриц связаны с другой операцией — умножением матриц. Это очень своеобразная операция, лежащая в основе целого раздела линейной алгебры — алгебры матриц.
размера т х и; -размера пхк.
Пусть даны две матрицы:
А-В-
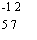 матрица размера 2x3.
матрица размера 2x3.
Числа, составляющие матрицу, называются ее элементами.
R
'(Л 1 2
V4,
Матрица размера п х п называется квадратной матрицей порядка и. Матрицу размера 1 х п (одна строка) называют обычно матрицей-строкой, а размера т х 1 (один столбец) — матрицей-столбцом. Матрица-строка 1 х п — это фактически вектор из R", а матрица т х 1 — вектор из R™. Например,
(-1, 2, 7) Є R ,
т
Как видно, число столбцов в матрице А по условию равно числу строк в матрице В, или, выражаясь свободнее, длина строки в матрице А совпадает с высотой столбца в матрице В. В этом случае можно определить матрицу С АВ, которая будет иметь
. Элемент матразмеры т х к ^правило для запоминания: ™ • ^ = ^
рицы С, расположенный в произвольной j-ой строке (i = 1 т)
и произвольном j-ом столбце (J = 1, к), по определению равен скалярному произведению двух векторов: і-ой строки матрицы А иу-го столбца матрицы В.
Например:
О
Для сокращенной записи матриц будем использовать заглавные буквы: А, В,.... Например, А=~^ ^ 3 ]или, скажем, В =
О
V J
О 0 6 5 II 8
-2 3 4 2
Над матрицами можно производить ряд операций. Прежде всего матрицы одинакового размера можно складывать. Сложить две матрицы означает сложить их элементы, стоящие на одинаковых местах. Например,
-1 2 з"! 5 7 6
3 -2 1 4
1 1 1 2 і -1
і 2
г2 1
1 ,
V J
3^ 2
6 , J
' 3 • 0 + (-2) • 0 10 + 40
З •(-!) +(-2)-2^ 1 • (-1) + 4-2
1 ■ 2 + 1 • 1 + (-3) • 1) 1 2 + 2-1 +41
— произведение не существует, так как длина строки в матрице А, равная 2, не совпадает с высотой столбца в матрице В, равной 3.
А =
Соглашение. Элементы матрицы в общих рассуждениях принято обозначать буквами с двумя номерами (индексами). Если, например, матрица обозначена А, то ее элемент, расположенный в /-ой строке и 7-ом столбце, обозначается а^. Скажем,
'II "12 "13 !21 а22 а23
Пусть А, В, С — квадратные матрицы одного и того же размера, скажем, 2x2. Запишем их так:
| (а, а2) | (с г | ||||
| — | 1 L | ; В = | ; с = | 1 L | |
| аг а. |
Имеем:
— общая запись матрицы размера 2x3.
С = АВ:
В таких обозначениях правило умножения матриц запишется следующим образом:
Су = ап-Ьь+ аа-Ьу+...+ аіп-ЬпҐ
з L4
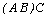
а3^1 + a4tb3 a3b2 + aAb^
Ґ(axb{ + а2Ь3) c,.+ (Д|Ь2 +12^4) c3 (axb{ + a2b3) c2 + (a]b2 + a2b4) c4 (а3й, + <з4&3) c, + (a3fo2 +a4b4) c3 (a36, + a4b3) c2 + (а3Ь2 + а4Ь4) c4
Свойства умножения матриц
Умножение матриц в некоторых отношениях сходно, но в других отношениях отличается от умножения чисел.
.аЬ = Ьа для чисел, но АВ * В А (в общем случае) для матриц.
2 О 1 5
-1 2Ї 3 7
2 О 1 5
Например,
-I 2^ 3 7
О 10 ї 13 35
но
-1 2 3 7
-1 2 3 7
-2 4 14 37
не существует.
2. Важнейшее свойство умножения матриц заключается в том, что умножение матриц, подобно умножению чисел, подчиняется
сочетательному закону:
(АВ)С = А(ВС).
Доказательство в общем виде требует довольно громоздких записей, поэтому ограничимся только случаем квадратных матриц.
34
a a:
A{BC) =
■3 u4
Ь jС j -*£>2C3 ^1C2 + ^2C4
^3c,+fc4c3 63c2 + ft4c4
'а^с, + ft2c3) + a2(*3ci +^4сз) ^(ft^ + ^c^ + a^ft^ + ^c,,)4 a^c, +fc2c3) + a4(b3C| + b4c3) a3(fc,c2 + + a4(fo3c2 + b4c4)^ '
Сравнивая полученные выражения для матриц {АВ)С и А(ВС), убеждаемся в их полном совпадении. Например, элемент матрицы (АВ)С, расположенный в первой строке и втором столбце, равен
alblc2 + alb2c4 + а2Ьгс2 + a2b4c4,
но точно такое же выражение имеет и элемент матрицы А(ВС), расположенный в том же месте.
3. Любой матрице А размера тхи можно сопоставить матрицу А (читается:матрица,транспонированнаяк/4)размералхт.Строки матрицы Ат — это столбцы матрицы А с сохранением их порядка.
Например,
f 3 \ -2 6 7 5
J
Предоставляем читателю проверить следующее свойство умножения матриц самостоятельно:
(АВ)Т = ВТ-АТ.
Пример. Предприятие выпускает три вида продукции Пх, П2, /73, используя два вида сырья Slt S2. Нормы расхода сырья характеризуются матрицей
Я, п2 пъ
А = § 2.2. Матричная запись системы линейных уравнений
Х| + а
Mi
и12
Одно из важных применений матриц связано с рассмотрением систем линейных уравнений. Пусть дана система mxn:
х2 +... + а,
(Буквы Si,S2,nl,n2,n3 представлены для пояснения. Например, число а21 = 3 в матрице А означает, что на выпуск единицы продукции /7, расходуются 3 единицы сырья S2)Определить затраты сырья, необходимые для осуществления следующего выпуска товаров:
'150^ 120 80
Решение. Затраты Sy составляют: 5 • 150 + 0 • 120 + 4-80 ед.,
5 0 4 З 1 4
150 120
80
а затраты S2 составляют: 3_150 + 1 • 120 + 4-80 ед. Отсюда видно, что вектор-столбец S = (s^J7 затрат сырья может быть записан в виде произведения
S = A с =
(1070 [ 890
J
Допустим, что кроме этих данных указаны еще и стоимости каждого вида сырья (в расчете на единицу сырья):
£ = (20 30).
Тогда стоимость всего затраченного сырья будет 201070 + 30 • 890 = 48100 или, в матричной записи:
Стоимость сырья = ( 20 30 ) ^ j =р А с.
Разумеется, если будет необходимо решить другую подобную задачу, то можно, не повторяя рассуждений, сразу записать ответ в виде р А с.
36
in ■
'21 Л1
+ атп хп
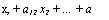 (2.1)
(2.1)
aml*l+flm2x2 +
Ми *2n
Введем в рассмотрение матрицы:
J21
X =
B =
42
hi
А =
Тогда систему (2.1) можно заменить единственным уравнением
АХ=В. (2.2)
Действительно, матрицы АХ и В имеют один и тот же размер т х 1, т. е. каждая из них представляет собой столбец «высоты» т. Приравнивая друг другу первые элементы этих столбцов, получим
а„ Xi+al2x2 + ...+alnxn = blt
что в точности совпадает с первым уравнением системы (2.1). Аналогичный результат дает сравнение вторых элементов, третьих и т. д. В итоге получаем, что уравнение (2.2) равнозначно системе уравнений (2.1).
Уравнение (2.2) называют .матричном записью системы (2.1).
Например, система
| jc, 2х2 + 5х3 = 0 І 2х, + Ъх2 6;с3 = 4
в матричной записи выглядит так:
(■
'1-2 5Ї 2 3-6
*3
Обсуждение Математика в экономике
Комментарии, рецензии и отзывы
