§ 3.5. модель международной торговли.

§ 3.5. модель международной торговли.

Собственные векторы и собственные значения матриц

Модель международной торговли (кратко: модель обмена) служит для ответа на следующий вопрос: какими должны быть соотношения между государственными бюджетами стран, торгующих между собой, чтобы торговля была взаимовыгодной, т. е. не было значительного дефицита торгового баланса для каждой из стран-участниц.

Проблема достаточно важна, так как дефицит в торговле между странами порождает такие явления, как лицензии, квоты, таможенные пошлины и даже торговые войны.

Для простоты изложения рассмотрим три страны-участницы торговли с государственными бюджетами Хх, Х2, Х3, которые условно назовем США, Германия и Кувейт. Будем считать, что весь госбюджет каждой страны тратится на закупки товаров либо внутри страны, либо на импорт из других стран. Пусть, скажем, США тратят половину своего бюджета на закупку товаров внутри страны, 1/4 бюджета — на товары из Германии, оставшуюся 1/4 бюджета — на товары из Кувейта. Германия тратит поровну свой бюджет на закупку товаров в США, внутри страны и у Кувейта. Кувейт, в свою очередь, тратит 1/2 бюджета на закупку товаров у США, 1/2 бюджета на закупки в Германии и ничего не закупает внутри страны.

Введем структурную матрицу торговли:

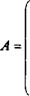
США Германия Кувейт

І І"!

3 2

III

4 3 2

± 1 О

4 3 J

Вообще, пусть ujj — часть госбюджета, которую j-я страна тратит

на закупки товаров i'-й страны. Заметим, что сумма элементов матрицы А в каждом столбце равна единице.

После подведения итогов торговли за год страна под номером і получит выручку р. = ап Хх + аа Х2 + ai3 Х3. Например, США будут иметь выручку

Pl= Х + Х2 + {ХЪдоля США доля Германии доля Кувейта

Для того чтобы торговля была сбалансированной, необходимо потребовать бездефицитность торговли для каждой страны:

р{ £ Х( для всех і. (312)

Пр едложение 1. Условием бездефицитной торговли являются равенства рх = Z„ і = 1, 2, 3.

Доказательство. Предположим, что р( > Х{ для некоторого і, например, для і=1. Запишем условие (3.12) для всех і:

а х+а2Х2 + агхз>х '

а2 Х + а22 Х2 + а23 Х3 ^ Х2 '

азхХх + а32Х2 + а33Х3>Х3. Сложив все эти неравенства, получим:

(а, , + а2Х + а31) Хх + (а12 + д22 + а32) Х2 + (в13 + а23 + а33) Х3 > >ХХ +Х2 + Х3.

Поскольку все суммы в скобках в левой части неравенства равны I, то получим противоречивое неравенство

Хх +Х2 + Х3>ХХ + Х2+Х3.

Следовательно, наше предположение о том, что рх > А",,неверно. Доказательство завершено.

В матричной форме утверждение, содержащееся в предложении 1, выглядит следующим образом:

АХ=Х, (3.13)

где

Х =

(Хх

~(Х1< Хз)

хз ,

называется

Обобщая равенство (3.13), рассмотрим следующее.

Определение 1. Ненулевой вектор х =

собственным вектором квадратной матрицы А порядка л, если

Ах = XI, (3.14)

где X — некоторое число.

При этом число X называется собственным значением матрицы А. Говорят так: х есть собственный вектор матрицы А, принадлежащий ее собственному значению X.

Таким образом, в разбираемом примере из соотношения (3.13) следует, что «вектор бюджетов» X является собственным вектором структурной матрицы торговли А, а соответствующее собственное значение равно 1. Существование такого собственного вектора вытекает из следующей теоремы.

Теорема. Если в матрице А сумма элементов каждого столбца равна 1, то имеется собственный вектор, принадлежащий собственному значению 1.

По условию

Положим, x = (xvx2)T — вектор-столбец. Тогда из соотношения

-1

(3.14) следует, что

= Х

т. е.

X] + 2х2 = ^Х,

—jc, + 4х2 = Хх2

или

(3.15)

' (1-Х)*, + 2х2 = О -хх + (4-Х)х2 = О

Если вектор х — собственный, то это означает, что однородная система уравнений (3.15) имеет ненулевое решение. Согласно последней теореме § 2.9 это условие эквивалентно тому, что определитель системы (3.15) равен нулю:

1-Х 2 -1 4-Х

= 0,

откуда следует, что

аи -1 + д21 + а3, = О,

«12 + «22-1 +«32 = 0> «13 + «23 +«33 _1 =0

или х2-5Х + 6 = 0 =* Л,, = 2, Х2 = 3. Таким образом, собственными

значениями матрицы А будут числа 2 и 3.

Найдем соответствующие собственные векторы. Подставим Х = 2иХ = Зв систему (3.15):

Эти соотношения показывают, что сумма строк матрицы А-Е равна нулевому вектору, т. е. матрица А-Е—вырожденная. Согласно последней теореме § 2.9 система уравнений

(А-Е)х = 0

имеет ненулевое решение х = х0. Это означает, что х0 — собственный вектор матрицы А, отвечающий собственному значению Х= 1.

Пример 1. Найдем собственные векторы и собственные значения следующей матрицы порядка 2:

I 2

ч-1 4

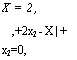Я. = 2,

-2х, + 2х2 = 0

х, =/, х2 = /,

-х, + 2х2 = О -х, + 2х2 = О,

х, = 2/, х2 = Г,

х = /(2, 1), /*0,

х = Г(1, 1), »*0.

Рассуждения из примера 1 можно обобщить на случай произвольной матрицы А порядка п. Условие (3.14) можно переписать в виде:

или

(3.16) 79

Ах Хх = 0, (А-ХЕ)х = 0.

Однородная система уравнений (3.16) тогда и только тогда имеет ненулевое решение , когда ее определитель равен нулю:

И-А£| = 0. (3-17)

Если раскрыть данный определитель, как в рассмотренном примере 1, то получится многочлен степени л относительно X, называемый характеристическим многочленом матрицы А.

Определение 2. Уравнение

А~Щ = 0

называется характеристическим уравнением матрицы А.

Таким образом, собственные значения матрицы А являются корнями ее характеристического уравнения.

Замечание 1. Если вектор х является собственным вектором матрицы А, принадлежащим собственному значению X, то для любого числа к * 0 вектор кх — тоже собственный вектор А, принадлежащий к. Действительно, если х — решение уравнения (3.16), то (А-ХЕ) х = 0. Но тогда (А-ХЕ)(кх) = к(А-ХЕ)х = Аг-0 = 0.

3 амечание 2. Одному собственному значению может соответствовать несколько линейно независимых собственных векторов.

Пример 2. Найти собственные значения и собственные векторы матрицы.

(3 0 0>

3 0

1 3

о о

3-А.

о

3-Х

1

Запишем характеристическое уравнение:

3-Х

= 0,

о I

или (3-Я.) =0. Следовательно, X = 3 — единственное собственное значение матрицы А. Система уравнений (3.16) для отыскания собственных векторов сводится к единственному уравнению:

хх +х2 = 0,

или х, = -х2. 80

Положим,х2 = а, х3 = Ь,и получим общее решение системы (3.16)

х{=-а, х2 = а, х3-Ь,

т. е. собственный вектор х = (-а, а, Ь) представляется в виде линейной комбинации

Зс = а(-1;1;0) + 6(0;0;1) двух линейно независимых векторов ах = (-1; 1; 0) и а2 = (0; 0; 1).

Вернемся к отысканию собственного вектора X в модели международной торговли. Система уравнений для нахождения X имеет вид (3.13), т. е.

'2 3 2

і Л 1 4 3 2

1 -'

Нетрудно найти общее решение этой системы:

Х} = 2Х3 Х2 

поэтому в качестве собственного вектора можно взять вектор

Z=(4;3;2).

В частности, это означает, что сбалансированность торговли этих трех стран может быть достигнута только в том случае, когда госбюджеты находятся в отношении

ХХ:Х2:Х3 = 4:3:2.

Заметим, что структурная матрица торговли А — это матрица с неотрицательными элементами. Мы ищем ее собственный вектор X с положительными компонентами. Вопрос о существовании такого вектора будет обсужден в следующем параграфе.

g—3700