§1.10. свойства функций, непрерывных на отрезке

§1.10. свойства функций, непрерывных на отрезке

Напомним, что согласно данному ранее определению, функция f(x), определенная на отрезке [а,б], называется непрерывной на этом отрезке, если она непрерывна в каждой точке отрезка [а,Ъ].

Функции, непрерывные на отрезке, обладают рядом важных свойств. Ниже даются формулировки и доказательства этих свойств. Еще раз обратим внимание читателя на необходимость безусловного знания свойств непрерывных функций на отрезке.

1*. Теорема о существовании корня

Если функция f{x) непрерывна на отрезке [а,Ь] и на концах отрезка принимает значения разных знаков (т.е. fla) -J{b) < 0), то существует точка с е (а;Ь), такая что Лс) = 0 (рис. 1.13).

Доказательство. Предположим, для определенности, что Да) < О, ДЬ) > 0. Разделим отрезок [а,Ь] пополам точкой су Если /(С() = 0, то доказывать нечего. Если же /(с,)*0, то обозначим через [ах,Ьх] ту из половин отрезка [а,Ь], для которой f(ai) < 0, /(6,) > 0 (в случае /(с,) > 0 это левая половина, при /(с,) < 0 правая). Отрезок [ах,Ьх] также разделим пополам точкой с2. Тогда либо Дс2) = 0, и доказывать нечего, либо f(c2) * 0, и тогда обозначим [а2;Ь2] ту из половин отрезка [ах,Ьх], для которой Да2) < 0, f(b2) > 0. Повторяя это рассуждение, мы либо получим точку сп, f{cn) = 0, либо получим бесконечную последовательность вложенных друг в друга отрезков

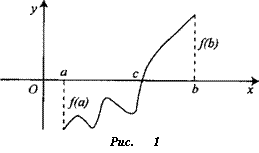[ах;Ьх]=>[а2;Ь2]^...,

причем длины отрезков стремятся к нулю, поскольку каждый следующий отрезок является одной из половин предыдущего отрезка. По теореме о стягивающейся системе существует точка с, принадлежащая всем отрезкам:

ап < с <Ьп,п = 1,2,...

Имеем с jim<3„, а также с = lim Ьп; поскольку функция Дх) непрерывна в точке с, то должно быть

/(c)=lim/(aJ,/(c)=lim/(AJ.

«-♦00 П —► ОО

Но Дап) < 0 для всех и, откуда следует Дс) < 0; аналогично из f(b„) > 0 следует Дс) > 0. Выполнение обоих неравенств Дс) < 0 и/(с) > 0 означает, что Дс) = 0. Свойство 1 доказано. 40

2*. Теорема о промежуточном значении

Пусть fx) непрерывна на[а;й] и /(я)= A,f(b) = В, А * 5. Тогда для любого числа С, расположенного между А и В, найдется такая точка с e(a,b), что /(с) = С .

Иначе говоря, непрерывная функция на отрезке принимает все значения, промежуточные между ее значениями на концах отрезка.

Доказательство. Пусть для определенности А<В. Рассмотрим функциюф(хf(x)-C. Функцияф(х) непрерывна вслед за Дх), причем ф{а) = А С < 0 и ф(Ь) = В С > 0. Согласно свойству 1, найдется точка с є (a; b), для которой <р(с) = 0, т.е. f(c) = C.

3*. Ограниченность непрерывной функции

Функция Дх), непрерывная на отрезке ограничена на этом отрезке.

Иначе говоря, существует такое число А > 0, что |/(*)| ^ Л для всех х из [д; б].

Доказательство проведем от противного. Допустим, что Дх) не ограничена на [a,b]. Положим ах = а,6, = 6 и разделим отрезок [а, ;й, ] пополам. Хотя бы на одной из половин функция Дх) будет не ограничена; зафиксируем одну из таких половин и обозначим ее [а2;Ь2]. Снова разделим отрезок [а2;Ь2] пополам и обозначим [а3;63] ту из половин, где функция не ограничена, и т.д. В итоге получим бесконечную последовательность вложенных друг в друга отрезков:

[ax;bx]=>[a2;b2]z>...,

длины которых стремятся к нулю; при этом на каждом из отрезков функция Дх) не ограничена. По теореме о стягивающейся системе отрезков существует точка х0, принадлежащая всем отрезкам.

Так как fx) не ограничена на [ax;bx], то найдется точка jc, є [а,; Ьх], для которой |/(х,)|>1. Так как Дх) не ограничена на [a2;b2], то найдется точка x2e[a2;b2], для которой |/(х2)| > 2. Продолжая это рассуждение, получим бесконечную последовательность точек хх;х2,..., таких что хп e[a„;b„] и |/(*n)| >n (и = 1,2,...). Очевидно, что lim л,, = дс0. Ввиду непрерывности функции f(x) в точке х0 отсюда должно следовать

lim f(xn) = f(xQ), т.е. последовательность чисел /(х,), f(x2),... должна быть сходящейся. Но в таком случае эта последовательность обязательно ограничена (см. свойство 2 п 2° § 1.2). Между тем неравенства |/(х,)|> 1, |/(х2)|>2 показывают, что эта последовательность не ограничена. Получили противоречие.

4°. Достижение крайних значений

Для всякой функции fix), непрерывной на отрезке [а,й], существует точка с є [а, б], такая что

f(c)> f(x) для всех хе[а;б]

и точка d є[а;б], такая что

f(d)< /(х) для всех х е[а;б].

Иначе говоря, функция, непрерывная на отрезке, достигает на нем как своего наибольшего, так и своего наименьшего значений.

Доказательство. Обозначим E(f) множество значений функции f{x) на отрезке [а; А], т.е.

E(f)={fMxe[a;b]}.

Согласно свойству 3, множество E(f) ограниченное, поэтому оно имеет диаметр (см. § 1.9). Обозначим последний т; М] и докажем, что существует точка с є [я; А], для которой Дс) = Л/, и точка d є[а;б], для которой f(d) = т. Этим, очевидно, и будет доказано требуемое утверждение.

Предположим, что точки с с таким свойством не существует, т.е. что/(х)* М для всех х є[а;б]. Рассмотрим тогда вспомогательную функцию

F(x) =

Знаменатель этой дроби непрерывная на [д; /3] функция (вслед за/(х)),не обращающаяся ни в одной точке в нуль, а потому, ввиду /(х) < М, строго положительная. Согласно свойству 3 не42

прерывных функций, F(x) ограничена на [a;b]. Следовательно, найдется такое число К>0, чтоF(x)< К для всех х e[a;b]. Итак, имеем

<К

M-f(x) или, учитывая, что М /(х) > О,

м-/(*)>!.

Следовательно, /(*) 3x0 означает, что множество £(/)

содержится не только в [m;Af], но и в меньшем отрезке m;M-j^ ( что противоречит выбору отрезка [ти; Af] как диаметра множества £(/) ■

Полученное противоречие доказывает, что точка се[о;б], для которой /(с) = М, существует. Аналогично доказывается существование точки d є [a;b], для которой f(d) = т. Свойство 4 доказано.

5*. Множество значений непрерывной функции

Если функция f(x) непрерывна на отрезке a;b, то множество Ef) значений функции также является отрезком.

Доказательство По свойству 4 существуют точки с и d (отрезка [<з;&]), такие что

/(с)=М = тах/ на [a,ft],

f(d) = т = min/ на [а,6].

Если т = М, то f(x) постоянная функция, и £(/) есть отрезок, состоящий из единственной точки т.

В противном случае (т.е. при т < М) любое число С, заключенное между тиМ, также является (по свойству 2) значением функции, т.е. принадлежит £(/) . Следовательно E(f) есть отрезок [т, Щ. Свойство 5 доказано.

Таким образом, функция, непрерывная на отрезке [а; Ь], отображает его снова на некоторый отрезок.

Следующее свойство функции, непрерывной на отрезке, носит название «равномерной непрерывности». Оно будет использовано в главе 4.

6°. Равномерная непрерывность

Если функция f(x) непрерывна на отрезке [а; Ь], то для любого положительного числа є найдется такое положительное S, что разность значений функции в любых двух точках отрезка, отстоящих друг от друга меньше, чем на 8, по модулю меньше, чем є:

|*.-*2|<<Н/Ы-/Ы<*Доказательство дается в приложении 3 к данной главе.