§ 2.12. цена, предельные издержки и объем производства

§ 2.12. цена, предельные издержки и объем производства

Пусть q выпуск продукции (в натуральных единицах); R(q) -выручка от продаж; C(q) издержки производства, связанные с выпуском q единиц продукции. Тогда прибыль

n(q) = R(q)-C{q).

Предположим, что выполняются следующие условия:

Функции R(q), C(q) определены на полуинтервале [0, +оо) и дифференцируемы при q > 0.

Максимум прибыли достигается в некоторой точке q'* 0.

Замечание. В случае, когда максимум прибыли n{cf) положителен (я"(<7*) > 0), условие q* * 0 естественным образом выполняется, поскольку 7г(0) < 0 (нет выпуска нет выручки, нет выручки нет прибыли).

Пусть условия 1), 2) выполнены. Тогда функция л(д) = R(q) -C(q) дифференцируема и имеет на интервале (0, +оо) максимум в точке q* * 0. По теореме Ферма n'(q>) = 0. Так как nq) = R'(q) -C{q) то в точке q = q* получаем равенство

R'(q') = C'(q-). (2.56)

В экономической теории равенства (2.56) объясняется как правило, согласно которому фирма, максимизирующая свою прибыль, устанавливает объем производства таким образом, чтобы предельная выручка была равна предельным издержкам.

В случае, когда объем производства q не влияет на цену продукции р, имеем R(q) = pq, R"(q) -р. Равенство (2.56) принимает вид

p = C'(q'). (2.57)

Пример 2.32. Найти объем производства, если р = 15, C(q) = q3 + 3q.

Решение Прибыль при производстве q единиц продукции будет n(q) = Sqq33<gr = <y(12 — q2) Очевидно, что n(q) > 0,

если q є[0;\[Ї2]. Так как n{q) непрерывная функция, то на отрезке [0;л/Ї2~] в некоторой точке q' она принимает наибольшее значение на этом отрезке. Поскольку n(q) < 0 при q > Vl2 , то я (у*)наибольшее значение при любом q > 0. Используя равенство (2.57), получим

15 = С'(<Л = 3(**)2+3,

откуда q'= 2. Так как фирма стремится получить максимальную прибыль, то она будет производить 2 единицы продукции.

Фактически мы выяснили, что при цене р = 15 фирма предложит на продажу 2 единицы продукции. Ясно, что немного усложнив рассуждения, мы могли бы найти функцию предложения S(p) данной фирмы (см. § 2.15).

Рассмотрим теперь более общий случай, когда цена продукции р является дифференцируемой функцией р =p{q) от объема выпуска q. Имеем

*Ъ) = {рЩ = P'{q)q + річ) = ~j^1 М + р{ч) = = p(q)(Ehq(q) + ). Равенство (2.56) запишем следующим образом

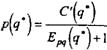
Получим уравнение для цены

(2.58)

Так как EM(q) < 0, то из равенства (2.58) следует, что ценаpiq') не ниже предельных издержек C'(q'). В действительности, если фирма занимает существенную долю рынка, то увеличение ее выпуска приводит к насыщению рынка и падению цены. В этом 110 случае E^iq') < 0 и из (2.58) следует, что цена p(q') больше издержек C'(q').

Предположим теперь, что фирма является монополией. В этом случае при цене р фирма будет производить столько единиц продукции, сколько требуется покупателям при цене р, т.е. q = D(p), где Dip) функция спроса. Таким образом, функция Dip) будет обратной функцией для функции piq). Из свойств эластичности следует, что

E„(q')= E-(P(q')).

Пусть p'=piq') цена, соответствующая выпуску q'. Оптимальный выпуск q' можно представить как q'= Dip') спрос при наилучшей (для монополии) цене р'. Уравнение (2.58) приобретает

вид

р =

ФИ

(2.59)

Пусть, например, ED = -1,2. Тогда^£0'+і| =(~^ + 1j =^>

т.е. цена монополиста р' в 6 раз (!) выше его предельных издержек.

При неэластичном спросе ED < 1 знаменатель дроби в правой части равенства (2.59) £д +1 < 0 и формула (2.59) не имеют смысла. Это значит, что сделанные ранее предположения невыполнимы. Фактически, при неэластичном спросе монополия, стремящаяся увеличить свою прибыль, будет снижать объем выпуска. При этом издержки будут снижаться, а цена и прибыль увеличиваться. В некоторый момент начнется массовый отказ (из-за отсутствия средств) потребителей от продукции данной монополии. Спрос снова станет эластичным.

Пример 2.33. Пусть C(q) = ^q2 издержки фирмы-монополиста, Dip) = 40 2р функция спроса. Найдем зависимость цены р от количества произведенной продукции q. Так как

q = D(p) = 40-2p, то ^q = 20-pnp = 20-^q . Итак, для функции Щр) мы нашли обратную функцию p[q) = 20 — q. Прибыль n(q) имеет вид

^) = (20-i^-iO2 =20q-q

В точке q* максимума прибыли выполняется равенство x'(q') = 20-2q' =0. Находим оптимальный (для монополии) объем производства q' = 10. Соответствующая цена будет

р' = p(q'^ = 20-^q' = 15. При этом предельные издержки

C'(q*^ = 10. Таким образом, цена, наиболее выгодная для монополии, в полтора раза выше ее предельных издержек. Этот же результат можно получить и по формуле (2.59). Действительно,

it I D' "2 Р

Е»М = р^ = р^-Гр = -^Гр>

поэтому E^ip') = £^(15) = -3. Следовательно,

МрНЧ-И"'-1*