§ 4.2. методы интегрирования

§ 4.2. методы интегрирования

1. Интегрирование методом замены переменной

Во многих случаях введение новой переменной позволяет упростить подынтегральное выражение и свести интеграл к линейной комбинации табличных. Такой метод называется методом замены переменной. Он основан на следующей теореме.

Теорема 4.2. Пусть функция х = <p(t) определена и дифференцируема на промежутке Т и Х-множество ее значений, на котором определена функция J(x). Тогда если F(x) первообразная для J[x) на X, то F(<p(t)) первообразная для f(((A )<p ))Ha Т, те на множестве Т выполняется равенство

j/(*H*-«o=Жоно*<4л>

Доказательство. По правилу дифференцирования сложной функции производная левой части равенства

^/)) = /!;W0)^'W=/W0M')'

что совпадает с подынтегральной функцией в правой части равенства, это и доказывает равенство (4.1).

Формула (4.1) называется формулой замены переменной в неопределенном интеграле

г Jx

Пример 4.7. Найти j- dx..

Для того, чтобы избавиться от иррациональности, выполним замену переменной х = /2, t = 4х. Тогда dx = ltdt и наш интеграл примет вид

J 1 + х J 1 + /2 J 1 + '2

= 2^ р/ Jy^r) = 2{t arctg 0 + С.

Возвращаясь к переменной х, окончательно получим J-j^-dx = 2(Vx" arctgVx") + С.

Пример 4.8. Найти ^4-x2dx.

Здесь удобно выполнить тригонометрическую замену х = 2 sin г 0 < х < —. Действительно, подкоренное выражение прини2

мает вид

4-х2 =4-4sin2r = 4(l-sin2r) = 4cos2/, a dx = 2costdt, так что имеем

jyJ4-x2dx = J2 cost ■ 2 costdt = 2 J2 cos2 tdt.

Применяя тригонометрическую формулу «понижения степени»: 2 cos2/ = 1 + cos2/, получим

1^4-х2ах = 2 J(l + cos2t)dt = 2t + sin2/ + С.

Для того, чтобы найти окончательный ответ, выражающий неопределенный интеграл через переменную х, выразим / из фор. х

мулы замены через х: t = arcsin— и заметим, что с dx

J

Воспользуемся табличным интегралом Ш: j — = ln|x| + С. Тогда

-^ = -1пІ2х + 5І + С. 2х + 5 2 1 1

Формулой замены переменной (4.1) пользуются и справа налево. Тогда этот метод называют иногда методом «подведения под дифференциал».

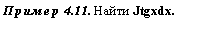V 4 2

Таким образом,

f V 4 — д:2 tic = 2arcsin — + — х-уі4-х2 +С.

J 2 2

Частным случаем теоремы 4.2 является следующая теорема, часто используемая на практике (линейная замена переменной).

Теорема 4.3. Если jf(x)dx = F(x) + C,mo jf(ax + b)dx = -F(ax +b) + C.

Доказательство Положим / = ax + b, тогда dt = adx, откуда dx = -dt, так что f(ax + b)dx = f(t)dt = -F(t) + C, и, вы-ражая x через /, получим то, что требовалось.

Пример 4.9. Найти j"(2x + l)4ax.

Можно, конечно, записать подынтегральную функцию как полином от x, возведя 2х + 1 в четвертую степень, но это будет нерационально, поскольку проще выполнить линейную замену:

\{2x + ydx = ±\{2x + )d{2x + ) =

_ 1 (2х + 1)а |С (2х + 1)3 2 5 10

224

г , rsinx , іч/lcosx і і

Имеем gxdx= dx=-і = -lncosx+C.

J Jcosx J cosx

rd(cosx) ' cosx

Аналогично находится интеграл от ctg х.

2. Метод интегрирования по частям

Метод интегрирования по частям основан на формуле дифференцирования произведения двух функций.

Теор ем а 4.4. Пусть и(х) и v(x) две дифференцируемые функции на промежутке X. Тогда на X выполняется формула интегрирования по частям.

judv -uvjvdu. (4.2)

Доказательство. Имеем формулу для дифференциала произведения функций uv. d(uv) = udv + vdu. Интегрируя обе части равенства, получим слева uv по свойству 2 неопределенного интеграла, а справа сумму интегралов, так что

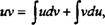
откуда легко получается формула (4.2).

225

Эта формула позволяет свести нахождение неопределенного интеграла judv к неопределенному интегралу jvdu, который может оказаться более простым.

15-1942

Положим и = х, dv = cos xdx. Тогда du = dx, а функция v находится интегрированием v= jcosjrax.TaK что можно положить v = sin х. Подставляя в формулу (4.2), получим

jxcosxdx = х• sinx jsinxdx = xsinx + cosx + С. Пример 4.13. Найти jbxdx.

In xdx =

и = пх, dv = dx _ dx х

dx x

'-, v= jdx = = lnxxix— = xlnxJ x

Удобно все необходимые действия выполнять в одну строку, отделяя вспомогательные записи вертикальными чертами. Итак,

x + C.

Пример 4.14. Найти Jarcsinxrf* Имеем Jarcsin xdx =

xdx

и = arcsin дг, dv = dx dx

du = , v = x

-I

1-х2

Иногда метод интегрирования по частям приходится комбинировать с методом замены переменной, как в случае интегрирования основных элементарных функций у = arcsin х и у = arctg х.

= arcsin x x

4^.

Для получившегося интеграла применим замену переменной

2 1

t = 1 х , dt = -2xdx, откуда xdx = —dt. Поэтому

f ,X = —— = -4~t +C = —Jl-x1 + C. Окончательно имеем jarcsin xdx = x arcsin x + Vl-x2 +C.

Заметим, что поскольку С произвольная постоянная, то получающиеся функции от С можно обозначать по-прежнему С.

Пример 4.15. Найти jx2-e'dx.

f и = х2, dv = e'dx е

Г =du = 2xdx,V= je'dx = e'=x2 <' ~ К =

= x2 ■ e*2 xe*dx =и = Х><Ь = еХ* =x*.e'-2(x.e*je'dx) =

Иногда для вычисления интеграла метод интегрирования по частям приходится применять неоднократно.

u = x2, dv = e'dx du = 2xdx, v = je'dx = e

u = x, dv = e'dx du = dx, v = ex

= x2 e'-2xe' +2e'+C.

В заключение вычислим интеграл

f А /я = J(xJ + l)n'

где и натуральное число. При и = 1 мы имеем табличный интеграл Х(а = 1):

/, = arctg х + С.

Пусть л > 1. Представим 1 в числителе в виде 1 =х2+ 1 дг2, так что интеграл /я представляется в виде разности двух интегралов:

г x2dx 7"-7«-.-J(x2+1)"хЛ

Во втором интеграле применим метод интегрирования по частям

и = х, dv =

(fa = Л, V = J(х2 + і)" 2(л-1)(х2 + 1)Л = (для нахождения v выполните замену t=x2 + l) =

г x2dx J(x" + ir =

15*

227

Подставляя найденный интеграл в формулу для / , получим

" ""' 2(«-іХхЧі)"-' 2(и-1)7- 

т.е. интеграл 1п выражается через интеграл такого же вида с индексом на 1 меньше. Ясно, что за конечное число шагов мы дойдем до интеграла /, и, следовательно, выразим /я в виде некоторой элементарной функции.

Формулы такого вида называются рекуррентными.

Если эта дробь неправильная, т.е. степень многочлена Р(х) не меньше степени многочлена Q(x), то можно выполнить деление с остатком и представить Л(х) в виде суммы некоторого многочлена и правильной дроби.

Пример 4.17. Найти (—г~.

J х 4

xі

Рациональная функция R(x) = —2 неправильная дробь,

х 4

поэтому сначала мы должны выполнить деление с остатком:

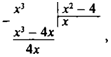Имеем /,=/,+ х _ _ 1 / _ 1 х

т.е. xі = (х2 4) • х + 4х, поэтому подынтегральную функцию

xі 4х

можно представить в виде —; = х + —; . Таким образом,

х -4 х -4

получим