§5.4. степенные ряды 1. степенной ряд. теорема абеля

§5.4. степенные ряды 1. степенной ряд. теорема абеля

Определение. Ряд вида

a0+aix + a2x2+...+anx"+..., (5.42)

где aQ, av av ап, ... некоторая числовая последовательность, называется степенным рядом.

300

Числа av av av ап, ... называются коэффициентами степенного ряда.

Придавая переменной х различные числовые значения, будем получать различные числовые ряды, которые могут сходиться или расходиться. Множество тех значений дс, при которых ряд (5.42) сходится, называется областью сходимости. Область сходимости любого степенного ряда не пуста, поскольку очевидно, что ряд (5.42) сходится для х = 0.

Важную роль при изучении области сходимости степенных рядов играет следующее утверждение.

Теорема 5.11 (теорема Абеля). 1) Если степенной ряд (5.42) сходится при некотором х = xv не равном нулю, то он сходится, и притом абсолютно, при всех х, удовлетворяющих условию х < |jc0|; 2) если ряд (5.42) расходится при некотором х = xv то он расходится при всех х, удовлетворяющих условию х > |jc,|.

Доказательство. 1. По условию числовой ряд

а0+а1х0+а2х02+...+апх0"+...

сходится, поэтому его общий член апх0" стремится к нулю при п -> оо. Следовательно, сходящаяся последовательность {ах0п} ограничена, т.е. существует константа М такая, что |a„x0"| < М для всех п = 0, 1, 2, ... .

(5.43) , приРассмотрим теперь ряд, составленный из абсолютных величин членов ряда (5.42):

чем

|a0| + |a1Jc| + |a2x2|+...+|anxn|+. Пусть |лс|<|лс„|, тогда имеем |anx"| = |a„x£

< 1. Поэтому члены ряда (5.43) не превосходят соответ+...

+ М

М+М

ствующих членов сходящегося ряда

+...+М

суммы бесконечно убывающей геометрической прогрессии. Поэтому ряд (5.43) сходится, а ряд (5.42) сходится абсолютно.

2. Докажем вторую часть теоремы. Предположим противное, т.е. ряд (5.42) расходится при х = xv в то же время для некоторого х, удовлетворяющего условию |jc| >xv ряд (5.42) сходится. По первой части теоремы ряд (5.42) сходится абсолютно при х = xv что противоречит условию. Теорема доказана полностью.

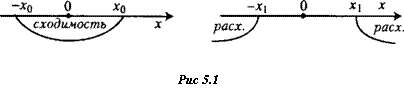Геометрическая интерпретация теоремы Абеля очень проста. Если х0точка сходимости ряда (5.42), то во всех точках интервала (-|*01, |х0|) ряд сходится абсолютно, а если при х = дг, ряд (5.42) расходится, то он расходится и во всех точках, расположенных вне отрезка (-|дс,|, |дс,|) (рис. 5.1).

дится. Тогда по теореме Абеля для всех х таких, что |х|< R, ряд (5.42) сходится, а при всех х, для которых |дс| > R, расходится. Это дает случай 3, что доказывает теорему полностью.

Итак, областью сходимости степенного ряда (5.42) является или единственная точка х = 0, или вся числовая прямая, или интервал (-R, R), к которому могут присоединиться один или оба конца.

Определение. Интервал (-R, R) называется интервалом сходимости ряда (5.42), а число R-радиусом сходимости этого ряда.

Понятие радиуса сходимости будем распространять на все три случая в теореме 5.12: в случае 1 положим R = 0, в случае 2 R = оо.

2. Область сходимости степенного ряда

Теорема Абеля позволяет в принципе описать область сходимости степенного ряда.

Теорема 5.12. Для степенного ряда (5.42) возможны только три случая:

ряд сходится в единственной точке х = 0;

ряд сходится для всех значений х;

существует такое R > 0, что ряд сходится для всех значений х из интервала (-R, R), и расходится для всех значений х вне отрезка [-R, Я].

Доказательство. Обозначим черезXмножество всех положительных значений х, для которых ряд (5.42) сходится.

Если Л" пусто, то ряд сходится только при х = 0. Это дает случай 1.

Пусть X непусто. Если Хне ограничено сверху, то по теореме Абеля ряд (5.42) сходится для всех х. Это дает случай 2.

Останется рассмотреть случай, когда X непусто и ограничено сверху. Существует точная верхняя грань множества X, обозначим ее через Я. Число R обладает тем свойством, что в любой его окрестности имеются точки как принадлежащие, так и не принадлежащие X. Иными словами, в любой окрестности R имеются точки, в которых ряд (5.42) сходится, и точки, в которых он расхо3. Отыскание радиуса сходимости

степенного ряда

от 

Радиус сходимости степенного ряда чаще всего находят с помощью признака Даламбера.

Теорема 5.13. Если существует предел Dlim

(5.44)

личный от нуля, то радиус сходимости степенного ряда а0 + ахх + а2х2 +...+апх" +... равен:

R = — = lim

Доказательство. Рассмотрим ряд, составленный из модулей членов степенного ряда (5.42). По условию существует предел D= lim не равный нулю. Обозначим его через — • По

т.е. при |х|< R.

lim

л->оо

По теореме о сходимости знакопеременных рядов ряд (5 42) сходится при этих значениях х. При х\> R имеем

х

а„х

= и>1,

R

поэтому ряд (5.42) расходится, так как общий член ряда <зпУ не стремится к нулю.

Таким образом, данный ряд сходится внутри интервала (-R, R) и расходится вне отрезка [-R, R], т.е. R радиус сходимости ряда (5.42), и формула (5.44) доказана.

х + Пример 5.18. Найти область сходимости ряда

xJ х"

—+...+—+....

R= lim

П-*со

В данном случае ап = ~,ал+1 = -!_ поэтому

= lim-^-= lim (1 + -1 = l

Следовательно, по теореме 5.13 данный ряд сходится на интервале (-1, 1). Исследуем поведение ряда на концах интервала, т.е. при х = ± 1. При х = 1 получаем гармонический ряд, следовательно, ряд расходится. При х = -1 получаем знакочередующийся ряд

. 1 I (-О" „ гТаким образом,'областью сходимости данного степенного ряда является полуинтервал [-1,1). Позже мы увидим, чт™этоТРряд в области сходимости равен функции -1п(1 ~х

-1 + — — +...+ +..., который сходится по признаку Лейбница.

2 3 п _

Пр им ер 5.19. Найти область сходимости степенного ряда

х2 Xі г" 1 + Х + —+ —+...+ —+ 2! З! „ "

а„ =■

всех"™^^™ "1 («эн-Фает°Риал») обозначает произведение всех натуральных чисел до п включительно. В данном случае

1

ап+1 =

304

поэтому R = lim—:—; г= Нт(я + 1) = оо. Следовательно, данный степенной ряд сходится абсолютно на всей числовой прямой. Опять-таки, для каждого х сумма данного ряда дает значение функции^*.

Пример 5.20. Найти область сходимости степенного ряда

х + (2х)2 + (Зх)3+...+(лх)п+.... Общий член ряда равен (их)", поэтому каково бы ни было значение х * О, при и > Л имеем (л | х |)" > 1, т.е. ряд расходится.

И

Область сходимости данного степенного ряда состоит из одной точки х = 0, радиус сходимости R = 0.

4. Свойства степенных рядов

Пусть функция Дх) является суммой степенного ряда

fix) = a0+aix+a2x2+...+axn+..., (5.45) интервал сходимости которого (-R, R).

В этом случае говорят, что функция Дх) на интервале (-R, R) разлагается в степенной ряд.

Вьшолняются следующие теоремы о свойствах степенных рядов, которые мы приведем без доказательства.

Теорема 5.14 (о почленном дифференцировании степенного ряда). Пусть функция Дх) разлагается на интервале (-R, R) в степенной ряд (5.45). Рассмотрим степенной ряд

а, + 2а2х+...+ пах"-1+..., (5.46)

полученный почленным дифференцированием ряда (5.45). Тогда:

ряд (5.46) имеет тот же радиус сходимости R, что и ряд (5.45);

на всем интервале (-R, R) функция Дх) имеет производную f '(х), которая разлагается в степенной ряд (5.46).

Применяя теорему 5.14 повторно, заключаем, что вторая производная / '{х) также существует и равна сумме ряда, полученного двукратным почленным дифференцированием ряда (5.45). Ана20-1MJ 305

логичное заключение справедливо и для третьей производной и т.д. В итоге получаем следствие.

Следствие. Функция fix), которая разлагается в степенной ряд (5.45) на интервале (-R, R), бесконечно дифференцируема на этом интервале. Разложение в степенной ряд для любой производной получается почленным дифференцированием ряда (5.45). При этом радиусы сходимости соответствующих рядов равны радиусу сходимости ряда (5.45).

Теорема 5.15 (о почленном интегрировании степенного ряда). Если функция fix) разлагается в степенной ряд на интервале (-R, R), то она интегрируема в этом интервале. Интеграл от суммы ряда равен сумме интегралов от членов ряда.

Иными словами, если [х,, x2]cz(-R, R), то

^f(x)dx = J(d0 + ахх + а2хг+...+а„х" + ...)dx =

х х

х2 х2 х2 х2

= ja0dx+ jaxxdx + ja2x2dx+...+ jaflx"dx+...

jr| Х| *! і]

Особый интерес представляет интегрирование степенного ряда (5.45) с переменным верхним пределом по интервалу [0, х ], где

y(x)dx = a0x + -^ + ^-+...+-*—-+.... (5.47)

В этом случае получаем степенной ряд (5.47), который имеет тот же радиус сходимости, что и ряд (5.45).