9.17. метод отсечений для целочисленных задач линейного программирования
9.17. метод отсечений для целочисленных задач линейного программирования
Дана полностью целочисленная задача линейного программирования:
/ = Хунтах), (9.47)
j=i
Jdai]xj=bi, і = 1,2,..., т, (9.48)
Xj>0, j=,2,...,n, (9.49)
Xj — целое, j=,2,...,n. (9.50)
Метод отсечений опирается на следующее утверждение: если ослабление задачи (9.47)—(9.50) имеет нецелочисленное оптимальное опорное решение а0, то существует неравенство вида
&jXj>A, (9.51)
У=1
которому а0 не удовлетворяет, а любое допустимое решение исходной целочисленной задачи — удовлетворяет.
Неравенство (9.51), обладающее указанными свойствами, называют правильным отсечением. Правильное отсечение, например, можно построить следующим образом.
Симплекс-таблицу для ослабления задачи (9.47)—(9.50) приведем к базису а0, все оценки которого не положительны. В полученной таблице выбираем строку с дробным свободным членом dp:
256
| *1 | Хп | ||||
| §1 | К | 8„ |
 |
Так как [1/2] = 0, [-5/2] = -З, [1] = 1, [0] = 0, [3/2] = 1, то по первой строке можно построить правильное отсечение (l/2)Xj + + (1/2)х2 > 1/2. Аналогично по второй строке строится правильное отсечение (l/2)Xj + (2/3)х2 > 1/3. •
В дальнейшем будем считать, что коэффициент при неизвестных и свободные члены системы линейных уравнений (9.48) являются целыми числами.
Для решения целочисленной задачи (9.47)—(9.50) методом отсечений необходимо выполнить ряд последовательных шагов. На каждом шаге решается задача линейного программирования; если эта задача оказывается неразрешимой, то и исходная целочисленная задача неразрешима.
Первый шаг. Находят оптимальное опорное решение Рх = = (х[^ х^ х^) ослабления целочисленной задачи (9.47)—(9.50). Если Pj окажется целочисленным, то оно — искомое. В противном случае строят правильное отсечение, записывают его в виде
^.-хп+1=А®, xn+l>0, и добавляют к системе ограничений исходной задачи.
257
к-й шаг (к > 2). Находят оптимальное опорное решение
$к ~ (ХР> х2®> xnfc)'хл+1' ^п+к-і) ослабления задачи, построенной на предыдущем шаге. Если pfe целочисленно, то ак = (xf
х^) — оптимальное решение исходной задачи (9.47)—(9.50). В противном случае строят правильное отсечение
п+к-1
X -kfx;-xn+k=A« хп+к>0,
и добавляют его к системе ограничений исходной задачи, полученной на (к 1)-м шаге. После этого выполняют (к+ 1)-й шаг.
При определенных условиях всегда можно гарантировать конечность этого алгоритма, т.е. через конечное число шагов либо будет найдено оптимальное решение, либо будет установлено, что задача неразрешима.
9.18. Метод ветвей и границ
для целочисленных задач линейного программирования
Дана оптимизационная задача минимизации (V, /, Q). Предположим, что допустимое множество Q разбито на конечное число непересекающихся подмножеств:
Q = А и А2 и... и Ак и... и 4. (9.52)
Выберем некоторое подмножество Ак и тоже разобьем его на конечное число непересекающихся подмножеств:
А=і^и...иіЄ>. Тогда Q можно представить в виде
Q = 4 и... и А-1 и вік) и u ^ Л+1 ^ ^ 4(9-53)
Переход от разбиения (9.52) множества Q к разбиению (9.53) того же множества называют ветвлением с помощью подмножества 4.. Схематически процесс ветвления можно изобразить так:
Q
л
4—4t—Л
/
о(к) о(к)
258
Если А — некоторое подмножество множества Q, то оценкой подмножества А называется число Е,(А) такое, что f(x) > Ъ,{А) для любого х є А.
Для решения задачи минимизации (V, /, Q) методом ветвей и границ выполняют ряд последовательных шагов.
Нулевой шаг. Допустимое множество Q некоторым способом разбивают на конечное число непересекающихся подмножеств.
Первый шаг. Вычисляют оценки образовавшихся подмножеств и выбирают подмножество с наименьшей оценкой. Если в выбранном подмножестве удается найти элемент а0 такой, что /(а0) совпадает с оценкой этого подмножества, то а0 — оптимальное решение задачи (К, /, Q). В противном случае осуществляют ветвление с помощью выбранного подмножества и переходят ко второму шагу.
А>й шаг (к > 2). Рассматривают разбиение множества Q на подмножества, которое было получено на предыдущем шаге. Для каждого из этих подмножеств находят его оценку и выбирают подмножество с наименьшей оценкой. Если в выбранном подмножестве удается найти элемент а0 такой, что /(а0) совпадает с оценкой этого подмножества, то а0 — оптимальное решение задачи (V, /, Q). В противном случае осуществляют ветвление с помощью выбранного подмножества и переходят к следующему шагу.
Для применения метода ветвей и границ в каждом конкретном случае необходимо:
задать первоначальное разбиение допустимого множества на конечное число непересекающихся подмножеств;
определить способ разбиения подмножеств, с помощью которых на каждом шаге осуществляются ветвления;
сформулировать правило вычисления оценок всех встречающихся подмножеств.
В основном метод ветвей и границ применяют для решения целочисленных задач линейного программирования, так как именно в этом случае часто удается найти приемлемое правило вычисления оценок. При этом оценки находят либо с помощью решения некоторых вспомогательных задач линейного программирования, либо на основе комбинаторной структуры исходной задачи.
Рассмотрим задачу о коммивояжере с матрицей расстояний С = (с~) порядка и. Обозначим через Q множество всех маршрутов, при которых коммивояжер, выезжая из города Av побывает во всех
259
остальных городах по одному разу и вернется в Av Пусть Qt i2j3,...jk, 2 < к < п 1, — подмножество множества Q, состоящее из всех маршрутов, при которых коммивояжер, выезжая и.зАр последовательно посещает города Aii, Ai .
Множество Q можно разбить на непересекающиеся подмножества Qj 2, Qx 3, Qj п. Для осуществления ветвления с помощью подмножества Qx іг ^ 'ік, 2 < к < п 2, это подмножество разбиваем на подмножества вида ПМг;з/ь у, где у* 1, /2, *'3, ik.
Например, подмножество Qt 2 разбиваем на подмножества
Q
1,2, п'
^1,2,3' ^1,2,1
Множество £/2;/3,...,ік ПРИ к = п — 1 состоит из единственного маршрута, и с помощью него ветвление не выполняется.
Оценку подмножества Ц,^,...,^,^ 2 < к < п 1, находим по формуле
)
.+ с,
'к-1'к
+ mm
j*l,i2,-,>k
к) min са
ІФІ,І2>-''к
l*h к
Если к = п 1, то оценка подмножества Ц,^^...^ совпадает с длиной единственного маршрута, входящего в это множество.
9
9 *
3 1
О Пример. Если
ю
і
С =
11 4 11
Ґ * 2 11 5 1
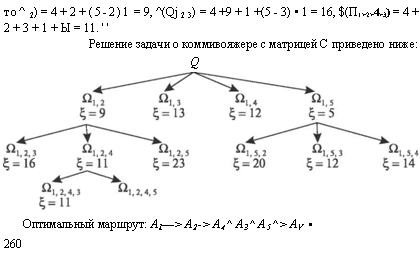
9.19. Метод Беллмана для решения целочисленных задач линейного программирования
Дана целочисленная задача линейного программирования
/ = Хунтах), (9-54)
2,gjXj * Ъ, (9.55)
0<Xj<dj, Xj — целое, j= 1,2,и, (9.56)
где gj, d. (j 1, 2,и), b — целые положительные числа.
Обозначим через z 0, 1, 2, b, множество всех целочисленных решений системы неравенств
л 7=1
О <*,<</., у=1,2,...,и,
Множество Q? состоит из одного нулевого вектора при z 0 и совпадает с множеством допустимых решений задачи (9.54)—(9.56) при z Ь. Кроме того, если а = (xv хк, хп) є Qz, то 0<xk<mm(dk,z/gk).
Пусть (yk(z), к 1, 2, и, — наибольшее значение функции
к
X на множестве Q?. Функции ф^г), ф2(г),Ф„(г), определенныеприг = 0,1, 2,называются функциями Беллмана для задачи (9.54)—(9.56). Для этих функций имеют место следующие равенства:
\%(z) = n max {у^}, (9.57)
ху целое
Ф*(*) = max (ул+ф^и-сГЛ)}. (9.58)
0<xfc<min(^,z/gfc) Xj. целое
Обозначим через x°ji(z), к = 1,2, п, то целое значение хк, 0<хк< min (rfL, г/сГо)) при котором достигается максимум выражения, стоящего в правой части соответствующего равенства.
261
Задачу (9.54)—(9.56) решают по следующей схеме:
По формуле (9.57) находят все значения функции ф^г), z = 0,1, 2,Ь. Одновременно определяют х*(г).
Используя рекуррентное соотношение (9.58), последовательно находят функции Беллмана <p2(z), ф„_і(г) и значение функции ф (г) при z = Ъ. Одновременно определяют х^(г), ...jX*^) и х*п(Ь).
Строят оптимальное решение а0 = (xj, х2,хи1, х°п) задачи (9.54)-(9.56), полагая х° = х*(й), = х*_,(Ь g„x°), х? = = xX(b-g/n-gn_/n_l-...-g1xl).
О Пример. Решить следующую целочисленную задачу: /= 3Xj + 4х2 + 5х3(тах), 2Xj + 5х2 + 4х3 < 12, 0<ху.<3, 7=1,2,3.
В данном случае ф, (z) = max {Зх,}. Значения этой функции
О^х^тіпО.г/г)
и соответствующие числа x*(z), z = 0, 1, 2, 12, приведены в табл. 9.8.
Таблица 9.8
| Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Фі(г) | 0 | 0 | 3 | 3 | 6 | 6 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| x(z) | 0 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
По определению, ф2(г) = max {4х2 + \%(z 5х2)}.
0<х2^пші(3,г/5)
 В табл. 9.9 приведены числа 4х2 + фх(г 5х2) при z = 0, 1, 2,12 и 0 <х2 < min (3, z/5), все значения функции ф2(г) и числах*(г).
В табл. 9.9 приведены числа 4х2 + фх(г 5х2) при z = 0, 1, 2,12 и 0 <х2 < min (3, z/5), все значения функции ф2(г) и числах*(г).
Так как min(3, 12/4) = 3, то <р3(12) = rnax^{5x3 + ф2(12 4х3)}, т.е.
ф3(12) = max{0 + 13, 5 + 9, 10 + 6, 15 + 0} = 16. При этом х*(12) = 2. Тогда
х° = х*(12) = 2; х° = х*(12 2 • 4) = х*(4) = 0;
х° = х*(12 2 ■ 4 0 • 5) = х*(4) = 2.
Следовательно, а0 = (2; 0; 2) является оптимальным решением нашей задачи, причем/(а0) ф3(12) 16. •
9.20. Задачи нелинейного программирования
Оптимизационная задача (К, /, Q) называется задачей нелинейного программирования, если целевая функция/является функцией л переменных (F= R"), а допустимое множество Q — множеством решений некоторой системы уравнений и неравенств с л неизвестными.
Так как любое уравнение равносильно системе двух неравенств
Шх1,х2,...,хп)<0,
-Ф(х1,х2,...,хп)<0,
то можно считать, что допустимое множество Q задачи нелинейного программирования задается только неравенствами.
Таким образом, задача нелинейного программирования — это задача максимизации или минимизации целевой функции
/=/(х1,х2,...,хя) (9.59)
на множестве решений системы неравенств, которую удобно записывать в следующем виде:
ГФДдсі,дс2,...,дсв)^0, і = ,2,...,т, (9.60) [xj >0, jeJczN = {l,2,...,n}, (9.61)
где Ф/Xj, х2, хи) — некоторые функции, определенные на всем пространстве R".
Задачи нелинейного программирования образуют широкий класс оптимизационных задач. В частности, к этому классу принадлежит задача максимизации или минимизации функции л переменных на всем пространстве R".
263
Кроме того, класс задач нелинейного программирования включает в себя задачи линейного программирования.
Введем следующие обозначения:
(R")+ = {M(xv х2,хп) є R" | Xj > 0J= 1, 2,и},
Щ = {M(xv x2,..., xn) є R" I x. > 0,j є /},
гдє/с:уУ= {1, 2,и}. Очевидно, что:
eani/=0,ToR}=R";
eaiH/=7V,ToR}=(R")+.
Функция
т
ЦМ,Р) = ДМ)-^уіФі(М)
(где M(xv х2,хп) є R", P(yv у2,yj є (Rm)+) называется функцией Лагранжа для задачи максимизации (9.59)—(9.61). Для задачи минимизации функция Лагранжа имеет вид
т
ЦМ,Р) = -ДМ)-^уіФі(М).
i=l
Точка MQ(x[°,Xj,х®) є R" является точкой Куна — Тиккера для задачи (9.59)—(9.61), если существует точка Р0(ух, у®, у^) є (Rm)+ такая, что справедливы условия Куна — Таккера:
|^(ilf0,P0)<0, j є/, |^(ilf0,P0)>0,
dXj дуі
—Ш0,Р0) = 0, jeNJ, y°?-(M0,P0) = 0, i = l,2,...,m,
dXj дУі
x°^-(M0,P0) = 0, j<=J.
О Пример. Найти точки Куна — Таккера для задачи
f=x1x2(max), (9.62)
т+т-1> (9-63)
х2 > 0. (9.64)
264
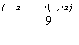 Функция Лагранжа в данном случае имеет вид Цх1,х2,у1) = х1х2-у1' "
Функция Лагранжа в данном случае имеет вид Цх1,х2,у1) = х1х2-у1' "
J
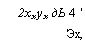 |
дхх
= х,
2х2ух дЬ
(Л
9
то для отыскания точек Куна — Таккера имеем систему
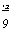
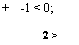
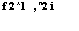
<0,
х2 4 и,
2х2уу
■^2
4 ~9
4
Уі
х2>0, ^>0
= 0;
Решив ее, найдем точки М^х^ 0), где -2 < хх < 0, и М2(уі2; з/у/2), которые являются искомыми точками Куна — Таккера. •
Необходимое условие оптимальности для задачи нелинейного программирования можно сформулировать следующим образом. Пусть М0 — оптимальное решение задачи (9.59)—(9.61), причем функции ДМ), Ф((М), і = 1, 2, т, дифференцируемы в этой точке. Если MQ — неособая точка допустимого множества задачи (9.59)—(9.61), то она является точкой Куна — Таккера этой задачи.
Таким образом, если допустимое множество Q задачи (9.59)-(9.61) не имеет особых точек, а функции ДМ), Ф,(М), і = 1,2,т, дифференцируемы во всех точках Q, то оптимальное решение этой задачи следует искать среди точек Куна — Таккера.
О Пример. Оптимальное решение задачи (9.62)—(9.64) находится среди точек Куна — Таккера этой задачи: Мх(хх 0), где -2 < Xj < 0, и М2(у/2; 3/V2). Так как /(МЛ = 0, a ДМ2) = 3, то М2(лІ2; з/л/2) — оптимальное решение задачи (9.62)—(9.64). •
Следует отметить, что необходимое условие оптимальности малопригодно для решения большинства задач нелинейного программирования, так как лишь в редких случаях удается найти все точки Куна — Таккера задачи нелинейного программирования.
265
Пара точек М0 є R", Р0 є (Rm)+ называется седловой точкой функции Лагранжа, если
ЦМ,Р0)<ЦМ0,Р0)<ЦМ0,Р)
для всех Me Щи Ре (Rm)+.
Достаточное условие оптимальности для задачи нелинейного программирования: если (М0, Р0) — седловая точка функции Лагранжа для задачи (9.59)—(9.61), то М0 является оптимальным решением этой задачи.
Это условие в общем случае не является необходимым: функция Лагранжа может не иметь седловых точек, в то время как исходная задача нелинейного программирования обладает оптимальным решением.
При решении задач нелинейного программирования в общем случае сталкиваются с большими трудностями. Точные методы решения найдены лишь для специальных классов задач нелинейного программирования, в основном когда система ограничений состоит только из линейных неравенств. Известны различные методы, позволяющие найти оптимальное решение приближенно. Однако эти методы дают достаточно хорошее приближение лишь для задач выпуклого программирования.
Обсуждение Справочник по математике для экономистов
Комментарии, рецензии и отзывы
