11.9. матрицы графов
11.9. матрицы графов
Граф может быть задан разными способами: рисунком, перечнем вершин и ребер (или дуг) и пр. Один из самых удобных способов — задание графа с помощью матрицы.
Пусть некоторый граф G имеет п вершинpv р2,рп и т ребер ар а2,ат. Построим матрицу, имеющую п строк и т столбцов. Каждая строка матрицы будет соответствовать вершине графа, а столбец — ребру. В столбце а. все элементы, кроме двух, будут равны нулю.
Для неориентированного графа в строках матрицы, соответствующих концевым вершинам ребра а., ставят 1, а в остальных строках — 0.
Для ориентированного графа в строке, соответствующей начальной вершине дуги ос., ставят число +1, а в строке, соответствующей конечной вершине, — число -1.
316
Для графов, изображенных на рис. 11.9 и 11.12, матрицы имеют соответственно следующий вид:
| «і | ot2 | «3 | «4 | «5 | «6 | «i | oc2 | oc3 | «4 | «5 | |||
| Pi | 1 | 1 | 0 | 0 | 0 | 0 | Pi | 1 | 0 | -1 | 1 | 0 | |
| Pi | 0 | 1 | 1 | 0 | 1 | 1 | Pi | -1 | 1 | 0 | 0 | 0 | |
| Pi | 0 | 0 | 0 | 0 | 0 | 1 | Ръ | 0 | -1 | 1 | -1 | 1 | |
| Pa | 0 | 0 | 0 | 1 | 1 | 0 | Pa | 0 | 0 | 0 | 0 | -1 | |
| Ръ | 1 | 0 | 1 | 1 | 0 | 0 | |||||||
Построенные матрицы называются матрицами инциденций графа.
Матричное представление графа является наиболее удобной формой задания графа при вычислениях на компьютере.
11.10. Максимальные потоки в сети
Поток на графе — это совокупность однородных объектов, пересылаемых из одной вершины в другую по его дугам. Если вершины р и q соединены дугой а = (р, q), то поток из/? в я обозначается fip, q). Таким образом, поток — это некоторая функция, заданная на дугах графа.
Пусть имеется ориентированный граф, на дугах которого определена функция С(р, q). В потоковых задачах С(р, q) обычно означает пропускную способность дуги (р, q) или стоимость перевозки единицы потока по этой дуге.
Дивергенцией потока f в вершине р называется разность выходящих и входящих потоков:
tivf(p)= X f(P>9)~ X f(r,P), (П-5)
(p,q)eA(p) (г,р)єВ(р)
где А(р) — множество дуг, выходящих из вершины р, а В(р) — множество входящих в нее дуг.
Вершины, в которых dif(p) > 0, называют источниками потока /, а вершины, в которых dif(p) < 0, — его стоками.
Сложим дивергенцию потока / во всех вершинах графа. Очевидно, что
D = ^diwf(p) = 0. (11.6) р
317
Пусть задана сеть, в которой выделены две вершины: ли/. Рассмотрим такие потоки /(а), что:
1) 0 < /(а) < С(а) на всех дугах а;
2) drvjip) 0 при всехр, кроме, быть может, р = s ир = t.
Вершины s и t называются полюсами сети, а остальные вершины — внутренними.
Из (11.4) следует, что diwf(s) -divy(0 М. Если МО, то поток называется циркуляцией. В противном случае (М Ф 0) вершина s является источником потока, а вершина t — стоком. Число М > 0 называется мощностью потока /
Задача состоит в том, чтобы найти поток /максимальной мощности, удовлетворяющий условиям 1 и 2.
Если заданная сеть G содержит параллельные дуги, нужно рассмотреть новую сеть G', у которой будут те же вершины, что и у G, но параллельные дуги аир склеены. При этом пропускная способность склеенной дуги у есть С(у) = С(сх) + С(Р). После получения решения / для сети G' оно разбивается на сумму /(у) = fy+f2, где 0£/і£С(а),0£/2£С(Р).
Увеличивающая цепь. Пусть заданы сеть Си какой-то поток/на этой сети. Дуги а, в которых /(а) < С(сс), называются увеличивающими, так как поток через эти дуги можно увеличить на величину Д/(ос) = С(ос) /(ос). Множество увеличивающих дуг обозначают А+.
Дуги а, в которых /(а) > 0, называются уменьшающими, так как поток через эти дуги можно уменьшить на величину /(ос). Множество уменьшающих дуг обозначают А~.
Заметим, что дуга ос может принадлежать одновременно множествами и А~.
О Пример. Рассмотрим сеть, изображенную на рис. 11.13, и некоторый поток/. Пусть C(s,p) = 9, С(р, г) = 4, С(и, t) = 4. Возьмем цепь (s,p, г, т, п, t), соединяющую вершины s и t. Вдоль этой цепи можно увеличить поток на минимальную из величин
ДЖ/>) = 9-7 = 2, Д/(р,г) = 4-2 = 2,
f(m,r) = , f(n,m) = 1, Д/(«, 0 = 4-3 = 1.
Очевидно, что мощность потока возрастет на единицу (рис. 11.14). •
318
Рис. 11.13
Рис. 11.14
Рис. 11.15
В общем случае вдоль некоторой цепи, соединяющей вершины S и t, можно увеличить поток, если ее прямые дуги — увеличивающие, а все обратные — уменьшающие.
Максимальный дополнительный поток 8, который можно переслать вдоль такой цепи, равен минимуму из всех Л/(ос) для прямых дуг а и всех /(а) для обратных дуг а.
Алгоритм нахождения увеличивающей цепи:
Находят множество дуг А+ и А~.
Отмечают вершину s (источник).
Далее отмечают некоторые дуги и вершины сети G: если вершина р отмечена, а вершина q не отмечена и дуга а = (р, q) є А+ либо а (q, р) є А~, то отмечают дугу а и вершину q.
В результате получают некоторое подмножество отмеченных вершин, соединенных отмеченными дугами. При этом, отмечая вершину q, нужно одновременно запомнить вершину р, отмеченную ранее, из которой в q привела отмеченная дуга а (прямая или обратная).
Замечание. Приведенный алгоритм не указывает, в каком порядке нужно просматривать дуги. Например, можно сначала просмотреть все дуги, инцидентные s, отметить некоторые вершины в соответствии с правилами; затем просмотреть все дуги, инцидентные отмеченным вершинам, и т.д. В другом варианте всякий раз просматривают дуги, инцидентные последней отмеченной вершине, и т.д. Этот алгоритм позволяет получить увеличивающую цепь из S в t.
О Пример. Применим алгоритм построения увеличивающей цепи к графу, изображенному на рис. 11.15.
Для любой отмеченной вершины будем просматривать все инцидентные ей дуги. Отмечаем источник s. Дуги (s,p), (s, и) отмечаем как выходящие увеличивающие, а дугу (г, s) — как входящую уменьшающую (рис. 11.16).
319
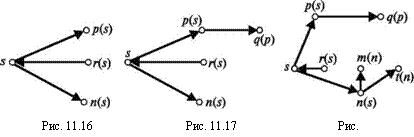 В скобках указаны вершины, соединенные с новыми вершинами отмеченными дугами. Далее просматриваем дуги, инцидентные р (рис. 11.17). Дугу {р, г) не рассматриваем, поскольку вершина гуже отмечена. Далее, просматривая дуги, инцидентные п, отмечаем дугу (и, f), вершину іи дугу (и, /я), вершину т (рис. 11.18).
В скобках указаны вершины, соединенные с новыми вершинами отмеченными дугами. Далее просматриваем дуги, инцидентные р (рис. 11.17). Дугу {р, г) не рассматриваем, поскольку вершина гуже отмечена. Далее, просматривая дуги, инцидентные п, отмечаем дугу (и, f), вершину іи дугу (и, /я), вершину т (рис. 11.18).
На этом просмотр заканчиваем, так как отмечен сток t. Идя в обратном направлении, получаем увеличивающую цепь (s, и, t). •
Алгоритм отыскания максимального потока в сети. Данный алгоритм, использующий увеличивающие цепи, называется алгоритмом Форда. Он состоит из следующих шагов:
Выбирают некоторый поток /(ос) из s в t (например,
До0 = 0).
Находят классы увеличивающих (А+) и уменьшающих (А ) дуг.
Применяют алгоритм поиска увеличивающей цепи из s в t. Если такой цепи нет, то поток / — максимальный. Если цепь С найдена, то переходят к шагу 4.
Находят тіл (Д/(ос)), min /(а).
аєА*пС аєА rC
Пусть 8 > 0 — наименьшее из этих чисел.
Увеличивают поток вдоль цепи С на 8 и переходят к шагу 2.
Очевидно, что построенный таким образом поток удовлетворяет следующим условиям:
До0<С(ос),
div^(p) = 0 при рфь,рфі.
Этот поток является максимальным. Если начальные данные целочисленны, то выполнение алгоритма Форда завершается за конечное число шагов.
320
Обсуждение Справочник по математике для экономистов
Комментарии, рецензии и отзывы
