4.18. асимптоты графика функции одной переменной

4.18. асимптоты графика функции одной переменной

Пусть функция у = /(х) определена при всех х > х0 (х < х0). Если существуют числа к и Ъ такие, что функция fix) -kx-b бесконечно малая при х —> +°° (х -> -°°), то прямую линию у = Ах + Ъ называют асимптотой графика функции у /(х) при х —> +°° (х —» -°°).

При этом если А; Ф О, то асимптоту называют наклонной, если же & = 0 (тогда у Ъ), то горизонтальной.

Условие fix) -kx-b бесконечно малая означает, что

lim [f(x)-kx-b] = О

*->+~

(х-»^о)

и, следовательно, функция Дх) при х —> +°° (х -> -°°) неограниченно приближается к прямой y = kx + b («ведет себя почти как линейная функция»).

125

Если существуют пределы

lim kx и lim [fix) к]Х] = by,

то прямая у к,х + Ь, является правой наклонной (при к, О — горизонтальной) асимптотой графика функции

У =/(*).

Если существуют пределы

fix)

lim = к2 и lim [fix) к2х] b2,

то прямая у = к2х + Ь2 является левой наклонной (при к2 = 0 — горизонтальной) асимптотой графика функции У =/(*)•

Пусть функция у = fix) определена в некоторой окрестности точки х = х0. Если

lim fix) = оо или lim /(х) оо,

X-¥Xq-0 X->Xq+0

то прямая х = х0 является вертикальной асимптотой графика функции y=fix).

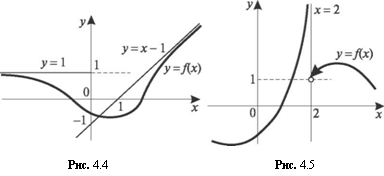
Например, на рис. 4.5 изображен график функции у=fix), имеющий вертикальную асимптоту х = 2, так как lim /(х) = -н». Прех-»2-0

дел справа lim f(x) = l.

х-»2+0

126

4.19. Понятие непрерывности функции в точке

Пусть функция f(M) = f(xv х2,хп) определена на множестве Fc R" и пусть точка М0(х®, х2,х®) є Кявляется его предельной точкой.

Функция f(M) называется непрерывной в точке М0, если для любого числа є > 0 можно указать окрестность Sr(M0) точки М0 так, что для всех точек М є S (М0) n V выполняется неравенство ДМ)-ЛМ0)\<е.

Непрерывность функции ДМ) в точке М0 означает существование предела lim /(М)и равенство этого предела значению функции

M->Mq

в точке Mf., т.е. lim f(M) = f(M0).

М->М0

В этом же случае для любой последовательности точек {Мк}, Мк є V, сходящейся к точке М0, последовательность значений функции f(Mx),f(M2), ...,f(Mk),... сходится кДМ0) (см. п. 4.10).

Условие lim f(M) = f(M0) равносильно следующему услоAf-»M0

вию: lim [f(M) f(M0)] 0. Если при этом точка Мимеет коор-динаты (xv х2,хп), то разностихх х, х2 х2,хп -х® обозначают соответственно через Axv Ах2, Ахп и называют приращениями аргументов, а разность f{M) f(M0) — через Af(M0) и называют приращением функции в точке М0, соответствующим данным приращениям аргументов Axv Ах2, Ахп. Тогда условие lim [f(M) f(M0)] = 0 может быть записано в виде АДМЛ —> 0

при AXj -> 0, Ах2 -> 0,Ахп -> 0 и, следовательно, непрерывность функции f(M) в точке М0 означает, что приращение функции стремится к нулю, когда приращения всех ее аргументов также стремятся к нулю.

В частности, функция у = f(x) одной переменной, определенная в некоторой окрестности точки х0, является непрерывной в этой точке, если для любого числа е > 0 можно указать зависящее от є число 8 > 0 такое, что для всех х, удовлетворяющих условию х х0 < 5, выполняется неравенство |/(х) /(х0)| < є, т.е. lim fix) = /(х0) или lim Af(x0) = 0.

х-¥х0 Дх-»0

127

О Примеры.

+ аппХп +

1. Линейная функция у = а1х1 + а2х2 + ... + апхп непрерывна в любой точке M(xv х2,хп) є R".

+ 2а,,х,х,, + ... + 2а,_х,х„ + 2а,,,х,,х, + ... + 2а_ ,_х_ ,х непрерывна в

2. Квадратичная функция у anxf + а22х2 +

23х2х3 + ••• + 2flB_1„XB_1X„

'пл1л2 ^ •■■ ^ ^"пллп

любой точке из R".

3. Функция f(x) = sinx непрерывна при любом х є R1. Действительно, взяв произвольно точку xQ є R1 и приращение Ах, найдем,

, откуда

x0+а г/ ■ t л , . to f Ах'

что А/(х0) sin(xn + Ах) smx0 2 sin—cos

J

Ax

lim A/(x0) lim 2sin—cos x0 +

Дх->0

Ax

= 0. •

4.20. Свойства функций,

непрерывных в точке

Г. Если функция f(M) и функция g(M) непрерывны в точке М0, то непрерывны в точке М0 и функции: &)RM)+g{M);

б) kf(M), где к — постоянная;

в) f(M)g(M);

г> ^,если£(М0)*0. g(M)

2°. Если функция f(M) определена на множестве V, непрерывна в точке М0 є КиДМд) > О (/(MQ) < 0), то существует окрестность Sr(M0) точки MQ такая, что f(M) > 0 (f(M) < 0) для всех точек Мє Sr(MQ) n V.