4.22. непрерывность сложной функции

4.22. непрерывность сложной функции

Пусть задана функция у=f{uv и2,ит), определенная на множестве Же R™. Пусть, кроме того, каждая из функций м1 =gl(x1, х2,

-' xr)> u2=S2(-xv xv •••> хп>> •••> um = Sm(xv х2> •••> Хг) определена на множестве Vc R" (см. п. 4.4).

Если функции gv g2, gm непрерывны в точке AfQ(Xj, х2, х^) є V, а функция у=f(uv и2,ит) непрерывна в соответствующей точке Р0іи°х, и°, iijj), где и° = gxiM0), и = g2iMQ), ит =8т(М<)>т0 сложная функцияу=№1х1,х2,хп),g2ixvх2,хп), gm(xv х2,хп)) непрерывна в точке MQ.

В частности, если функция и = gix) одной переменной х непрерывна в точке х0, а функция >> = /(и) одной переменной и непрерывна в точке и0 = gix0), то сложная функция у = /(g(x)) непрерывна в точке х0, т.е.

lim /(«) = lim figix)) = Д lim gix)).

129

Последняя формула, с одной стороны, показывает, что операция предельного перехода перестановочна с операцией взятия непрерывной функции (правое равенство), с другой стороны, дает правило замены переменной при вычислении пределов непрерывных функций (левое равенство).

О Примеры.

х + 1

1. lim x[ln(x +1) lnx] = lim хIn

х-н-~ х-м-~ X

= lim In

1 +

= ln

lim 1 +

= lne = l (см. п. 4.13).

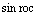2. lim

«їх -1

X = t + 1

x -> 1 => t -> 0

Sin(7t? + Jl) -SU17tf

= lim^, = lim

»-»0f2 + 2/ + l-l /(r + 2)

-lim

sin го* n

nt t + 2

v '2 2

4.23. Односторонняя непрерывность

Пусть функция у f(x) одной переменной х определена при х < xQ (х > х0). Функция fix) называется непрерывной слева (справа) в точке х0, если

Ит f(x) = f(x0) ( lim f(x) = f(x0)).

x->xq-0 x->xo+0

О Примеры.

Функция /(х) = ^ непрерывна слева в точке х0,

[О, х = О,

так как lim f(x) lim ev* = 0 = /(0).

х-ї-0 х-»-0

Функция /(х) является непрерывной на отрезке [a, b], если она непрерывна в каждой внутренней точке этого отрезка, непрерывна справа в точке х = а и непрерывна слева в точке х = b (см. п. 4.21). •

4.24. Непрерывность обратной функции

Если функция одной переменной у = f(x) строго монотонна и непрерывна на отрезке [а, Ь], то обратная функция х=g(y) опреде 

130

лена, строго монотонна и непрерывна на отрезке с концами в точках Да) и/(й).

Если функция одной переменной у Дх) строго монотонна и непрерывна на интервале ]а, Ь[ (конечном или бесконечном) и если существуют (конечные или бесконечные) односторонние пределы с lim f(x)nd= lim fix),то обратная функциях-g(y)

x-*a+0 x-¥b-0

определена, строго монотонна и непрерывна на интервале ]с, d[.

4.25. Точки разрыва функции

Пусть функция одной переменной у = Дх) определена в некоторой окрестности точки х0, за исключением, быть может, самой точки х0. Если функция Дх) не является непрерывной в точке х0, то говорят, что в точке х0 функция терпит разрыв, и точку х0 называют точкой разрыва функции.

Точку х0 называют точкой разрыва первого рода, если существуют конечные односторонние пределы /(х0 0) = lim /(х)

x->xg-0

и /(х0 + 0) = Mm fix), но /(х0 0) Ф /(х0 + 0). В этом случае наиX->Xq+0

большую из разностей между числами Дх0), /(х0 0), /(х0 + 0) называют скачком функции Дх) в точке х0.

Например, для функции fix) = —Ц7(см. рис. 4.3) точка хп = 0

1 + 2Vx

является точкой разрыва, так как в этой точке функция не определена (/(0) не существует). При этом /(-0) = Mm fix) = 1,

х-»-0

/(+0) = lim fix) = 0. Следовательно, точка хп = 0 является точкой

х->+0 и

разрыва первого рода, а разность /(-0) -/(+0) = 1— скачком данной функции.

Точку х0 называют точкой устранимого разрыва, если конечные односторонние пределы Дх0 0) и /(х0 + 0) равны между собой, но не совпадают со значением /(х0), если только оно существует.

Например, для функции /(х) = <Х ПРИХ'*2, имеем

[1 при х = 2

/(2-0) = /(2 + 0) = limxі =4, однако 4 = /(2 0) =/(2 + 0) Ф

х->2

Ф Д2) 1. Следовательно, точка х 2 является точкой устранимого разрыва функции Дх) (рис. 4.6).

131

Термин «устранимый разрыв» оправдан тем, что достаточно доопределить или переопределить функцию в точке х0 для того, чтобы она стала непрерывной в этой точке. В рассмотренном примере надо положить g(2) = 4 = lim/(x); тогда функция

х->2

] х при х Ф 2, 14 при х = 2

является непрерывной в точке xq 2.

Точку х0 называют точкой разрыва второго рода, если хотя бы один из односторонних пределов f(xQ 0) и f(xQ + 0) не существует (в частности, бесконечен). Например, для функции /(х) (рис. 4.7) точка xQ 0 является точкой разрыва второго рода, так как /(-0) = 0, /(+0) = +°°.

Рис. 4.7

Замечание. Функция л переменных}' = f(xv х2,хп) может иметь не только изолированные точки разрыва, но и целые множества точек разрывов (линии, поверхности разрывов).

имеет разрыв

Например, функция f(xux2) =

2

*2)(*1 + 3*2)

во всех точках параболы х2 = xf и во всех точках прямой 1

Хл — Хл .

2 3 1