Достаточные условия оптимальности

Достаточные условия оптимальности

4.1.

Вспомогательные математические конструкции

В ТОУ для решения задач применяется специфический математический аппарат, основанный на достаточных условиях оптимальности. Это означает, что если утверждаемое условие оптимальности достаточно, то данный управляемый процесс оптимальный. Но это не означает, что не может быть других оптимальных процессов, для которых данное достаточное условие не выполняется. Другими словами, условие А достаточно для выполнения заданного условия В, когда

Из опыта решения различных математических задач известно, что наиболее эффективным средством отыскания решений являются необходимые и достаточные условия. Однако, преподавая ТОУ уже более 20 лет, нам не удалось построить примера, где найденное оптимальное решение не удовлетворяло бы достаточным условиям оптимальности. Следовательно, хотя необходимость в общем случае не доказана, по-видимому, достаточные условия оптимальности по своей сути близки и к необходимым.

Для доказательства соответствующих теорем о достаточных условиях оптимальности введем некоторые вспомогательные математические конструкции.

Рассмотрим вспомогательную задачу оптимизации, решение которой будет использоваться в дальнейшем. Пусть задан функционал

(4.1)

u(t) = (wJ(0, иН0,...,иГ№

где x(t) — вектор состояния системы; u(t)— вектор управления.

На векторы x(t) и u(t) наложены условия

МО, і/(0) є И, /=0,1,..., 7М.

Требуется отыскать минимальное значение функционала (4.1) при заданных ограничениях.

Эту постановку можно рассматривать как частный вариант задачи оптимального управления в тривиальном случае, когда среди ограничений, определяющих множество М допустимых процессов, отсутствуют уравнения процесса.

В данной задаче нетрудно получить необходимые и достаточные условия, которым должно удовлетворять оптимальное решение (х*(0, и*(0), минимизирующее функционал (4.1). Эти условия можно сформулировать в виде теоремы.

Теорема 4.1. Для того чтобы процесс (x*(t), u*(t)) был оптимальным, т.е. минимизировал функционал (4.1), необходимо и достаточно, чтобы при всех t = 0,1,..., Т—

/°(*,**(0,и*(0)= min /°(f,jt,w).

(4.2)

Доказательство.

1. Необходимость. Пусть (х*(0, и*(0) оптимальный процесс, т.е. удовлетворяющий условию (4.1). Это значит, что

/(х*(0, w*(0)</M0, «(0)

(4.3)

при v МО» "(О) ^ Vі. Требуется доказать, что он удовлетворяет и условию (4.2).

Допустим противное: имеется такое / = т, при котором условие (4.2) не выполняется. Это означает, что при t= т существует такое значение (х(т), w(t)), что

/°(тЖ>, и(т)) </°(х^*(т), и*(т)). (4'4) Рассмотрим новый процесс (jc°(/), u°(t)), который определим

так:

(*°(f), и0 (О) = (**(0. и*(0) при f * т и (x(t), и (0) при t = т. Вычислим значение функционала (4.1) / на этом процессе:

У(*°(0, u°(t)) = XV('.**(0. "*(' )) +

+ 2? /О(г^*(о,"*(0)+/О(т,^(т),"(т)).

Разбив выражение (4.1), для J(x*(t), u*(t)) аналогичным образом получим

J (/(г), и*(0) = 5? /°(',**С ). u*(t)) + г=0

+ і' /Ои^*(0,"*(0) + /О(т,^*(т),«*(т)).

Сравним теперь правые части двух последних равенств. Первые два слагаемых в них совпадают, а третьи удовлетворяют сделанному предположению (4.4). Следовательно,

/(**(/), и*(г))>ЛА0, и°(0),

что противоречит условию (4.3) оптимальности процесса (х*(0> "*('))•

Необходимость доказана.

2. Достаточность. Пусть процесс (x*(t), u*(t)) удовлетворяет теореме 4.1. Требуется доказать, что для него будет выполнено и условие (4.1), т.е. этот процесс будет оптимальным.

Рассмотрим произвольный допустимый процесс (x(t), u{t)). Тогда из выражения (4.2) можно установить, что при V/ = = 0,1,...,7W

/°(0, jc*(0), и *(0)) < /°(0,jc (0), и (0)); /°(U*(1), «*(!)) </°(1,jc (!),«(!));

f°(T-l jc*(T -1), w*(T-1)) < f°(T-їх (Г -1), и (Г -1)). Складывая эти неравенства почленно, получим

2? /°С .**(0. и*(о) * 2? At.x (О, и (г)).

Левая и правая части в этом неравенстве — значение функционала (4.1) для процессов (/, x*(t), u*(t)) и (/, x(t), u(t))y т.е. /(/, x*(t), u*(t)) < J(t, x(t), u(t))y откуда вследствие произвольности процесса x(f), u(t)) и вытекает справедливость условия (4.1) для процесса x*(t), и*(/)), который, следовательно, и является оптимальным.

Достаточность доказана.

Изложенная теорема сводит решение поставленной задачи (4.1) к минимизации функции f°(t, х, и) при V t = 0,1,..., Т—1 по переменным (х, и) на множестве (х, и) є Vі. При этом существование минимума функции f°(t, х, и) при v t есть необходимое и достаточное условие существования решения задачи (4.1).

Отметим, что условия теоремы могут быть аналогично сформулированы и для задачи максимизации функционала, если перед ним поставить знак «минус», провести соответствующее переобозначение функций под знаком суммы и результат устремить к минимуму (см. разд. 1.2).

Теорема 4.1 может быть обобщена и на непрерывный случай, когда функционал задается соотношением

т

J = jf°(t,x,u)dt->min. (4-5) о

Однако формулировка теоремы при этом нуждается в уточнении. Что касается достаточности условия (4.2), то и в непрерывном случае это также остается справедливым (доказательство дословно повторяет приведенное выше с заменой суммирования интегрированием). Необходимым же это условие, вообще говоря, не является, что показывает следующий пример.

Рассмотрим функционал

J =jx2dt —> min, о

(4.6)

заданный на множестве кусочно-непрерывных функций jc(/), удовлетворяющий ограничению 1 < x(t) < 2. Так как вследствие указанного ограничения x2(t) > 1 при всех /, то, очевидно, и значение / не может быть меньше единицы. Таким образом, если при некотором x*(t) будет достигнуто значение J(x*(t)) = 1, то можно сделать вывод, что функционал (4.6) достигает минимального значения.

Возьмем в качестве x*(t) следующую функцию:

Очевидно, что при этом значение J(x(t)) = 1. Следовательно, x(t) минимизирует функционал /. Но данная функция, как легко видеть, не минимизирует х2(і) в функционале (4.6) при всех /

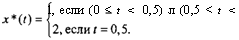є [0; 1]. В частности, этого не происходит при г = -, где значе2

ние х* = 2. Подынтегральную функцию x2(t) минимизирует значение х* = 1.

Таким образом, в данном примере необходимость условия теоремы не выполняется.

Для того чтобы условие теоремы в непрерывном случае стало не только достаточным, но и необходимым, его нужно уточнить. А именно нужно потребовать, чтобы оно выполнялось не обязательно в каждой точке t интервала [0; 7]> а за исключением, может быть, точек, значение функции в которых не влияет на величину интервала (4.5).

Возможен и другой путь. Если дополнительно наложить требование непрерывности на процесс (x(t), u(t)) и на функцию f°(t, х, и), то формулировка теоремы в непрерывном случае сохраняется дословно с заменой соотношения (4.1) на (4.5). Однако требование непрерывности (jc(0, w(0) является слишком сильным в задачах ТОУ (независимо от прикладной области) и не выполняется даже в простейших случаях, в чем мы неоднократно убедимся в дальнейшем, решая конкретные задачи оптимального управления.