Глава 2 методы оценки параметров линейных эконометрических моделей

Глава 2 методы оценки параметров линейных эконометрических моделей

Задание 2.1

Для 13 клиентов спортивного отдела магазина зафиксирована сумма покупки xt (в у. е.) и время разговора с продавцом yt (в мин.). Данные представлены в табл. 2.1.

Требуется.

Оценить с помощью МНК параметры линейного регрессионного уравнения, предположив, что переменная «длительность разговора с продавцом» объясняется переменной «величина покупки».

Оценить с помощью МНК параметры линейного регрессионного уравнения, предположив, что переменная «величина покупки» объясняется переменной «длительность разговора с продавцом».

Нарисовать диаграмму рассеяния величин (х„ yt) и обе линии регрессии. Объяснить, почему, если поменять экзогенную и эндогенную переменные местами, как правило, получаются различные уравнения регрессии.

Решение.

1. Для оценки параметров линейного регрессионного уравнения^^ Оо + ах, + є, рассчитаем сначала 16

їх, = 1 690; 2>, = 260; їх,2 = 284 100; 2>,2 = 5 392; Ех<Уг = 36 330.

-=е^=169о=ш иу=ш=т=20.

п 13 п 13

С учетом этого

Тх,у,-^у 36330-13-130-20 2>, -Зс2 284100-13-1302

«0 = у ~а2* = 20-0,0393• 130 « 14,89 . В целом, получаем

у, =14,89 + 0,0393-ж,. (1)

Оценим теперь параметры линейного регрессионного уравнения х, = ft> + A yt +

їуЇ-ту2

bo x аіу и -133,54.

Таким образом,

xt =-133,54+ 13,18-.у,. (2)

Для того чтобы можно было сравнить уравнения (1) и (2), выразим у из уравнения (2) и получим

.у, =10,14+ 0,0759-х, . (2')

Сравнение коэффициентов уравнений (1) и (2') показывает, что уравнения (1) и (2) различны (см. рис. 2.1).

у, = 10,14+0,0759 х, yt = 14,89+0,0393-x, Уі

Если рассматривать переменную у как эндогенную, а переменную х как экзогенную, то основу МНК образуют величины

л

е, (разности у,у,), если поменять переменные местами, то осл

нову МНК образуют е (разности xt-xt) (см. рис. 2.2). Минимизация суммы квадратов разностей абсцисс дает, как правило, выборочную прямую, отличную от той, которую дает минимизация разностей ординат. Прямые совпадают только в том случае, когда все пары наблюдений лежат на одной прямой, наклон которой не ноль.

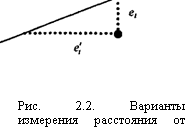Уі

х,

Задание 2.2

Имеется классическое линейное однофакторное уравнение регрессии, параметры которого оценены обычным МНК:

л

у = а0+а{х.

Требуется.

Доказать, что сумма остатков равна нулю:

Т

Л

Доказать, что у = у, среднее значение наблюдаемой зависимой переменной равно среднему значению ее оценок, рассчитанных по уравнению регрессии.

Доказать, что

т

X xtet = 0. /=1

Доказать, что

Т л

Tytet=o.

Доказать, что

У

Показать, что

D_ [L(xt-x)(yt-y)f H(xt-x)2Z(yt-y)2'

т.е. коэффициент детерминации равен квадрату коэффициента корреляции между переменными х,и yt.

8. Показать, что

t=l t=l t=l

Решение. 1.

Г Г л г Г Г

t= t= t=i t=l t=l

но из первого нормального уравнения следует, что Г г

Tyt-Щ-OiZb =0, t=l t=l

т.е. сумма остатков равна нулю.

Г л

2. В п. 1 мы доказали, что X ІУг ~ Уі) = 0 > отсюда, после де*=1

ления на Г, получим,

1 1 А

л

т.е. у = у.

Т Т л Т

Zx,e, = J,xt{yt-y,) = Zxt(yt-oq-axxt) t= t= t=

■ Z(x,yt-aQXt-axxt )= £ад-a0Zx,-ах^х,

t=A t= t=l t=

Из второго нормального уравнения получаем, что

Г г г

В целом, мы доказали, что

Y,xtet=Q. t=l

т л т т т

t,yt et = ЁС^О =«оЕег = \% -0+<h -0 = 0.

л

^ =yt + et;

^уі =Туі+ * + Tef = їу2+ 2• 0 + Те2 .

Вычтем теперь из обеих частей Ту1, учтя, что у = у и е = 0, разделим обе части на (Г-1) и получим

Итак, мы доказали, что

s2 = sl+s'2. .

у

Обозначим xt =xt х, yt -yt-y и yt =yt-y, учтя также, что у = а$ + щх , получим

S2 А

у = Ту*2 = ZOo + Щх, а0 а,Г)2 _ afe**2 =

s2~2>;2~ ъу? " z*2 ~

Z**2 _ _ 2

(z*;2) z>;2 s*

7. Согласно определению коэффициента корреляции

Л

Т.у* у* _ 5>* (ао+ъь-аосцх) _ а{^х]у,

г л У,У

Решение.

да

Txtyt

їх2

1. № = 1.ІУ, ytf =Т.(У,ах,)2 "> mm • dZiyt-ax,)2

-2Zx,(y,-axt) = 0.

Это означает, что коэффициенты корреляции г л nrXJ/ могут

У.У

отличаться только знаком, т.е. г А = гх,у •

8. Согласно п. 5 и с учетом того, что Yiixt х) = 0 , получим

2>Г = Zyf -Ы =Т,уг-1(*0 + axxtf = = Ъу1 -Ц(У ~ аУ + axxt f =

= Т.уЇ-ту2-4Txt2=Zyt2-4^,2 •

м(а)=І*Дси,+М(в,)) = а Zxf

Таким образом, а является несмещенной оценкой а. 3.

о2а =М(а-М(а))2 =М

ґ^Хі(ах,+е,) ц2Л

V

Задание 2.3

Имеется линейное однородное однофакторное уравнение регрессии

yt=ax, + s,(t=l,..., Т).

Требуется.

Вывести формулу МНК для расчета определения оценки а регрессионного параметра а.

Покажите, что оценка а, полученная МНК, является несмещенной оценкой параметра а.

Определите дисперсию оценки а.

1 Щх,е,)2

1 о

■^ZZxtxxM(stsx) = —z—

(Zx2) > ' Ы

Задание 2.4

Исследуется зависимость затрат на рекламу у от годового оборота х в некоторой отрасли. Для этого собрана информация по Т = 20 случайно выбранным предприятиям этой отрасли о годовом обороте xt и соответствующих расходах на рекламу yt (в млн. р.). Из выборки получены следующие данные: х = 17,3 ; J = 1,2; 2JW = 944,3; Z*,2 = 9250; 2>2 = 127,2. Предполагается, что зависимость у, от х, описывается следующим уравнением:

у, = ссо + щх, + є, (t = 1,..., 20).

Требуется.

Оценить параметры «ь и щ с помощью МНК.

Оценить дисперсию а} «истинной» ошибки є,.

Оценить дисперсии оценок ао и а и их ковариацию.

Решение.

л Zxtyt-Tx у 944,3-20-17,3-1,2 529,1 „А1^1.

ai — т— л — ————« и,iozi,

Ех2-х2 9250 20-17,32 3264,2

<3q = у а{х « -1,6042.

По МНК рассчитывается следующая оценка дисперсии «истинной» ошибки:

-2>f •

е Г-2'

( 529,1 ^ 3264,2

3264,2 «12,6372.

Z^=Z>?=ai2(Z^-73f2)'

«127,2-20-1,22Таким образом,

cj? = — ■ 12,6372 » 0,7021. е 18

По методу максимального правдоподобия оценка дисперсии «истинной» ошибки определяется по формуле

Она равна

ст*2 = —-12,6372«0,6319. е 20

Если не доказано, что «истинная» ошибка <?, имеет нормальное

2 *2

распределение, то оценка ае предпочтительнее, чем оценка ае . 24

«0,0995.

3. ст = а„ ■

1

„2 „2

«0,0002.

9250-20-17,3^ -17,3

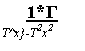
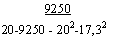0,7021

«0,7021«0,7021

■«-0,0037.

Е*2-7х2

-X

9250-20-17,3^

cov(o0,a1) = cje

2>;-7jc2

Задание 2.5

Для данных задания 2.3 установлено, что «истинная» ошибка распределена нормально.

Требуется.

Определить 95\%-е доверительные интервалы для параметров регрессии ао и СС.

Проверить, можно ли утверждать, что с вероятностью 95\% ОоєКолаїєКі, где Ко и К — доверительные интервалы соответственно параметров «ь и щ, построенные в п. 1.

Определить 95\%-й доверительный интервал для дисперсии «истинной» ошибки Є,.

Решение.

оо-х(1-а/2;Г-2).^М; ао+х(1_а/2;Г-2).СТ^^

1. Доверительные интервалы для параметров регрессии ао и «і определяются по формулам:

(2.1)

*2 *2

, (2.2)

в! -г(1-а/2;Г-2)—\%=, ах + т(1-а/2;Т-2)--^

fi? ^2

где х* =xt-x~.

Из таблицы критерия Стьюдента г (0,975; 18) = 2,101. Таким образом,

а(1-а/2;Г-2)^М = 2,101. . ^-79250 ^

^2 у20-(9250 20-17,32)

[-1,6042 0,6627-; -1,6042 + 0,6627] = [-2,2669; -0,9415]

доверительный интервал для параметра ccq.

Для нашего случая квантили распределения (0,975; 18) = 31,53 и ^(0,025; 18) = 8,23. Учитывая, что Ze,2 = 12,6372, получим для ст/ следующий 95\%-й доверительный интервал:

= [0,4008; 1,5355].

12,6372ш 12,6372 31,53 ' 8,23

а(1-а/2;Г-2)-^=== 2,101- ^°,7°21 =0,0308

yjx*2 ^20-(9250 20-17,32)

[0,1621 0,0308; 0,1621 + 0,0308] = [0,1313; 0,1929] — доверительный интервал для параметра а.

2. Если обозначить Q0 и Q случайные интервалы, реализацией которых являются доверительные интервалы Ко и К, то

Р(аоєШ = Д«ієЄі) = 0,95. Р(аоє Q0 л«! єQ0 = P{ax є Qx)-P{ccoє Qo1 axє Q0 = = 0,95-Р(аоєЄоІ«ієЄі). Поскольку всегда есть вероятность, что случайный интервал Qo не содержит параметр «ь, то условная вероятность P(oco&Qo I a\&Qi) — всегда меньше 1. Отсюда следует, что

Р(аоє0олаієШ<О,95.

Поэтому нельзя утверждать, что с вероятностью 95\% доверительный интервал Ко содержит параметр регрессии do и одновременно доверительный интервал К содержит параметр регрессии щ.

3. Доверительный интервал оценки дисперсии «истинной

ошибки» определяется по формуле

(2.3)

Х2(1-а/2;Г-2)' Х2(а/2;Г-2)

(Г-2)-а2 _ (Г-2)-а2

Задание 2.6

Для анализа зависимости целевой переменной у от объясняющей переменной х получена выборка, состоящая из Т = 50 наблюдений, и определены следующие показатели: х = 50,68 ; у = 100,44 ; Ъс№ = 290463; 2>2 = 539477. В основу исследования

положена классическая линейная однофакторная модель нормальной регрессии

у, = ссо + ctx, + st(t= 1,..., 50).

Требуется.

Проверить следующие гипотезы:

Но1: а > «ю = 1 при уровне значимости а = 0,05.

2

Н0 : «ь < «оо = 50 при уровне значимости а = 0,05.

3 2 2

Но : oi > аь = 25 при уровне значимости а = 0,05. Решение.

1 „ -ХЪУг-Ъу 290463 50 50,68-4,4 35948,04

i.a _ — _—= «и,94о/о

1 Ел^-Зс2 166314 50-50,682 37890,88

Ъе} =Ъу1 -Ту2 -а1{^х2-Тх2)*

* 539477 50 ■ 100,442 94872 • (166314 50 • 50,682 ) « «964,336.

— 964,33*4,4822. 48

Задание 2.8

Таким образом,

T = h-aio|^lj0;9487-l^i663i4_5() g2g з сте У ' 4,4822 V

Табличное значение 95\% квантиля распределения Стьюден-та с 48 степенями свободы равно г (0,95; 48) = 1,68. Поскольку 2,23 > 1,68, то нулевая гипотеза Но1: щ > «ю = 1 отклоняется при уровне значимости а = 0,05.

2.

а0 = у сцх * 100,44 0,9487 • 50,68 и 52,366. Теперь вычислим

K-flbol рТ>У* _ [52,36-501 Г-дб6314-50-50,682; { ?£ ае І I*2 4'4822 * 166314

2

Поскольку 1,78 > 1,68, то нулевая гипотеза Но : осо< Ооо = = 50 отклоняется при уровне значимости а = 0,05.

3. Сначала рассчитаем

Учтем, что для числа степеней свободы больше 30 функция случайной величины w, распределенной

по закону может быть аппроксимирована стандартным нормальным распределением:

z = 72-38,57 -795 «-0,96.

3 2 2

Поскольку -I,96<z=-0,96<1,96, то гипотезу Н0 : ае >оь =25 нельзя отклонить при уровне значимости а = 0,05.

Имеется нелинейное однофакторное уравнение регрессии:

a

у, = — + г,.

Требуется.

С помощью МНК оценить параметр регрессии а.

Рассмотреть линейное однофакторное уравнение y't = = a'xt + \%t, где y't = 1у, и a'= I/а, и установить, какое соотношение существует между случайными ошибками <?, и

С помощью МНК рассчитать оценку а' параметра регрессии а' и сравнить ее с оценкой из п. 1.

На основе трех пар наблюдений (xh у,) — (4; 2,5); (2; 5); (10; 1;25) — показать, что оценки из пп. 1 и 3 в общем случае не совпадают.

Решение.

1. Для определения оценки а параметра регрессии а минимизируется функция

№ = Z(yt-y,)2 = I.

Ґ . Л2

Уг

-1 = 0.

a

Уг

V xt J

v xt J

da

Отсюда следует, что

a = :

ЪУг<хг El/*,2

Функция j{a) является параболой, ветви которой направлены вверх, поскольку ее квадратичный член имеет положительный коэффициент £1/х,2. Таким образом, при данном значении а действительно достигается минимум функции.

Если выражение у', ах, + g, преобразовать, подставив вместо y't = lyt и учтя, что а'= 1/а, то получим, что

в

' a'xt(a'xt +E,t)

При определении оценки а'параметра а'преобразованного уравнения регрессии^', = а'х, + минимизируется функция

f(a') = Z(y't-y't)2=Z(y't-a'xt)2.

,_Zxty't = Цх,/у, Zxf Zxf

да'

Отсюда получаем, что а

Функция Да') является параболой, ветви которой направлены вверх, так как при ее квадратичном члене стоит положительный коэффициент 2JC,2. Поэтому при а' действительно достигается минимум функции.

В общем случае

Задание 2.9

Имеется выборка, состоящая из Т= 6 пар наблюдений (х,, у,): (2,0; 0,0); (2,5; 0,5); (3,0; 1,0); (4,0; 1,0); (4,5; 0,5) и (5,0; 0,0), которая характеризует особый случай представления данных.

Требуется.

Нарисовать диаграмму рассеяния и выяснить, о каком особом случае идет речь.

Построить регрессионное уравнение для этого случая и прокомментировать его.

Рассчитать коэффициент детерминации и проинтерпретировать его.

Определить, что изменится, если принять, что первые три и последние три пары значений относятся к разным генеральным совокупностям.

Решение.

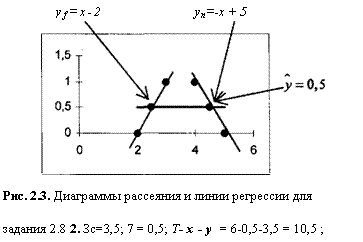
На рис. 2.3 изображены диаграммы рассеяния имеющихся пар наблюдений. Очевидно, что первые три пары лежат на одной прямой, а последние три пары наблюдений — на другой прямой.

т.е. оценки параметра а различны.

4. Величины, необходимые для расчета оценок а к а' представлены в табл. 2.2.

Таблица 2.2

3,25 0,3225

а' = « 0,0833 и соответственно — = = 12, т.е. а ф —

120 а' 10 а'

ХЗД =1,25 + 3 + 4 + 2,25 = 10,5.

Поскольку Y,xtyt =Т-х-у, то ах = 0 и а0=у = 0,5. Прямая, параметры которой оценены с помощью МНК, проходит паралл

лельно оси х, у = 0,5 . Это означает, что эндогенная переменная у в случае линейной однофакторной регрессии не зависит от экзогенной переменной х.

Поскольку Y,xtyt ~Т'Х-У, то коэффициент детермина-ции R = 0. Это означает, что дисперсия ау значений эндогенной переменной равна дисперсии остатков ае2 и, таким образом, регрессионное уравнение не объясняет изменчивость наблюдаемых значений у,. Рис. 2.3 показывает, что коэффициент детерминации может принимать значение 0, несмотря на то, что существует определенная (нелинейная связь) между переменными у, и xt.

Если исходить из того, что первые три и последние три пары наблюдений относятся к различным генеральным совокупностям, то построим для каждой из этих групп отдельно регрессит-г л л

онные уравнения. При этом получим; ух =х-2 и уп = -х + 5, (см. рис. 2.3). Поскольку все пары значений обеих групп данных лежат на соответствующих линиях регрессии, то Я2 = 1, т.е. изменчивость эндогенной переменной полностью объясняется рассмотренными уравнениями регрессии.

Задание 2.10

Рассмотрим линейную однофакторную регрессионную модель, в которой экзогенные переменные принимают только два значения — 0 и 1, т.е. являются индикаторами.

Требуется.

1. Определить общий вид уравнения регрессии.

2. Для 30-летних коммерсантов с высшим образованием объяснить уровень месячного дохода с помощью переменной «пол», если для 6 случайно выбранных женщин ежемесячные доходы составляют 3 750, 3 910, 4 230, 3 890, 4 090, 4 130, а для 6 случайно выбранных мужчин — 4 850, 3 950, 4 210, 5 580, 5 170 и 4 740. Построить соответствующее уравнение регрессии.

Решение.

1. Линейное однофакторное уравнение регрессии с переменной-индикатором в качестве экзогенной переменной представляет собой частный случай линейной однофакторной регрессии, и требуется внести некоторые дополнения в общую процедуру оценки параметров уравнения. Обозначим Т и 7о число пар данных, в которых соответственно х = 1 и х = 0. Кроме того, у и у2 — средние значения переменной у, для которых соответственно ї=1их = 0.р = Тх/Т — доля пар данных, для которых х = 1. Получим

х = ^2>, = р; у = р■ у + (1 -р) ■ уо;

Zxtyt= £ Уі =т-у = т-р-у\;

t:xt=

Ъ*2=тх=т-Р.

Таким образом, оценки параметров определяются по следующим формулам:

Т-р-у-Т-р-у _ ух-у Т-р-Т-р1

У~У

а0=у— р.

1-р

Итак, получим уравнение

1-р

-р

-Zyt—±-— Z л

Отсюда вытекает, что при х = 1, ух = у, а при х = О, (-р)-у-р-у + р-у

т г.

1 tJC,=l

1-р 1-р 1

Это означает, что оценки при экзогенных переменных-индикаторах принимают два значения (0; у0) и (1; у1).

2. Уо = 4000 и = 4750, т.е. имеем точки (0; 4000) и (1; 4750).

Задание 2.11

Имеется линейная классическая нормальная модель множественной регрессии

уt «ь + сад, + ... + а„ х„, + є,.

Требуется.

Рассмотреть функцию плотности распределения вектора «истинной» ошибки є и показать, что из того, что вектор є имеет нормальное Г-мерное распределение, следует, что отдельные ошибки є, (t = 1,2,...,Г) являются независимыми друг от друга и нормально распределенными с параметрами М[є,] = 0 и D[s,] = а}.

Определить, как распределен вектор эндогенных переменных у, и какова функция плотности распределения этой переменной.

Показать, что вектор оценок о, полученный обычным МНК, является оценкой максимального правдоподобия для а.

4. Определить, как распределен вектор оценок о, и какова функция плотности распределения этого случайного вектора.

Решение.

/z(z;n;V)=1. Функция плотности распределения произвольного Г-мерного нормально распределенного вектора z запишется следующим образом:

1

Т

(л/2Їх) ^det V

expKz-iO'V-Vu)}, (2.4)

где jj—математическое ожидание, v— ковариационная матрица. Ковариационная матрица Z вектора ошибки є имеет следующий определитель:

det(2) = det(oi2£) = (оіУ det(E) = <j?T.

Обратная к ковариационной матрице X—

{2>х = {?їе? = е.

1

1

С учетом того, что М[є] = 0, из выражения (2.4) вытекает

ЄЄ,

CTCV27C

fE(s,0;czsE) =

у

)

с

2ai

l £

ехЫы =п

expi

expi

Ос*$2п

1 ы.

2<т| /=і t= <уе V 2л 2<т| t=i

т.е. функция плотности распределения f£ вектора ошибки є образуется путем перемножения Т функций

2 ч

1

2ст;

fAet'&ae) = 7==-ехР

C7pV27t

Таким образом,

$Rn-i fE (є, 0; cj2£')d(e1,..., eM, et+1,..., eT) =

T

= JRn-l П f£T (ST> CTE Жв1' • • • > Et-1. Et+1> • • •' ЄТ ) = T=l

T

= /є,(єг' °> al) ■ iR"~l П /єт (st >°; стє )d(el' • • •' et-h et+l. • • • > eT ) =

T=l

= /Є((вг,0;а2)-1 = /Е((єг;0;а2).

Очевидно, что 0; а2) представляют собой функции

плотности нормального распределения с параметрами /л = 0 и о2 = ст/. Отсюда следует, что отдельные ошибки є, (t = 1,2,...,7) независимы друг от друга и нормально распределены с параметрами М[є,] = 0 и D[st] = сг2.

2. М[у] = М[Ха+є]= М[Х-а] + М[є] = Хсс

Щу] = D[X-a+ є] = D[s] = <те2Е.

, С учетом выражения (2.4) функция плотности распределения у представляет собой

1

fy(y;Xa;alE):

ехр^-^Іу-ХаУіу-Ха)^

4. Вектор оценок параметров о рассчитывается как линейная комбинация вектора эндогенных переменных^:

а = (ХХ)Л-Ху.

Так как согласно п. 2 вектор у имеет Г-мерное нормальное распределение, то вектор оценок а имеет (и + 1)-мерное нормальное распределение с математическим ожиданием М[о] = а и ковариационной матрицей Cov[o] = а2(ХХ)'х.

Определитель ковариационной матрицы равен

det(Cov[a]) = det(cj2 • (XX)~l) = (ст2)"+1 • det((XX)~l) =

= g2(w+l) 1

й&((ХХу1) '

а обратная к ковариационной матрице определяется следующим образом:

(СоуМГ1 = (а2 • (ХХУ1)'1 = ■ (XX) .

Итак, функция плотности распределения вектора оценок а может быть представлена как

fa(a;cr,a£2iXX)-l) =

3. Рассмотрим функцию максимального правдоподобия

I 2

L(aX, у, <7е ) для вектора параметров а при фактических данных (X, у) и данной дисперсии ошибки сг2.

L(ax,y, а2)=^;Х<х, а2Е).

Поскольку плотность распределения fy является экспоненциальной функцией с отрицательной экспонентой, то функция правдоподобия, как функция а, достигает максимума только тогда, когда произведение (у-Ха)'(у-Ха) минимально. А вектор о как раз и определяется, исходя из минимума этого произведения, т.е. он является оценкой максимального правдоподобия для а.

Задание 2.12

Имеется классическая линейная модель множественной регрессии, записанная в отклонениях

у* = щхи + ... + апХп' + є,* (ґ= 1,..., Т),

где yt=y,-y;

* — xit ~ xit ~ xi ('" ~ І»—»")»

1 т т у = -і.уґ> */ = 2>i»; 11= t=

є, — стохастическая ошибка. Требуется.

Показать, что форма этой модели эквивалентна форме классической линейной модели множественной регрессии

у,= Of, + «1 хи+... + є,.

Определить вектор оценок параметров а = (а ап*)'.

Построить ковариационную матрицу вектора оценок а .

Решение.

1. В случае классической линейной модели множественной регрессии имеется Г уравнений

у,= ао + ах хи+ ... + а„х„,+ є, (t = 1,...,7). (2.5)

Если сложить эти уравнения и их сумму разделить на Т, то получим следующее уравнение:

у = o.q + aixj +... + апхп + є , (2.6)

1 т

где у=-Ъу( ;

1 t=l _ 1 Т

11= і т

є=-Іє,.

1 ы

Теперь вычтем уравнение (2.6) из каждого из Т уравнений системы (2.5):

Уі ~У = al(xlt ~*i) + • • • + an(xnt -*и) + (et є) (t = ,...,T). Если обозначить теперь у* =yt -у; x*it -хн -х, (і = 1,...и); є* = st є, то получим

у* = ад,' + ... + а^п* + є* (t = 1,..., 7), т.е. классическую линейную модель множественной регрессии в отклонениях.

2. Для определения вектора оценок параметров а должна минимизироваться сумма квадратов остатков

£е;2 = е/ = (у'-Х>а'у(уг-Х,а)=уУ-2а'Ґ'у + а'Ґ'Ґа

* *

относительно переменных а ап .

Необходимым условием минимума функции е '-е является равенство нулевому вектору вектора частных производных

д(е'е)1да=-2ЯҐ'-у + 2Ґ'У а = 0.

Отсюда получаем так называемую редуцированную систему нормальных уравнений

Решив эту систему уравнений относительно а, имеем а =(У'У)-1У'-/.

Так как £ et квадратическая функция относительно о ,

t=l

причем коэффициент при ее квадратическом члене положителен, то при о достигается ее минимальное значение, т.е. вектор о — вектор оценок, который и требовалось определить.

г

3. Сначала обратим внимание на то, что £ (xit -*,•) = Ob для

t=

всех / = 1,..., п.

Х*'-е=Х*'-(е-е) = Х*'-е-Х*'ё = ^'•e-(eE(xlt-x1),..,eZ(xmt-xn))' е.

С учетом этого

a = (Л*' Л*)"1 AV = (Л*' У)'1 У'(У а + е) = = а + ( У' У)"1 aV = a + ( Л*' А^1 Л*'-е.

Математическое ожидание вектора оценок а М[а] = М[а + (X*' ХУ Х*'-е] = а + (X*' х'у1 Х*'-М[е] = а,

т.е. а' обладает свойством несмещенности.

Ковариационная матрица вектора оценок а —

Cov(a') = М[(а-а )-(а-а)'] = = М[((Х*' х'у1 Х*'-еН (X*' Х*у1 Х*'-е)'] = = М[(Х*' Х')'1 х''-е-е'X* (X*' х'у1] = = (Х'' X*)'1 х''-М[е-е']-X* (X*' X*)'1 = = (X*' Х'у1 х''-ае2-ЕX' (Х'' Х'у1 = ае2-(х'' X*)'1.

Задание 2.13

Имеется классическая линейная модель множественной регрессии, записанная в отклонениях

у* = аххи +... + ОгХм + Ь (t = 1,..., Т). Требуется.

Показать, что для значений а^щ = ( аа„)' выполняется следующее соотношение:

аф) = (Х''хУх''-у'.

Показать, что значение может быть определено по следующей формуле:

а0 = У-в(0Г*>

ГДЄ х = (х1,...,х„).

Решение.

1. Нужно показать, что Я(0) = {аап)', т.е. оценка вектора а

без его первой компоненты, может быть рассчитана на основе

* * матрицы отклонений X и вектора отклонений у согласно выражению ада = (X 'хУх*'-у*. Другими словами, что вектор оценок

40 ада совпадает с вектором а (вектором оценок параметров классического линейного уравнения множественной регрессии, записанного в отклонениях).

Вектор а удовлетворяет системе уравнений

(2.7)

ут = ао +ахіт +... + апхпТ+ет

Если сложить эти уравнения, разделить сумму на Г, учитывая при этом, что ё = 0, то получим

у = uq + ajjcj +... + апхп .

После вычитания этого уравнения из каждого уравнения системы (2.7) имеем следующую систему уравнений:

(yl-y) = al(xn-xl) + ... + an (хп1 хп) + ех;

(yT-y) = ao+al(XlT-xl) + ... + an(xnT-xn) + eT.

В матричной форме записи —у* = X* + е. Матрица X определяется следующим образом:

хи .
Kxlt ■	• X у
хи .	.. хп1У
Kxlt •	■• Xlty

X* ~ -^(О) ~ X >

где X,

(0) =

*(0) = Таким образом.

Х'*-е-(х{0)-Х'Уе = Х10уе-Х'-е =

t

= X[0ye-(xlYJet,...,xnJJet) = = X{Qye = Xl0y(y-X-a) = Xl0yy-Xl0yX-a.

Но из системы нормальных уравнений следует, что

Х(р) • у = Хф) ■ Ха.

Итак,

Х*'е = 0.

С учетом этого получим

(X*' X*)-1 Ґ: / = (X*' X*)'1 X*'(X* а(0) + е) = = а(0) + (Х*'Х*у1 Х*'-е = Офу

2. Первое уравнение системы нормальных уравнений выглядит следующим образом:

Т ■ а0 + а{£ки + + anYxnt = 2>*. Решив это уравнение относительно а0, получим \% =У-аХ-■■■апхп =у-а[0ух.

Задание 2.14

Экзогенные переменные линейного уравнения множественной регрессии претерпевают следующие преобразования:

р _ х ~с\ . . р хп ~сп

с21

*1 =

с2и

Показать, как изменятся МНК-оценки ащ ~ {а,..., а„)', если от исходных экзогенных переменных перейти к стандартизованным переменным.

Показать, что для ковариационной матрицы вектора оценок O(of выполняется следующее соотношение:

Cov(amp) = C1-Cov(a(p)).

Показать, что в результате такого линейного преобразования не меняется оценка дисперсии ошибки.

Решение.

1/^21

о

с11

1. Матрица С как диагональная матрица обращается следующим образом:

о ^

С1 =

1/с2и

Если обозначить как

то для преобразованной матрицы X@f (матрицы факторов без первого столбца) получаем

где с1(єіг, с2,*0,/ = 1,..., и.

Требуется.

1. Показать, что МНК-оценки параметров регрессии О(0)Р = (ар,..., а/)' после таких преобразований определяются по следующим формулам:

0

с1п.

с2

о

Я(о)Р = С ■ а(0),

(с21 ... 0^

где С

~{х(0) ~с)с

Хр А(0)

(хп-сп)/с21 ... (х„1~сы)/с2п (xlt-сп)/с21 ... (xnt-с1п)1с2п

Соответствующая матрица ХР со средними значениями столбцов согласно свойству линейности среднего арифметического имеет следующий вид:

Хр =

'(*ц-сп)/с21 ••• (хп1-с1п)/с2пл

х-схс(xlt-сп)/с2і ... (xnt-сХп)1с2п

Таким образом, имеем следующую матрицу А^* преобразованных (центрированных) значений экзогенных переменных:

уР* уР _ уР —

= (Хф)-С1)-С-1-(Х-С1)-С~1 = = (Х(0)-Х)-С-1=Х*-С'1.

Теперь определяем МНК-оценки:

аР0)=(ХГ*'.ХГ*Г1.ХР*'у =

= «г1.х"х'-с-1г1-с-1-х"у =

*' * 1 1 *' *

= С-(Х X )~1-С-С~-Х у =С-а(0).

Этот результат означает, что МНК-оценки параметров линейного уравнения множественной регрессии, т.е. а(о) , зависят от единиц измерения, в которых измерены экзогенные переменные.

2. Стандартизованные экзогенные переменные определяются по следующей формуле:

s _ xi xi

Xj

1 т

где *,-=-2>й , 1 t=l

*/ = ^ I (\% xf)2 , I = 1,..., п.

Очевидно, что стандартизация является линейным преобразованием экзогенной переменной

CU =Xt И С2, = $,(/ = 1,..., П).

Согласно п. 1 оценка параметров регрессии после стандартизации экзогенных переменных —

af = sr а, (/= 1,п).

Итак, оценка /-го параметра регрессии после стандартизации экзогенных переменных получается путем перемножения соответствующей оценки до преобразования на стандартное отклонение наблюдаемых значений /-й переменной.

Согласно решениям задач 2.12 (п. 3) и 2.13 (п. 1)

Cov(fl(o)P) = cгe2•(A*,*'•^*)-1.

Учитывая, что

хГ=х*-сполучим следующую ковариационную матрицу оценок параметров:

Cov(a(0f) = а2 ■ (СГ1 ■ X'' • СГ1)'1 = а2-С(X*' ■ Х*Т1 ■ С = = СГ • а2(Х'' ■ ХУ = С2 • Cov(a(0)).

Для вектора остатков выполняется следующее:

<? =/ Л"* а(0)р =у'-X* ■ СГ1 ■ С ■ а(0) = /-X* ■ а(0) = е.

Из равенства векторов остатков / ие непосредственно следу-ет, что линейное преобразование данных не изменяет оценок ае.

Задание 2.15

Изменение спроса на некоторое благо (у) у домашних хозяйств определенной структуры можно объяснить с помощью цены этого блага (хх) и дохода домохозяйства (х2)Соответствующая информация представлена в табл. 2.3.

Требуется.

1. Оценить с помощью МНК параметры линейного двухфак-торного уравнения

у,= ао + «і хи+ аг х2 + st и интерпретировать оценки.

2. Оценить дисперсию ошибки сг£ .

л

3. Рассчитать оценку математического ожидания у при

xi = 5,5 и х2 = 980.

Z*k Hx x2t

Решение.

1. а{0)=(Х Х)1Х у

ґ -*2 "* * ' » *

ТхьУі

ЪХЪУ*;

<>0=у-а(0)х

Рассчитаем сначала у = 30,84 ; х = 4,35 ; л:2 = 1041. Теперь определим

1*1? =і4-Щ2 =(4Д2 +... + 4,82)-10 4,352 = = 190,47 -10 ■ 18,9225 = 1,245;

Х42 =6090; 2>1?*22 =9,5; Е^2^ =-1,64; =126,6. Таким образом, получаем

_f 1,245 9,5 У1 Г-1,64 _t 9,5 6090J 126,6

= 1 Г6090 -9,5^ Г-1,64^ ( -1,4937 ^

1,245-6090-9,521-9>5 1,245J 126,6 J ^ 1^0,023118J '

ао = У-аіХі-а2Х2й,13>271Итак, уравнение регрессионной гиперплоскости выглядит следующим образом:

у = 13,271 -1,4937*! + 0,023118х2 •

Значение й и -1,5 говорит, что при повышении цены на 1 единицу спрос на благо в среднем при прочих равных условиях падает на 1,5 единицы,

Значение а2 « 0,02 показывает, что при увеличении дохода на 1 единицу спрос на благо в среднем при прочих равных условиях увеличивается на 0,02 единицы.

При выполнении предпосылок классической линейной регрессионной модели оценка

2 1 х2 1 х2

T-n-l 1

является оценкой а?Так как Я(0) = (X* X*)~l X*у*, то получаем

Ее,2 = ё ■ е = О*-X' • а(0))'О*-X* ■ в(о>) = =/' ■ у*-2а