2.6.2. двухшаговый метод наименьших квадратов
2.6.2. двухшаговый метод наименьших квадратов
Мы фактически уже воспользовались этим методом в разделе 2.3 при рассмотрении системы C = a+fiYt + et,
[Yt = C + It.
Там мы подменили переменную Yt в первом структурном уравнении
искусственной инструментальной переменной Yt =у + S It, где у и
S оценки наименьших квадратов, получаемые при оценивании модели Yt = у+ SIt +et. После такой подмены уравнение
Ct = а + pYt + et состоятельно оценивается обычным методом наименьших квадратов, поскольку "объясняющая переменная" Yt в этом уравнении не коррелирована с et.
Пусть мы имеем систему g одновременных уравнений = + ut, t = n,
где
Ги —
г = і о
SS J
Б:
ви вк1
... в
Kg )
 yt = Уа,-, ytg) t -м наблюдении,
yt = Уа,-, ytg) t -м наблюдении,
xt =(xti,-, ) вектор переменных в t -м наблюдении,
ut =(ut1, — , utg) вектор значений случайных ошибок в t -м
наблюдении, и при этом предполагается невырожденность матрицы Г. Пусть наибольший интерес представляет первое уравнение системы. (Это не уменьшает общности, поскольку уравнения всегда можно надлежащим образом перенумеровать.) Считая, что первое уравнение нормировано на коэффициент при переменной yt1, уединим эту переменную в левой части, преобразуя уравнение к виду:
JKX,1A tKi + Ut1,
или
где
вектор значений g1 эндогенных
yti = ^ti«i + XA + utl,
Yt1 ={yt1, — ■> ytg1 ) u^iKi^jj оііч-і^ііігіігі 6i
переменных, включенных в правую часть первого уравнения, Xt1 = (xfi, —, x*K ) - вектор значений K1 предопределенных
переменных, включенных в правую часть первого уравнения, а1 и в1 векторы коэффициентов при эндогенных и предопределенных переменных, включенных в первое уравнение. Состоятельному оцениванию коэффициентов уравнения мешает эндогенность переменных у*л, — ,y*g . Это затруднение преодолевается за два шага
(отсюда название метода: двухшаговый метод наименьших квадратов, 2SLS two-step least squares, two-stage least squares).
1. Производится оценивание уравнений регрессии каждой из
этих переменных на все предопределенные переменные,
включенные в систему. В качестве очищенных вариантов
переменных Уд,...,y*g берутся предсказанные значения
y *t1,..., y * g этих переменных. (В этом контексте
предопределенные переменные понимаются как инструменты для очистки эндогенных переменных.)
2. Значения y*a,...,y* g эндогенных переменных в первом
уравнении заменяются значениями yy* g . Полученное уравнение оценивается методом наименьших квадратов.
Как и в случае оценивания обычным методом наименьших квадратов (OLS) единственного уравнения в линейной множественной регрессии, процедуру 2SLS можно представить в матричном виде. Для этого будем предполагать, что в левой части i -го стохастического структурного уравнения находится единственная эндогенная переменная yti, и обозначим:
Уі = (Уи, — ,yni J вектор-столбец значений i -й эндогенной переменной в n наблюдениях,
матрица значений в n наблюдениях gi
УгА — У ngi J
эндогенных переменных, включенных в правую часть i -го уравнения,
(x х Л
матрица значений в n наблюдениях Ki
х
nl
х
nK
і J
предопределенных переменных, включенных в правую часть і -го структурного уравнения,
вектор-столбец значений ошибки в і -м
структурном уравнении в n наблюдениях,
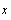
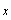 11 "4K
11 "4K
X
матрица значений в n наблюдениях всех
V Xn1
х
nK J
K предопределенных переменных, включенных в систему,
1g
п1
И:
матрица коэффициентов приведенной
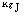 | |||
 | |||
1g
w1
W
матрица значений в n наблюдениях
ng J
ошибок в g уравнениях приведенной формы. (Заметим, во
избежание ^гашші^ что уг ={Уl1,к,yn,Т и иг =(ыь.,к,Т -векторы-столбцы, содержащие значения объясняемой переменной и случайных ошибок в -м структурном уравнении в моменты времени t = 1,■..,n. Их не следует путать с ранее использовавшимися векторами-строками yt = (yt1, ■.., ytg) и
Ut = (Ut1, , Utg , содержащими значения объясняемой переменной и случайных ошибок в g уравнениях, относящиеся к одному и тому же моменту времени t .)
Тогда первый шаг процедуры 2SLS оценивания і -го структурного уравнения состоит в оценивании методом наименьших квадратов отдельных уравнений системы
Y = XU, + W,
где Пі подматрица матрицы П коэффициентов приведенной формы, образованная теми ее столбцами, которые соответствуют эндогенным переменным, включенным в правую часть і -го структурного уравнения, а W подматрица матрицы W, образованная столбцами матрицы W, соответствующими тем же эндогенным переменным. Оценив отдельные уравнения методом наименьших квадратов, мы получаем оценку Пi матрицы Пі и на
ее основе оценку матрицы Yi в виде Yi = ХП i. Матрица Yi содержит значения эндогенных переменных, включенных в правую часть і -го структурного уравнения, "очищенных" от корреляции с ошибкой в этом уравнении.
Обозначая а{ и в{ векторы коэффициентов при эндогенных и предопределенных переменных, включенных в i -е структурное уравнение, запишем это уравнение в виде:
Уі = Yfld + Хгвг + щ = 2г6г + щ,
где
v3v
Z, =[Yt X, ].
е в следующей ф
((y Yі )a+ u,),
y, = Ytat + X tet + пг = Ytat + Хгвг +
Мы также можем записать это уравнение в следующей форме:
+щ
или
У і = ZA+Єг ,
где
Второй шаг процедуры 2SLS состоит в вычислении оценки наименьших квадратов вектора 8І в последнем уравнении. Эта оценка вычисляется по обычной формуле:
srLS = (zfzf)ҐZfyt. ^ ^
При этом, естественно, требуется, чтобы матрица Zf Zf была невырожденной. Заметим, что rank (zf Zf )= rank Zf < rank X . Но матрица Zf Zf имеет порядок, равный gt + Kt, а rank X = K, так что необходимо, чтобы K > gi + Ki, т.е. K Ki > gi = (g g*)-1, а это есть не что иное, как известное нам порядковое условие идентифицируемости. Для состоятельности S2SLS требуется еще, чтобы предельная матрица
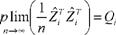
имела конечные элементы и была невырожденной, а для этого матрица П. должна иметь полный столбцовый ранг. Последнее же выполняется в случае идентифицируемости i -го уравнения (см. [Schmidt (1976), p. 150-151]).
Хотя на втором шаге используется OLS, непосредственное использование для построения t -статистик и доверительных интервалов вычисленных (по формулам OLS) значений стандартных ошибок коэффициентов невозможно. Эти значения должны быть скорректированы. Например, если дело касается первого уравнения, то на втором шаге оценивается уравнение
yti = aiiу а + — + ag 1,i ytg 1 + xn + — + 0Kl,i xtK1 + "t^
где yt*, —, ytgg очищенные на первом шаге значения эндогенных
переменных. При вычислении стандартных ошибок коэффициентов по обычным формулам OLS используется оценка дисперсии случайной ошибки в правой части уравнения в виде: ~2 = i= ;
n g1 K1
вместо этого следует использовать другую оценку:
S2 = ,
n g1 K1
в которой вместо "очищенных" значений yt*,...,ytg используются "сырые" значения Уд, —,ytg .
В обеих формулах оценки параметров получены методом 2SLS; для сокращения записи в обозначениях этих оценок опущен верхний
индекс, указывающий на 2SLS (например, а11 вместо ). В
специализированных программах статистического анализа систем одновременных уравнений такая коррекция предусмотрена.
З а м е ч а н и е 1
На втором шаге 2SLS не следует особенно полагаться на указываемые в распечатках значения t -статистик, поскольку если данных мало, то асимптотическая теория неприменима и эти статистики не имеют ни нормального, ни t -распределения. Напротив, статистики, получаемые на первом шаге, имеют t -распределения при нормальном распределении ошибок. Однако они не предназначены для выяснения значимости отдельных коэффициентов.
З а м е ч а н и е 2
Вернемся к рассмотренной ранее системе
JQt = °о + a1Pt + ut,
[Q, = Ь0 + b1Pt + Ь2 Pt + b3St + Vt,
в которой, как мы установили, первое уравнение сверхидентифицируемо. Следуя методу инструментальных переменных, мы могли бы произвести "очистку" эндогенной переменной р в правой части первого уравнения, используя в
качестве инструмента только одну из переменных Rt и St. В 2SLS в качестве инструментов для очистки Pt используются сразу обе эти переменные. Очистка с использованием только одной из этих переменных также приводит к состоятельной оценке, но эта оценка менее эффективна (ее асимптотическая дисперсия больше, чем у оценки, полученной с применением пары инструментальных переменных). В этом смысле 2SLS оценка является наилучшей инструментальной оценкой среди этих трех альтернатив.
З а м е ч а н и е 3 (Проверка адекватности)
Получив в результате применения двухшагового метода наименьших квадратов к i -му структурному уравнению оценку
S2SLS, мы получаем далее оцененное значение y2SLS = ZiS2SLS
вектора yt и вектор остатков u2SLS = yi — y2SLS. (Заметим, что эти остатки отличаются от остатков, непосредственно получаемых на втором шаге 2SLS и равных yi — ZiS2SLS .) Опираясь на эти остатки, можно обычным образом проверять адекватность этого уравнения, используя критерии:
нормальности (Харке-Бера, по оцененным асимметрии и куртозису последовательности остатков);
линейности (добавляя степени и перекрестные произведения предопределенных переменных и проверяя гипотезу зануления коэффициентов при "лишних" составляющих);
гомоскедастичности (Уайта, Пагана-Холла);
независимости против автокоррелированности остатков (Бройша-Годфри).
При обнаружении нарушений стандартных предположений необходимо соответствующим образом изменить спецификацию модели или, не изменяя спецификации, скорректировать статистические выводы.
З а м е ч а н и е 3a
Критерий Пагана-Холла предназначен специально для выявления гетероскедастичности в отдельном уравнении системы. В отличие от других критериев гомоскедастичности, он не предполагает отсутствия гетероскедастичности в других уравнениях системы. Этот критерий реализован, например, в пакете Stata.
2.6.3. GLS-оценивание систем одновременных уравнений. Трехшаговый метод наименьших квадратов
Если нас интересует оценивание коэффициентов всех g структурных уравнений, и каждое из уравнений идентифицируемо (идентифицируемо точно или сверхидентифицируемо), то тогда мы
можем сразу получить OLS-оценку П матрицы коэффициентов приведенной формы системы и на ее основе сформировать
подматрицы П1, ■.., П g, соответствующие эндогенным переменным,
включенным в отдельные уравнения структурной формы y, = У,щ + X Д + и, = ZД + и,, і = 1, к, g .
После этого можно вычислить Yt = ХПt и получить 2SLS-оценку
£2sls для д , применяя OLS к уравнению y t = Zt Д + et.
Совокупность оценок <!>.2SLS, , = 1,к,g , в форме вектора
(g2sls
2sls =
C2SLS
КД J
фактически получается как OLS-оценка уравнения регрессии
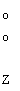
V yg J
о о о о
| + | ||
| V g J | V g J |
gJ
в сокращенной форме y = ZS + є,
где
| 8" | ' є 1 | ||
| , 8 = | , є= | ||
| V g J | V g J |
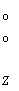 о
о
о z2
y
gJ
V yg J
о о —
V
Соответственно, вектор 82SLS находится по обычной формуле:
82SLS =(z tz Jz Ty.
Эта оценка неэффективна вследствие коррелированности ошибок єл,...,є1\% (имеющей место даже при некоррелированности ошибок
ut1, —, ug в структурных уравнениях) и различия матриц —, Zg .
Эффективную оценку можно было бы получить, используя здесь вместо OLS обобщенный метод наименьших квадратов, (GLS), но для этого надо знать ковариационную матрицу вектора є. Поскольку же эта матрица неизвестна, мы можем довольствоваться только ее оценкой, и такая оценка должна быть состоятельной, если мы хотим получить в итоге асимптотически эффективную оценку вектора 8.
Заметим, что ковариационная матрица вектора є при наших предположениях имеет весьма специфический вид:
11
nl
Cov(e) = Cov м
-ig
| — Vg 1 | ||
| л221* | ||
| ig 2 Ig |
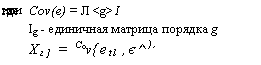
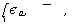
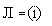 ковариационная матрица вектора єа,..., etg t
ковариационная матрица вектора єа,..., etg t
Л <8> Ig формализованное обозначение матрицы, являющейся
кронекеровским произведением матриц Л и Ig .
Таким образом, для реализации доступного GLS необходимо состоятельно оценить ковариации itj . Это можно сделать, используя
для Xtj естественную оценку
2SLS
і, = 1(йГ )Ти2 n
Заменяя в выражении для Cov(e) истинные значения оценками і,, получаем состоятельную оценку ковариационной
матрицы Cov(e) в виде Л <8> Ig . В результате приходим к доступной
обобщенной оценке наименьших квадратов (FGLS feasible generalized least squares)
8'SLS = (ІT (л-1 <g> Ig ) )-1 ZT (л-1 <g> Ig
известной под названием трехшаговой оценки наименьших квадратов, или SSLS-оценки (three-stage least squares).
2.6.4. Оценивание систем одновременных уравнений с использованием метода максимального правдоподобия
(
Запишем совокупность g одновременных уравнений для n наблюдений в виде: Y Г = X В + U ,
где
Y
матрица значений в n наблюдениях всех g
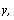 ng J
ng J
эндогенных переменных, включенных в систему,
x
11 x1K
X
матрица значений в n наблюдениях всех
V xn1
x
nK J
K предопределенных переменных, включенных в систему,
(.. ..
u11 K u1g
U
матрица значений в n наблюдениях
n1 ng J
случайных ошибок в g структурных уравнениях системы,
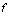
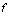
Г
В
матрицы
Yu ?ig 7g
Pk1 pKg J
Vі g1 Ygg J коэффициентов.
Сделаем следующие предположения относительно векторов ut =(ut1,K, utg) ошибок в g уравнениях в t -м наблюдении:
• векторы и1,к, un имеют одинаковое g -мерное нормальное
распределение Ng (0, Е) с нулевым вектором математических
ожиданий и положительно определенной ковариационной матрицей Е ;
• векторы и1,к, un независимы между собой.
При таких предположениях совместная плотность распределения случайных векторов щ,...,un имеет вид:
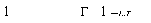 PU Un ) = П
PU Un ) = П
і ,—w , • expj —2utЕ~u>

 Ь(Г, В, Е| Г,X) = |detГ|n ■ І ((І2я)8т1 detЕ
Ь(Г, В, Е| Г,X) = |detГ|n ■ І ((І2я)8т1 detЕ
X expj — ^ X (yt Г — xt В)Е—1 (yt Г — xt В)т 1,
логарифм которой равен
ln L(r, Б, l| Y, X ) = n ln |det Г| n ln(det Z) ng ln(2n) ng
2І (У Г xt Б)І-1 (yt Г xt Б).
2 t =1
Продифференцировав последнее выражение по элементам матрицы Z-1 и приравнивая найденные производные нулю, приходим к соотношению:
Z = n _1(Y Г X b)(y Г X Б). Подставляя полученное выражение для Z в правую часть выражения для lnl(,Б,Z|Y,X) и отбрасывая слагаемые, не
зависящие от неизвестных параметров, получаем концентрированную логарифмическую функцию правдоподобия
lnL (Г, Б) = n ln|det Г --jln n(Y Г X Bf(Y Г X б).
Оценки матриц Г и Б находятся максимизацией ln L с учетом всех ограничений, накладываемых на коэффициенты структурных уравнений. В частности, если используются только исключающие и нормировочные ограничения, то максимизация проводится только по неспецифицированным элементам этих матриц. В процессе такой
максимизации матрица (Y Г X Б) (Y Г X В) должна иметь полный ранг для всех допустимых значений Г и Б . Необходимым условием для этого является условие n > g + K . Такое условие
может быть ограничительным для систем с большим количеством переменных.
Матрицы Г и IB , получаемые в результате максимизации ln L ,
и матрица X = n -1 (y Г X B)(y Г X B) вместе образуют оценку
максимального правдоподобия, учитывающую полную информацию о структуре модели одновременных уравнений. Поэтому такую оценку называют оценкой максимального правдоподобия с полной информацией (FIML full information maximum likelihood). Пусть
выполнены сделанные выше предположения,
ранговое условие идентифицируемости выполняется для всех структурных уравнений системы,
матрица X имеет полный ранг,
(1 T Л
предельная матрица p lim I — X X I = Q имеет конечные
элементы и положительно определена. Тогда FIML-оценка состоятельна и асимптотически нормальна. При этом требование нормальности распределения векторов u1, —, un не обязательно. (См., например, [Amemiya (1985), глава 7].)
З а м е ч а н и е 4
Если при выводе FIML отправляться не от структурной, а от приведенной формы системы, учитывающей ограничения, накладываемые на коэффициенты структурной формы, то тогда дело сводится к максимизации концентрированной функции правдоподобия
ln Г (Г, В) = 2in nl (y X ВГ1 J(y X ВГ1),
т.е., с учетом соотношения П = ВГ 1, к минимизации целевой функции
Q(r, В)=Q(n )=(Y X П J(Y X П) по элементам матрицы П с учетом ограничений, накладываемых на коэффициенты этой матрицы выбранной спецификацией матриц Г и В .
Если не учитывать эти ограничения при минимизации целевой функции Q(n), то при сверхидентифицируемости отдельных уравнений системы возникает неоднозначность восстановления Г и В по полученной оценке П . Если же все уравнения системы идентифицируемы точно, то значения Г и Б восстанавливаются однозначно и при этом восстановленные значения Г и В совпадают с оценками, полученными при минимизации <2(Г,Б) по Г и Б .
З а м е ч а н и е 5
При практической реализации метода FIML приходится использовать итерационные процедуры. Для обеспечения состоятельности и асимптотической нормальности FIML-оценки в качестве начальных значений параметров необходимо использовать их состоятельные оценки. Их можно получить двухшаговым методом наименьших квадратов. Если система неидентифицируема, то итерационный процесс может не сходиться.
З а м е ч а н и е 6
Перед применением FIML обычно производят исключение из системы тождеств и недоидентифицируемых уравнений.
З а м е ч а н и е 7
В рекурсивной системе с диагональной ковариационной матрицей Z оценка FIML получается применением OLS отдельно к каждому уравнению.
Пусть первое стохастическое структурное уравнение
у1 = Y1a1 + Xl61 + u1 идентифицируемо, а другие уравнения либо неидентифицируемы либо имеются сомнения в правильности их спецификации. Пусть при этом известен список всех предопределенных переменных, включаемых в систему, и значения этих предопределенных переменных в n наблюдениях, так что известна матрица X этих значений и можно говорить о приведенной форме системы:
Y = Xn + W .
Удалим из приведенной формы часть, относящуюся к у1; оставшаяся часть принимает вид:
Y = ХП1 + W1.
Вместо полной системы структурных уравнений или полной приведенной системы рассмотрим теперь смешанную систему:
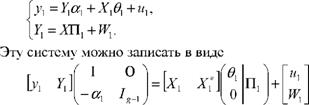
и применить к ней метод FIML. Такая процедура приводит к оценке параметров ос1,в1, П, называемой оценкой максимального правдоподобия с ограниченной информацией (LIML limited information maximum likelihood).
При практической реализации этой процедуры итерационными методами в качестве начальных значений следует использовать состоятельные оценки параметров <х1,в1, П1. Состоятельную оценку матрицы П1 можно получить непосредственным применением метода наименьших квадратов к уравнениям системы Y1 = ХП1 + W1. Состоятельные оценки параметров щ и в1 можно получить, применяя двухшаговый метод наименьших квадратов.
Обсуждение Эконометрика для начинающих (Дополнительные главы)
Комментарии, рецензии и отзывы
