2.3. некоторые распределения случайных величин

2.3. некоторые распределения случайных величин

Рассмотрим наиболее часто используемые в эконометрике распределения случайных величин.

Дискретная случайная величина X имеет биномиальный закон распределения, если она принимает значения О, 1, 2,..., aw,..., п с вероятностями

р(х = т) = C™pmqn-m, (2.15)

где 0 < р < 1, q = I — р, m = 0, 1,..., п.

Биномиальный закон распределения представляет собой закон распределения числа Х = т наступлений события А в п независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.

Формула (2.15) называется формулой Бернулли.

Числовые характеристики: М(Х) = пр, D(X) = npq.

В частности, для частости события W = — в п независимых

п

испытаниях (где X = т имеет биномиальный закон распределения с параметром р) числовые характеристики:

M(W) = р, D(W) =

п

Дискретная случайная величина X имеет закон распределения Пуассона, если она принимает значения 0,1, 2,..., т,... (бесконечное, но счетное множество значений) с вероятностями

/ ч Хте~х

р(Х = т) = -, (2.16)

ml

где т = 0, 1, 2,... .

Числовые характеристики: М(Х) = X, D(X) = X.

(2.17)

(baf

3. Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [а, Ь, если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.е.

—— при а<х<Ъ

при

х < а, х > Ь. а + Ь

D(X)

ф(*) =

Числовые характеристики: М(Х)

2 ' 4 ' 12 4. Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром X, если ее плотность вероятности имеет вид:

(2.18)

ф(*) = '

ГА.е_Ъг при х > 0;

0 при х < 0.

Числовые характеристики: М(Х)—, D(X) = ^-.

Х> Х1

5. Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами а и а2, если ее плотность вероятности имеет вид :

(x-af гє 2су2 .

(2.19)

ал/2я

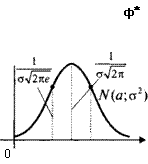
Кривую нормального закона распределения называют нормальной или гауссовой кривой (рис. 2.4). Числовые характеристики:

М(Х) = а, D(X)=o2.

При изменении только парамета-о а а+о х

ра а нормальная кривая перемещаРис2.4 ется вдоль оси Ох, при изменении

только параметра а2 меняется форма нормальной кривой.

Нормальный закон распределения с параметрами а = 0, а2 = 1, т.е. N(0;l)9 называется стандартным или нормированным.

Функция распределения случайной величины X, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле: ^ , ч 1 1 Jx-аЛ

Fn(x) = + -& , (2.20)

2 2 а )

2 х

где Ф(х)= —т=*е 2dt — функция (интеграл вероятностей) Лап-л/2я J0

ласа, равная площади под стандартной нормальной кривой 7V(0;1) на отрезке [—х9 х].

Свойства случайной величины, распределенной по нормальному закону:

Вероятность попадания случайной величины X, распределенной по нормальному закону, в интервал [х, xj], равна

р(хх < X < х2) = ± [Ф(*2) o(tx)], (2.21)

х а х2-а

где tx = , t2 = .

а а

Вероятность того, что отклонение случайной величины X, распределенной по нормальному закону, от математического ожидания а не превысит величину А > 0 (по абсолютной величине), равна

р(Х-а\< Л)=Ф(0, (2.22)

А

где t = — . а

Из второго свойства вытекает, в частности, правило трех сигм:

Если случайная величина X имеет нормальный закон распределения с параметрами а и а2, т.е. 7У(а;а2), то практически достоверно, что ее значения заключены в интервале (а За, а + За).

Непрерывная случайная величина X имеет логарифмически нормальное (сокращенно — логнормальное распределение), если ее логарифм подчинен нормальному закону.

Распределением у} (хи-квадрат) с к степенями свободы называется распределение суммы квадратов к независимых случайных величин, распределенных по стандартному нормальному закону, т.е.

Х2=І^,2, (2.23)

1 = 1

где Zt (і = 1, 2,..., к) имеет нормальное распределение N(0;1).

При к> 30 распределение случайной величины Z— ^2\%2 -yJ2kблизко к стандартному нормальному закону, т.е. N(0;1).

Распределением Стьюдента (или t-распределением) называется распределение случайной величины

(2.24,

lit*

где Z — случайная величина, распределенная по стандартному нормальному закону, т.е. N(0;l); у} — не зависимая от Zслучайная величина, имеющая х2-распределение с к степенями свободы.

При &-^+оо /-распределение приближается к нормальному. Практически уже при к>30 можно считать /-распределение приближенно нормальным.

Распределением Фишера—Снедекора (или F-распределением) называется распределение случайной величины

F = ^ , (2.25)

к2

где \%2(к1) и х2{к2) — случайные величины, имеющие х2-рас-пределение соответственно с к и к2 степенями свободы.