4.1.1. значение доходности и курс ценных бумаг при полной корреляции

4.1.1. значение доходности и курс ценных бумаг при полной корреляции

Сконцентрируйте внимание на первых трех ценных бумагах, показанных в табл. 4.1. Цена первого титула составляет р{Х) = 46 руб. Математическое ожидание возвратных потоков второй бумаги составляет Е(Х2) = 118 руб. Пусть доходности бумаг 1 и 2 имеют коэффициент корреляции +1 , а доходности акций 2 и 3 — коэффициент корреляции —1.

Начертите график, показывающий взаимосвязь между бумагами 1 и 2.

Определите математическое ожидание и дисперсию доходностей обеих ценных бумаг.

Какой курс должна иметь бумага 2?

Составьте уравнение для взаимосвязи между акцией 2 и акцией 3. Каковы величины математического ожидания и дисперсии доходности бумаги 3?

1. Если бумаги 1 и 2 имеют коэффициент корреляции +1, то между исходами доходностей в каждой возможной ситуации существует линейная взаимосвязь. Верно

r2s=a + brls при b>0 Vs. (4.1)

Доходность титула 1 будет рассчитана тогда, когда мы подставим зависимые от ситуации возвратные потоки в формулу

Ха p{Xi)

Гп =

P(*l)

Для первых двух ситуаций получаем

40 46 45 46

щ = = -0.1304 и г12 = = -0.0217.

46 46

Так как мы знаем соответствующие значения доходностей акции 2, мы можем подставить их в (4.1) и тогда получим

0.0630 = a + b(-0.1304), 0.1772 = a + b(-0.0217).

Эти формулы являются системой линейных уравнений с двумя неизвестными. Решение системы дает после округления а = 0.2 и b = = 1.05. При учете этих значений мы получим с помощью (4.1) для всех возможных ситуаций записанные в табл. 4.2 доходности титулов. Рис. 4.1, а показывает линейную зависимость между п и г2.

2. Математическое ожидание доходностей рассчитывается для S ситуации или с помощью

S

ЕИ = £'•.,<?.„ (4.2)

3=1

или (при знании ожидаемых возвратных потоков и цены) через

Если мы подставим соответствующие величины из табл. 4.2 в (4.2), то для ожидаемых доходностей получим

E[fi] = 0.3 • (-0.1304) 40.2 • (-0.0217) + 0.2 • 0.0870 40.3 • 0.3043 = = 0.0652.

Для того чтобы суметь оценить (4.3), нам необходимо математическое ожидание возвратных потоков. С данными из задачи мы получим

E[Xi] = 0.3 • 40 40.2 • 45 40.2 • 50 40.3 • 60 = = 49.

Из этого непосредственно следует

49 46

Е[п] = = 0.0652.

1 J 46

Дисперсия доходности ценной бумаги определяется как

S

Var[f] = J2(rs ~ E[r"])V (4.4)

.4=1

Подстановка дает

Var[fi] = 0.3 • (-0.1304 0.0652)2 40.2 • (-0.0217 0.0652)2 4-4-0.2 • (0.0870 0.0652)2 40.3 • (0.3043 0.0652)2 = = 0.0302.

Математическое ожидание и дисперсию доходности ценной бумаги 2 можно определить двумя разными способами. Сначала подстановка соответствующих данных из табл. 4.2 в (4.2) и (4.4) дает желаемые величины. Затем благодаря (4.1) верно

Щг2] = а + ЬЦгі],

E[f2] = 0.2 41.05 E[fi] = 0.2685

Var[f2] = b2V&r[rl},

Var[f2] = 1.052Var[fi] = 0.0334.

3. Цену p(X2) можно рассчитать с помощью

ЩХ2] Р(Х2)

Е[г2]

р(Х2

Если данную формулу выразить через р(Х2), то подстановка значений приведет к

4. При совершенно отрицательной корреляции взаимосвязь между обеими доходностями можно изобразить через прямую с отрицательным наклоном. Поэтому зависимые от ситуации доходности можно определить с помощью уравнения

?~3.s= а — fr7'2S, b > 0 Vs.

Подстановка соответствующих величин из первых двух строк табл. 4.1 приведет к получению системы линейных уравнений

0.2433 = а -Ь0.0630, 0.1405 = аЬ0.1772.

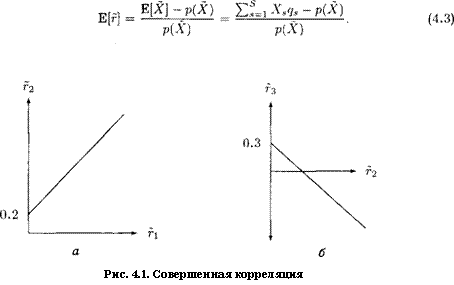
После решения этой системы мы получим изображенную на рис. 4.1, б линию

г3 = 0.3 0.9 г=2,

с помощью которой мы можем восполнить вектор доходности бумаги 3. Табл. 4.2 показывает результаты. В качестве математического ожидания и дисперсии получаем

Е[7"3] = 0.3 0.9Е[7~2] = 0.0584 Var[f3] = (-0.9)2 Var[r2] = 0.027. 4.1.2. Продажа без покрытия

Представьте себе, что на финансовом рынке существуют лишь две рисковые ценные бумаги 1 и 2 из табл. 4.1. Титулы в настоящее время обращаются по цене р{Х) = 46 и р{Х) = 93.03 руб. Вы ожидаете, что в t = 1 курсы будут составлять Е[Х\] = 49 и Е[Х2] = Н8 руб. Будучи не очень сильно нерасположенным к риску человеком, вы поставили себе цель вложить 11 000 руб. в высокодоходную, но также очень рисковую акцию 2. К сожалению, вы владеете лишь 10 000 руб., кроме того, не существует возможности получить кредит по безрисковой ставке процента. Что вы сделаете? Объясните свою стратегию. Какие издержки при этом вы должны нести, и какова ваша чистая прибыль?

* * *

Для того чтобы суметь осуществить инвестиции в объеме 11 000 руб. в акцию 2 без возможности получения кредита, существует «фокус», который называют продажей без покрытия. Вы можете получить отсутствующие средства таким образом: сначала вы найдете владельца ценных бумаг, который готов ссудить вам в t = 0 бумаги типа 1 стоимостью в размере 10 000 руб.,

если вы одновременно обязуетесь вернуть ему акции того же типа в том же количестве (1000/46 = 21.74) в момент времени t = 1. После этого вы продаете бумаги и вкладываете выручку в объеме 1000 руб. и свои собственные 10000 руб. в титул 2 ((11000/93.03 = 118.24 штук). Для того чтобы вы могли выполнить свое обязательство перед лицом, который ссудил вам акции, естественно, вам не остается ничего другого, как в момент времени / = 1 «обратно» купить необходимое количество этих акций по существующим в этот момент ценам. Если в момент времени t = 0 вы ожидаете, что эта цена будет составлять 49 руб., то ваши расходы на возвратную покупку составят 21.74 ■ 49 = 1065.22 руб. Ожидаемая выручка от продажи ценной бумаги 2 составит 118.24 • 118 = 13 952.49 руб. После осуществления всех сделок создается изображенная в табл. 4.3 картина. Ожидаемую чистую доходность в объеме 28.87\% мы получим и тогда, когда взвесим отдельные доходности по их доле и просуммируем полученные значения. Так как реализованный портфель на НО \% состоит из бумаги 2 и на —10 \% из бумаги 1, то для доходности мы можем записать

Е[г] = 1.1 • 0.2685 + (-0.1) • 0.0652 = 0.2887.

4.1.3. Кривая трансформации в случае с двумя ценными бумагами

Посмотрите на табл. 4.2 и сконцентрируйте внимание на ценной бумаге 2 и дополнительно на пятой обращающейся на рынке бумаге с математическим ожиданием Effe] = 0.15 и дисперсией Var[f5] = 0.01.

1. Составьте таблицу значений и покажите с помощью графика, какую структуру «доходность—риск» может выиграть тот, кто реализует портфель из этих двух бумаг. Исходите при этом из корреляции между доходностями обеих бумаг, равной д25 = -0.5.

Какую структуру имеет состоящий из обоих титулов портфель с наименьшим риском?

Определите комбинацию «доходность—риск», которой достигает инвестор, продающий без покрытия 50 \% бумаги 5 и инвестирующий выручку в титул 2.

* * *

При со, являющейся долей ценной бумаги 2, портфель из этих двух титулов достигает ожидаемой доходности величиной в:

Е[гР] = со 0.2685 + (1 ш) 0.15

и характеризуется риском

Var[rp] = J2 ■ 0.0334 + (1 to)2 ■ 0.01 -2 • 0.5-w(l-w)-0.1826-0.1. (4.5)

За счет вариации долей мы получим таблицу значений 4.4. Рис. 4.2 показывает кривую трансформации, похожую на гиперболу в осях «доходность—риск». С помощью такого портфеля невозможно совершенно уничтожить риск.

Портфель с минимальным риском, а значит, реализуемый портфель с наименьшим риском, создается путем дифференцирования (4.5) по

0.20-

Акция Г) (100 \%)

0.10

I 1 1 "І 1 1

0.05 0.10 0.15 0.20 0.25 0.30

агр

Рис. 4.2. Кривая трансформации

структурной переменной и) и приравнивания к нулю получаемого в ре-

л

зультате выражения1

dVar[rP}

2uj Var[f2] + 2(w 1) Var[/-5] + + Й5 2(1 2u>) <r[f2] = 0.

Если выразить данную формулу через uj, то подстановка даст-

Var[?>,] g-25 <7Ы (тїг>]

Var[r2] + Var[f5] 2 g2r, o[r2 о[їь

0.31.

1 Строго говоря, нужно было бы еще проверить и вторую производную для того, чтобы быть уверенным, что речь идет о минимуме. Мы не будем заниматься этим, не хотели бы обратить внимание читателей на то, что функция Var(oi) является параболой, поэтому условия второго порядка в любом случае оказываются выполненными.

Если инвестор хочет поддерживать риск на как можно более низком уровне, он должен инвестировать свое имущество на 31 \% в ценнук бумагу 2 и на 69\% в актив 5. 3. Если мы продаем титул 5 на 50 \% без покрытия, то посредством нашегс портфеля мы достигаем ожидаемой доходности

E[r>] = 1.5 • 0.2685 + (-0.5) • 0.15 = 0.3277.

Риск составляет

<т[гр] =v/l.5 • 0.0334 + (-0.5) • 0.01 + 2 • (-0.5) • 1.5 • (-0.5) • 0.1826 • 0.1 = = 0.302.

Рис. 4.2 показывает соответствующую структуру «доходность—риск».

4.1.4. Полная корреляция и кривая трансформации

Рассмотрите портфель, состоящий из бумаг 1 и 2, который показан в табл. 4.1. Определите кривую трансформации при условии, что продажи без покрытия запрещены.

Исходите из доходностей акций 2 и 3. Определите кривую трансформации и покажите, что с портфелем из титулов 2 и 3 можно совершенно уничтожить риск без осуществления продаж без покрытия. Как велика доля акций 2 в портфеле с минимальным риском?

*

1. Кривая трансформации является геометрическим местом всех комбинаций «доходность—риск», которых инвестор может достичь посредством «смешивания» двух ценных бумаг. Каждой точке кривой трансформации соответствует «своя» структура портфеля. Вид кривой зависит от корреляции между доходностями ценных бумаг. В этой задаче предполагается совершенно положительная корреляция между доходностями акций 1 и 2. Мы хотим показать, что кривая трансформации в этом специальном случае имеет вид прямой линии. Для этого нам необходима сначала формула доходности и дисперсии для портфеля, состоящего из акций 1 и 2. Для ожидаемой доходности Е[гр] верно

Е[гР] =wE[n] + (1 -ш)Е[г2] (4.6)

при и), являющейся стоимостной долей в портфеле акции 1. Дисперсия портфеля определена как

Var[fP] = J1 Var[ri] + (1 w) Var[r2] +

+2lj (1 ш) дм <т[г[] a[r2.

Для специального случая полной положительной корреляции (и только для этого случая) Var[r>] является возведенным во вторую степень

средневзвешенным стандартным отклонением'

2

Var[?V] = уи> о-[гі] + (1 w) ст[г2]

Если мы исключим возможность продажи без покрытия, ТО ДОЛЯ U) всегда находится в интервале [0,1]. Далее, так как не существует отрицательных стандартных отклонений, выражение в скобках в правой части должно быть положительным. Поэтому для стандартного отклонения мы получим

a[rp] =y/Var[fP] = u-' rrln] + (1 - а[Р2]. (4.7)

Если мы выразим формулу (4.G) через ш, то подстановка в (4.7) даст после преобразований

a[h E[f2] -a[f2 E[ri] , E[nj -r E[f-2]

o- i}-a[r2] o-[ri] a[r2]

Через подстановку цифр из табл. 4.2 можно рассчитать уравнение прямой линии

Щгр] = -3.9942 + 23.34 a[rrl

Прямая линия в области 0.1739 < а[гР] < 0.1826 соответствует искомой кривой трансформации при полной положительной корреляции, если продажа без покрытия не допущена (см. рис. 4.3).4

На самой северной точке портфель состоит на 100 \% из ценной бумаги 2. На южном конце все имущество вложено в ценную бумагу 1. Точка Q отражает комбинацию «доходность—риск» для портфеля, которая состоит на 80\% из бумаги 1 и на 20\% из бумаги 2. Координаты Q мы получаем через

E[rQ] = 0.8 E[n] + 0.2Е[7'2] = 0.1059

и

a[rQ] = 0.8 a[ri] + 0.2 a[r2] = 0.1757.

Это можно легко увидеть, если мы вспомним биномиальную формулу. Если мы приравняем а = ы о[г\] и b = (1 — ш) о[г2], то дисперсию можно определить как

Var [гр] = (а + Ь)2 = а2 + Ь2 + 2аЬ.

4 При дисперсии, равной Var[r2] = 0.0334, которую мы определили на с. 146, получаем стандартное отклонение y/Var[r2] = 0.1826.

Уничтожить риск при исключении продаж без покрытия невозможно, так как все достижимые позиции «доходность—риск» можно изобразить лишь как положительные линейные комбинации позиций «доходность—риск» обеих ценных бумаг.

Е[гр]

1 и

0.25 

0.05

0.0т

0.81.0і

ТІ.0

-0.2

-4J.0

a[rp

0.16

0.17

0.18

0.19

Рис. 4.3. Кривая трансформации с д =

2. Доходности акций 2 и 3 имеют коэффициент корреляции —1. Для того чтобы показать, что риск можно уничтожить полностью, мы используем две формулы

(4.8)

и

Но для выведения кривой трансформации мы сейчас предложим другой способ, отличающийся от способа, содержащегося в задаче 4.1.4, 1. Выражение в скобках, которое мы должны возвести во вторую степень, может стать как положительным, так и отрицательным. Но так как не существует отрицательных стандартных отклонений, их нужно исключить. Для этой цели мы в скобках учтем различие случаев и скомбинируем их со знаком перед скобкой таким образом, что результат в любом случае не станет отрицательным

(4.9)

Вначале мы определим для обоих случаев наклон кривой трансформации и после этого используем обе координаты (£[fo], СТ^]) и (Е[гз], ст[гз]). Оказывается, что кривая трансформации сложена из двух прямых линий.

Случай 1. Знак выражения в скобках в (4.9) является положительным

а[гр] = to a[i'2} о[гз].

(4.10)

Мы дифференцируем сначала (4.8) и (4.10) по ш и определяем после этого при учете

= E[f2] E[f3]

О Щгр] _ дЩг1>}/ди 0(т[гр] да[гр/дш наклон кривой трансформации. При

дЕ[гР] Эй)

р

и

= СГ7-2 +^ ГЗ

У erfV

мы получим после подстановки значений из табл. 4.2

ЭЕ[гр] E[f2] Е[г3]

т;—f—т = гі F^T = 0.0055.

9(7[гр| о[г2 + 0-[Г'і

Так как наклон постоянен, то кривая трансформации в случае 1 имеет вид прямой с положительным наклоном в форме Е[гР] = а+ 0.6055 а[гР]. Случай 2. Знак выражения в скобках в (4.9) отрицателен. Наклон кривой трансформации определяется аналогично случаю 1. Он составляет

ЭЕ[гр] = Е[г2]-ЕЫ = _о б()55 да[гр] -о[г2 <т[г3]

Мы получаем прямую линию вида Е[гР] — а — 0.6055 о-[г>]. Кривая возможных действий, очевидно, образуется из двух прямых линий по абсолютной сумме одинакового наклона. Нам известны две координаты кривой. Они могут находиться на одной и той же прямой линии лишь при полной положительной корреляции, см. с. 152. При имеющемся здесь коэффициенте корреляции -1 мы можем исключить возможность того, что точки (Е[г"г], crfj^]) и (Е[г"з], о-[г3]) лежат на одном и том же отрезке прямой. Кроме того, так как продажи без покрытия не допущены, мы знаем, что обе координаты являются самыми восточными точками кривой трансформации в координатах «доходность— риск». Поэтому северная точка должна находиться на отрезке кривой трансформации с положительным наклоном, южная — на отрезке с отрицательным наклоном. После этих предварительных рассуждений мы можем по отрезкам определить кривую трансформации через подстановку соответствующих координат в общую формулу уравнения у = = а + Ьх. При

0.2685 = а + 0.6055 ■ 0.1826

и

0.0584 = а 0.6055 • 0.1644 для северного отрезка получим

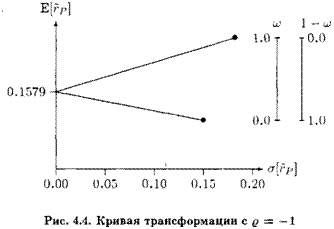
Щгр] = 0.1579 + 0.6055 а[гР]

и для южного

Е[гР] = 0.1579 0.6055 а[гР].

Рис. 4.4 показывает комбинацию «доходность—риск», которая достижима при разных структурах портфеля. В общем отрезке ординаты обоих прямых при положительной ожидаемой доходности дано совершенное уничтожение риска. Здесь находится также портфель с наименьшей дисперсией. Для специального случая д2з = —1 портфель с наименьшим риском приносит гарантированную (безрисковую) доходность. Структуру можно рассчитать, если приравнять к нулю (4.9) и выразить эту формулу через структурную переменную''

<г[гз]

из = —.—г1——.—г = 0.4737. а[т2] + а[гя]

Портфель с наименьшим риском содержит на 47.37\% ценную бумагу 2 и на 52.63 \% ценную бумагу 3. Он приносит в каждой ситуации s одинаковую доходность

гРя = 0.4737 г2я + 0.5263 г3., = 0.1579.

4.1.5. Кривая трансформации при трех ценных бумагах

Пусть рынок капитала состоит из трех рисковых ценных бумаг.

0 Альтернативно к этому мы получаем также из, если мы подставим значение отрезка ординаты в формулу (4.8).

Ценные бумаги	А	в	С
	0.10	0.15	0.20
Varjf]	0.01	0.0625	0.16

Коэффициенты корреляции в связи с доходностями ценных бумаг составляют

QAD = -0.5, QAC = 0, две = -0.6.

Рассчитайте портфели из двух ценных бумаг, имеющие структуру с наименьшей дисперсией.

Каковы доходность и риск портфеля, который состоит из одинаковых долей трех ценных бумаг?

Оцените кривую трансформации для портфеля из трех ценных бумаг.

* *

1. Структура портфеля с наименьшим риском при двух ценных бумагах рассчитывается по формуле

_ Var[7~2] Cov[ri, 7~2]

Var[n] + Var[f2] 2 Cov^i, 7~2]'

причем uj является долей первой бумаги. При учете

Cov[fi,f"2] = Qv2o[rx]e[r2

мы получаем для портфеля, состоящего из бумаг А и В,

- 0.0625(-0.5)0.1-0.25 U)A~ 0.01 + 0.0625 2(-0.5) 0.1 -0.25 ~ '? ' и)В = 1-и)А= 0.2308,

для портфеля, содержащего А и С,

0.16 0 • 0.1 • 0.4 Шл = 0.01 + 0.16-2.0.0.1.0.4 = °'9412' и>с = 1 ша = 0.0588

и для портфеля, в котором содержатся акции В и С,

_ 0.16(-0.6)0.25.0.4 _ ШВ ~ 0.0625 + 0.16 2 (-0.6) 0.25 • 0.4 ~ °' 42 ' и>с = 1 — wb = 0.3577.

Табл. 4.5 показывает координаты соответствующих портфелей с наименьшей дисперсией.

2. Дисперсию портфеля, в котором содержатся одинаковые доли бумаг А, В и С, мы рассчитаем с помощью формулы

Доходностью портфеля является средневзвешенное значение отдельных доходностей

Е[Гр] = I 0.1 + ^ 0.15 + ]0.20 = 0.15.

О О о

3. При трех ценных бумагах возможные портфели находятся уже не на одной кривой, а на плоскости в виде формы яичной скорлупы. Вид этой плоскости представлен на рис. 4.5 для трех бумаг А, В и С.

ь При этом мы должны уяснить для себя, что Cov[ri,fi] = Var[fi]. Для этого способа расчета сравни: Copeland Т. Е., Weston J. F. Financial Theory and Corporate Policy. 3rd ed. Reading (Mass.): Addison-Wesley, 1988. P. 175.

1 *а[гр]

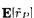Рис. 4.5. Кривая трансформации при трех ценных бумагах

Если мы предположим, что продажа без покрытия недопустима, то краем плоскости окажется оболочка кривой трансформации для соответствующих портфелей из двух ценных бумаг. Позиция D отражает портфель с абсолютно минимальной дисперсией.

4,1.6. Линия эффективности

На рынке обращается много ценных бумаг. Объясните, почему линия эффективности состоит лишь из северной ветви кривой трансформации. Исходите из того, что риск ценной бумаги с более низкой доходностью меньше, чем риск титула с самой большой доходностью.

*

*

*

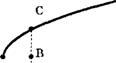
Линия эффективности — это геометрическое место всех доминирующих позиций «доходность—риск». О доминирующих позициях мы говорим тогда, когда невозможно достичь через альтернативную смесь портфеля более высокой доходности при том же риске. Как показывает рис. 4.6, это свойство имеют лишь позиции, которые находятся на северном крае кривой трансформации. Точка С является одной такой доминирующей смесью ценных бумаг. Напротив, портфели А и В, которые имеют одинаковый риск и поэтому лежат на вертикальной линии С, являются неэффективными.

Е[г]

А

1 . . . а[г]

Рис. 4.6. Кривая эффективности 4.1.7. Кривая эффективности для экономики в целом

Обоснуйте, почему кривая эффективности для экономики в целом должна иметь положительный наклон и быть строго выпуклой вверх.

* * *

На рис. 4.7 слева изображена кривая эффективности с (гипотетической) снижающейся ветвью. Рассмотрим комбинацию «доходность—риск» Q. Ни один не расположенный к риску инвестор не стремился бы к позиции Q, так как он мог бы достичь той же самой доходности E[?V]q и с меньшим риском asQ не эффективна, как и все позиции на снижающейся ветви. Следовательно, кривая эффективности имеет во всей области определения положительный наклон. Для обоснования строгой выпуклости вверх кривой эффективности проверим, может ли она быть выпуклой вниз или линейной. Если нам удастся исключить эти два вида прохождения, то должна иметь место выпуклость вверх.

Давайте сначала исследуем возможность выпуклой вниз кривой эффективности. Эта возможность изображена в правой части рис. 4.7. Здесь мы можем составить портфели из позиций L и N. Как мы знаем из теории портфеля, эти позиции в наихудшем случае имеют коэффициент корреляции + 1. Тогда все смеси можно изобразить в виде линейной комбинации N и L. Почему здесь речь идет о наихудшем случае, мы можем себе легко уяснить, если исходя из N составим смесь из обеих позиций. Рост доходности ДЕ [г],

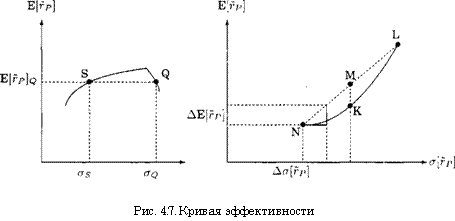которого можно достичь за дополнительную единицу риска Дст[г], является постоянным и всегда меньшим, чем при корреляции д < +1. Проверим все-таки один раз эту структуру и рассмотрим М. Портфель М по сравнению с портфелем К является доминирующим, так как он имеет при том же риске более высокую доходность. Как К, так и все другие точки на (гипотетической) выпуклой вниз кривой, являются субдоминантными по сравнению с портфелями на прямой линии. Поэтому кривая эффективности не может иметь выпуклые вниз участки.

Сейчас давайте проверим еще возможность того, что прямая линия окажется линией эффективности. Такой вид графика хотя и является теоретически возможным, но возникает лишь тогда, когда обращающиеся на рынке капитала ценные бумаги совершенно положительно коррелируют и все комбинации доходности и риска с минимальной дисперсией находятся на одной и той же прямой линии соединения. Это предполагает, что портфели можно создать всегда лишь из двух ценных бумаг. Очевидно, такой вывод явно противоречит действительности. Следовательно, единственно возможной формой линии эффективности остается ее строгая выпуклость вверх.

4.1.8. Выбор портфеля при одном рисковом финансовом титуле

Инвестор имеет функцию полезности

и(Цг], o[r) =a + b Е[г] + с Е[г]2 + с а{г}2.

Рассчитайте предельную норму замещения в общем виде и для конкретных значений b = 0.2 и с = -0.825082.

Какие комбинации «доходность—риск» достижимы для инвестора, если можно инвестировать лишь в две ценные бумаги:

ценную бумагу 4 из табл. 4.1 и

ценную бумагу 6 с математическим ожиданием Е[га] = 0.1 и стандартным отклонением ст[г«] = 0.08?

Цена для бумаги 4 составляет 50 руб. Продажи без покрытия допущены.

Определите оптимальный портфель.

Является ли инвестор заемщиком или кредитором?

* * *

Предельную норму замещения можно определить, приравняв к нулю полный дифференциал функции полезности

dU = (b + 2cE{P]j • dE[r] +2сст[г] • da[f] =0 и выразив его через

,„т,„ dEfrl 2 ест Ь-]

MRS = —4гт = -т—п J,,. da{f] b + 2cE[r]

Мы сейчас подставим конкретные значения в MRS и получим

2-(-0.825082) ст[г] MRS" "0.2 + 2. (-0.825082) Е[г]' (4Л1)

Цена бумаги 4 является безрисковым вложением с доходностью, равной

52.5 50

П = = 0.05.

50

Кривую трансформации портфеля с безрисковыми и рисковыми активами можно определить при учете стандартного отклонения

ст[г] = s/uj2 Var[7-Gj + (1 ш)2 Var[7-4j + 2 cj (1 uj) Cov[f4,

дисперсии Var[r4] = 0 и ковариации Cov[f4,ft;] = 0 — с помощью уравнения доходности портфеля

E[i']=wE[rfi] + (l-w)f4 =

= w(E[7-c]-f4)+r4 (4.12)

Так как мы допустили продажу без покрытия, то каждый инвестор может первым делом получить кредит по ставке процента г~4 (ш > 1) или вторым делом продать рисковый актив 6 без покрытия (ш < 0). Поэтому мы можем переписать стандартное отклонение как

a ] = ± ш(тг6].

Если выразить данную формулу через uj, то подстановка в (4.12) даст

Е^с] г і ...

Е г = г., ± —— а г .

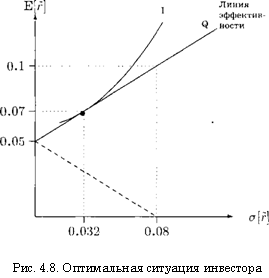Линия трансформации состоит из отрезков прямой с безрисковой ставкой процента, соответствующей оси ординаты (рис. 4.8). Все точки,

достижимые за счет продажи без покрытия бумаги б, находятся на пунктирной линии

Прямая линия пересекает ось абсцисс при а[г] = 0.08, что мы можем легко проверить за счет приравнивания к нулю предыдущего уравнения. Для определения структуры принадлежащего портфеля мы приравниваем (4.12) к нулю и выражаем через структурную переменную с результатом и = —1. Инвесторы считаются лишь с продажей без покрытия титула 4, так как продажа без покрытия акции 6 приведет к неэффективным комбинациям «доходность—риск». Кривая эффективности характеризуется уравнением

0.1 0.05

Е ?■ = 0.05 + аг] = 0.05 + 0.625а г].

1 J 0.08 11 1 i

3. MRT (предельная норма трансформации) соответствует наклону линии эффективности. При учете (4.11) условие оптимального портфеля выглядит следующим образом:

2 (-0.825082) а[г)

0.625. (4.13)

0.2 + 2 (-0.825082) Е[г] Путем подстановки

Е[г] = w0.1 + (1-cj) 0.05 = 0.05 + а;0.05 (4.14)

и

0.625.

а[г] = и;а{г6] = и 0.08 (4.15) в (4.13) получим уравнение определения

2 (-0.825082) 0.08 и;

0.2 + 2 (-0.825082) (0.05 + ш 0.05)

Если выразить данную формулу через л, то это приведет к структуре портфеля, максимизирующего полезность:

uj = 0.4 (доля рисковой ценной бумаги 6) и

1 — lj = 0.6 (доля безрискового актива 4).

Подстановка ш в (4.14) и (4.15) приведет к точкам, отражающим выбранный портфель,

сг[г] = 0.4 • 0.08 = 0.032

и

Е[г] = 0.05 + 0.4 ■ 0.05 = 0.07.

Оптимальная ситуация инвестора изображена на рис. 4.8. 4. Безрисковая ценная бумага содержится в портфеле с долей 1 и > 0. Поэтому инвестор является кредитором. В оптимуме он ссужает 60 \% своего имущества. Положение заемщика в точке Q (рис. 4.8) требует продажи без покрытия титула 4 и, таким образом, 1 — о.' < 0.

4.1.9. Отношение к риску и выбор портфеля

Ваши предпочтения характеризуются слабой нерасположенностью к риску, и при этом вы хотите оптимизировать свой портфель. На рынке капитала обращается много ценных бумаг. Ваш друг рекомендует вам купить портфель с наименьшим риском. Последуете ли вы совету вашего друга?

* * *

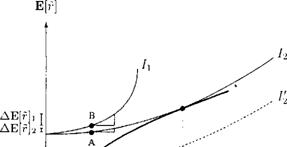
Кривые безразличия инвесторов, характеризующихся слабой нерасположенностью к риску, являются относительно пологими, а тех, кто сильно не расположен к риску, — относительно крутыми. Данный тезис проиллюстрирован на рис. 4.9.

Аа[г] сг[г]о,л Рис. 4.9. Виды отношения инвесторов к риску

Пусть її будет кривой безразличия инвестора i, а 1-і — инвестора г2. Рассмотрим положение с одинаковым риском А и В. Исходя из В инвестор ?'i готов принять на себя одну дополнительную единицу риска Аа[г] лишь тогда, когда это компенсируется относительно высокой доходностью ДЕ[г]|. Требование высокой компенсации отражает его сильную нерасположенность к риску. Инвестору І2 нужно компенсировать для принятия дополнительного риска лишь относительно низкую дополнительную доходность ДЕ[г]2, и поэтому его нерасположенность к риску можно охарактеризовать как слабую.

Безразличные к риску инвесторы по этим соображениям имеют горизонтальные кривые безразличия. Эта категория инвесторов не требует компенсации для принятия на себя дополнительного риска. Вертикальные кривые безразличия указывают на то, что инвестор готов к дополнительному принятию на себя риска лишь в том случае, если он будет вознагражден бесконечно большой дополнительной доходностью. Такой инвестор является «бесконечно» не расположенным к риску.

Оптимальный портфель находится в точке касания кривой трансформации и кривой безразличия. Здесь верен тезис: «Предельная норма трансформации (MRT) равна предельной норме замещения (MRS)». Так как кривая трансформации при характеризующей портфель с минимальным риском комбинации «доходность—риск» имеет бесконечный наклон, этот портфель мог бы быть лишь тогда вашим оптимальным портфелем, когда вы бы-. .it «бесконечно» не расположены к риску. Но это противоречит данной задаче, где ваша нерасположенность к риску была охарактеризована как слабая. Ваш оптимальный портфель должен находиться в пологой области линии эффективности при относительно высоких значениях комбинации «доходность—риск». Вы никогда не стали бы держать портфель D с минимальным риском из-за связанной с этим потери полезности (і2 >12) 

Литература

Теория портфеля основывается на работе: Markowltz Н. М. Portfolio Selection. Efficient Diversification of Investments. New York: Wiley, 1959. Одними из самых лучших вторичных источников можно считать: Copeland Т. Е., Weston J. F. Financial Theory and Corporate Policy. 3rd ed. Reading (Mass.): Addison-Wesley, 1988 и: Elton E. J., Gruber M. J. Modern Portfolio Theory and Investment Analysis. 5th ed. New York: Wiley, 1995. Тем читателям, которые особенно интересуются практическим применением теории, рекомендуется также Ross S. A., Westerfield R. W., Jaffe J. F. Corporate Finance. 3rd ed. Homewood (111.): Irwin, 1993.