2.4. многомерные случайные величины. условные законы распределения

2.4. многомерные случайные величины. условные законы распределения

Упорядоченный набор Х=(Х9 Х2,..., Хп) случайных величин называется многомерной (n-мерной) случайной величиной (или системой случайных величин^ n-мерным вектором).

Например, погода в данном месте в определенное время суток может быть охарактеризована многомерной случайной величиной Х=(Х9 Х2,..., Хп)9 где Х — температура, Х2 — влажность, A3 — давление, Х4 — скорость ветра и т.п.

Функцией распределения п-мерной случайной величины (Х9 Х2,..., Хп) называется функция F(x, х2,...,хп), выражающая вероятность СОВМеСТНОГО ВЫПОЛНеНИЯ п Неравенств Х\<х9 Х2<Х2,...,

Хп<хп, т.е.

F{xuxl9...9 хп) = Р(Х{ <xl9X2<x29...9 Хп <хп). (2.26)

В двумерном случае1 для случайной величины (X,Y) функция распределения f(x, у) определится равенством:

f{x,y) = P(X<x, Y<y). (2.27)

Свойства функции распределения f(x, у), аналогичные свойствам одномерной случайной величины:

0<F(x,.y)<l;

прих2>*і F(x2,y)> F(xi,y); приу2>У f(x, у2) > f(x, уг);

f{x, оо) = F(оо, у) = f{оо-оо) = 0;

4) F(x, + oo)=F,(4 F(+*o,y) = F2(y)9 где F{(x) и F2(y) функции распределения случайных величин X и Y;

5) F(+oo,+oo)=l.

Плотностью вероятности (плотностью распределения или совместной плотностью) непрерывной двумерной случайной величины (X,Y) называется вторая смешанная частная производная ее функции распределения, т.е.

ф у) = д2р(х'у) = F"xy(x, у} (2.28) дхду

Свойства плотности вероятности двумерной случайной величины ф(х, у) аналогичны свойствам плотности вероятности одномерной случайной величины:

Ф(х, у) > 0;

Р[(Х, Y)eD]=jjq>{x,y)dxdy;

D

f(x,y)= y(x,y)dxdy;

J-00 J—00

p+00 p+OO

4) <p(x9y)dxdy = l.

J—CO J-00

Условным законом распределения одной из одномерных составляющих двумерной случайной величины (X, Y) называется ее закон распределения, вычисленный при условии, что другая составляющая приняла определенное значение (или попала в какой-то интервал).

Условные плотности вероятности <ру(х) и (рх(у) двумерной

1 В дальнейшем для простоты изложение ведем в основном для двумерной (я=2) случайной величины, при этом практически все понятия и утверждения могут быть перенесены на случай п>2.

случайной величины (X, Y) определяются по формулам:

ф(*>7)

» ФхО0 =

ФіОО

(2.29)

или

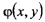<f(x,y)

; ф,О0 =

J—оо

J—00

Условные плотности ф^(х) и фх0>) обладают всеми свойствами «безусловной» плотности, рассмотренной в §2.2.

Числовые характеристики условных распределений: условные математические ожидания Мх( У) и Му(Х) и условные дисперсии DX(Y) и Dy(X). Эти характеристики находятся по обычным формулам математического ожидания и дисперсии, в которых вместо вероятностей событий или плотностей вероятности используются условные вероятности или условные плотности вероятности.

Условное математическое ожидание случайной величины У при Х=х, т. е. Мх( У), есть функция от х, называемая функцией регрессии или просто регрессией У по Х аналогично Му(Х) называется функцией регрессии или просто регрессией X по У. Графики этих функций называются соответственно линиями регрессии (или кривыми регрессии) У по Хи Хпо У.

Свойства условного математического ожидания:

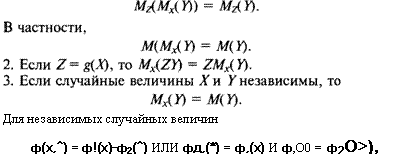где Фі(лО,ф2(>0 — плотности соответствующих одномерных распределений случайных величин Хи Y; <ру(х)9<рх(у) — плотности

их условных распределений Хпо У и У по X.

Зависимость между двумя случайными величинами называется вероятностной (стохастической или статистической), если каждому значению одной из них соответствует определенное (условное) распределение другой.

Например, зависимость между урожайностью и количеством внесенных удобрений — вероятностная.

Ковариацией (или корреляционным моментом) Со(Х, У) случайных величин X и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е.

соу(х, Y) = М[(Х ах )(Y -ау)]9 (2.30)

где ах = М(Х), ау = M(Y).

(Для ковариации случайных величин X и Y используются также обозначения К^, а^.)

Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и их рассеяние вокруг точки (ах, ау). Ковариация — величина размерная, что затрудняет ее использование для оценки степени зависимости случайных величин. Этих недостатков лишен коэффициент корреляции.

Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратиче-ских отклонений этих величин:

Cov(X,Y)

р = . (2.31)

охоу

Из определения следует, что коэффициент корреляции — величина безразмерная — характеризует тесноту линейной зависимости между случайными величинами.

Свойства ковариации двух случайных величин:

Со(Х, Y) = 0, если Хи Y независимы;

Cow(X, Y) = М(Х, Y) ауау;

|Cov(JT, Y) <ajpy.

Свойства коэффициента корреляции:

-1<Р< 1;

р = 0, если случайные величины Хи 7независимы;

если I р I =1, то между случайными величинами X и Y существует линейная функциональная зависимость.

Из независимости двух случайных величин следует их некоррелированность, т.е. равенство р = 0. Однако некоррелированность двух случайных величин еще не означает их независимость.

2.5. Двумерный (/т-мерный) нормальный закон распределения

Случайная величина {случайный вектор) (X, Y) называется распределенной по двумерному нормальному закону, если ее совместная плотность имеет вид:

Ф* (*, у) = Ц=—<г*М (2.32)

2пихиуЛ]і-р2

где

L{x,y)-2(1-P2)

Г Л2

x-aY

2

V °У J

(2.33)

= rv2

Числовые характеристики: А/(Л) = ах, M(Y) = ау, D(X) = ах, D(Y) = vj, Рху=р.

При этом одномерные случайные величины Хи Yраспределены нормально с параметрами соответственно (аХ9<зх (а 9а*).

(2.34) (2.35) (2.36) (2.37)

Условные законы распределения X по Y и Y по X — также нормальные с числовыми характеристиками:

Му(х) = ах+р^-(у-ау)9

Dy{x) = a2x(l-p2);

Mx(Y)=ay+p^-(x-ax

Dx(r) = a5(l-p2).

Из формул (2.34), (2.36) следует, что линии регрессии Му (X) и Л/д(Y) нормально распределенных случайных величин представляют собой прямые линии, т. е. нормальные регрессии Y по X и X по Y всегда линейны.

Для нормально распределенных случайных величин термины «некоррелированность» и «независимость» равносильны.

Понятие двумерного (п = 2) нормального закона обобщается для любого натурального п.

Нормальный закон распределения п-мерной случайной величины (n-мерного случайного вектора) Х= (Х9 Л^,.-» \%п) характеризуется параметрами, задаваемыми вектором средних а = (а902,...,а^' и ковариационной матрицей ]Г х = К )пхп, где а у = M[(Xt at )(Xj а})].

Ковариационная матрица и ее определитель, называемый обобщенной дисперсией n-мерной случайной величины, являются аналогами дисперсии одномерной случайной величины и характеризуют степень случайного разброса отдельно по каждой составляющей и в целом по я-мерной величине.