3.2. перечисление путей на графе

3.2. перечисление путей на графе

При решении отдельных задач теории графов возникает необходимость строить пути — все или только некоторые, — соединяющие две заданные вершины графа. Очевидно, что для связных графов всегда существует хотя бы один такой путь. Построение всех путей данного вида называется перечислением путей и представляет собой, по существу, полный последовательный перебор всех возможных вариантов путей, соединяющих заданные вершины. Рассмотрим соответствующий алгоритм перечисления путей.

Для реализации алгоритма все вершины графа упорядочиваются каким-либо образом (по номерам, по алфавиту или иначе). В упорядоченном наборе вершин графа каждая вершина имеет свой единственным образом определенный порядковый номер, который мы будем обозначать символом «#». Например, если все вершины графа снабжены индексами от 1 до п, то естественно упорядочить их по возрастанию индексов; при этом

#«i = l, #V2 = 2,...,#Vn = n.

Две заданные соединяемые начальную и конечную вершины будем обозначать «нач и vKOH. На каждом шаге алгоритма фиксируются два объекта:

некоторый построенный текущий путь

«нач = «[0] — Щ — • • • — V[k]

из начальной вершины г>нач в текущую вершину ьщ графа (отметим еще раз, что для вершины ее порядковый номер і в текущем пути может не совпадать с ее порядковым номером # «[j] во множестве вершин графа);

индекс р, определяющий минимальный номер подлежащих рассмотрению вершин на данном шаге.

На начальном шаге алгоритма (и некоторых последующих шагах) фиксируется «пустой» путь, не содержащий ребер и сводящийся к единственной вершине г>нач — ьщ.

При работе алгоритма перечисления путей с целью достижения конечной вершины применяются две следующие основные операции: удлинение и укорачивание текущего пути.

Удлинение. Для удлинения текущего пути просматриваются по порядку все вершины графа, смежные с крайней вершиной ущ текущего пути и не входящие в уже построенный путь (чтобы избежать повторения вершин). Просмотр начинается с номера р (это позволит избежать «зацикливания» в работе алгоритма). Если при просмотре найдена хотя бы одна вершина, то удлинение является возможным. Первая по порядку из найденных вершин (чтобы не допустить пропуска возможных вариантов удлинения) принимается искомым продолжением текущего пути и обозначается через V[k+1y Текущий путь становится на 1 ребро длиннее и принимает вид

Индекс р полагается равным 1, параметр к увеличивается на 1. Если же при просмотре не найдено ни одной подходящей вершины, то удлинение является невозможным.

Укорачивание. Если число к ребер в текущем пути больше 0, то укорачивание является возможным. Конечная вершина ущ текущего пути отбрасывается, и его новой конечной вершиной становится У[к_ц. Текущий путь становится на 1 ребро короче и принимает вид

ь[о]-Щ~~ ■■■ — «[к-і]Индекс р полагается равным # + параметр к уменьшается на 1. Если же число ребер в текущем пути равно 0, т. е. путь не содержит ребер вообще и сводится к одной вершине г>[0] = г>нач, то укорачивание является невозможным.

Например, если на графе, изображенном на рис. 3.2, фиксирован текущий путь V4 — V2, то операция удлинения при р — 4 приведет к следующему: вершины V,V2,v^ пропускаются, поскольку имеют номера, меньшие р; вершина V4 игнорируется, поскольку уже входит в текущий путь; вершина v5 позволяет осуществить требуемое удлинение и построить новый путь

Щ — V2~V5.

После укорачивания этого пути получим исходный путь V4 — V2, однако индекс р станет равным (#и5+1) = 6. Дальнейшее удлинение этого пути невозможно, поскольку единственная допустимая по номеру вершина г>6 не является смежной с конечной вершиной г>2 пути.

Алгоритм перечисления путей включает следующие пункты (шаги). (Как обычно, мы принимаем, что все пункты алгоритма выполняются в порядке возрастания их номеров, если иное не оговорено явно и не указан другой подлежащий выполнению пункт.)

Начало работы алгоритма. Построение путей начинается, естественно, с начальной вершины. Полагаем

V[o] = г>нач, Р = 1, k = 0; в данный момент текущий путь является «пустым».

Проверка. Если конечная вершина ущ текущего пути совпадает с конечной вершиной vKOH, т. е. ущ = «кон, то очередной из путей, соединяющих 1>Нач и vKOH, построен. Запоминаем построенный путь и переходим к п. 4 к укорачиванию текущего пути. Если же

^ fKOH, то переходим к п. 3 к удлинению пути.

Удлинение. Если операция удлинения возможна, то проводим ее и переходим к п. 2. Если же удлинение невозможно, то переходим к п. 4.

Укорачивание. Если операция укорачивания возможна, то проводим ее и переходим к п. 3. Если же укорачивание невозможно (это означает, что все пути уже построены), то переходим к п. 5.

Конец работы алгоритма.

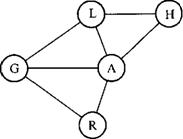
Применим рассмотренный общий алгоритм для построения всех путей, соединяющих вершину G с вершиной Н в графе, представленном на рис. 3.3. В рассматриваемом примере вершины графа удобно упорядочить в соответствии с их обозначениями по латинскому алфавиту; при этом

#А = 1, #G = 2, #Н = 3, #L = 4, #R = 5. Выполним подробно несколько первых шагов алгоритма перечисления путей.

— Полагаем ьщ — G, р = 1, к = 0.

Поскольку вершина G не совпадает с конечной вершиной Н то переходим к п. 3 алгоритма (далее будем говорить коротко «переход к п. 3»).

Для вершины G смежными являются вершины A, L, R, причем ни одна из них к текущему пути не относится. Поскольку р = 1 то минимальный допустимый номер 1 имеет вершина А, которая и является искомым продолжением. Текущий путь принимает вид G —А, индекс р полагается равным 1, параметр & —равным 1. Переход к п. 2.

Поскольку вершина А не совпадает с конечной вершиной Н, то переходим к п. 3.

Для конечной вершины А текущего пути смежными являются все остальные вершины графа, причем к текущему пути не относятся Н, L, R. Поскольку р = 1, то минимальный допустимый номер имеет вершина Н, которая и является искомым продолжением. Текущий путь принимает вид G А — Н, индекс р полагается равным 1, параметр & —равным 2. Переход к п. 2.

Вершина Н является конечной вершиной. Запоминаем построенный путь. Переход к п. 4.

Укорачивание является возможным. Вершина Н текущего пути отбрасывается. Текущий путь принимает вид G — А, индекс р полагается равным #Н + 1 = 4, параметр & —равным 1. Переход к п. 3.

Для вершины А смежными вершинами, не относящимися к текущему пути, по прежнему являются вершины Н, L, R. Однако в настоящий момент (в отличие от рассмотренной выше ситуации) р — 4. Поскольку # Н = 3, # L = 4, то теперь допустимым продолжением является вершина L. Текущий путь принимает вид G — А — L, индекс р полагается равным 1, параметр к — равным 2. Переход к п. 2 и т. д. по алгоритму.

Результаты проведенных расчетов могут быть представлены в приведенной ниже таблице.

При составлении данной таблицы выполненные подряд операции удлинения записаны в одной строке (как, например, для первой строки G — А — Н). Если последняя вершина текущего пути совпадает с конечной вершиной Н, то очередной из искомых путей найден. После укорачивания переходим на новую строку таблицы и в ней же записываем результат последующего удлинения пути (если он возможен, как для второй строки G — A — L — Н). Отметим, что при .записи путей

ТекуЩИЙ ПуТЬ Ущ — V[i] — V[2] — ■ ■ ■

G-A-H

G-A-L-H

G-A-L

G-A-R

G-A

G-L-A-H G-L-A-R G-L-A G-L-H G-L

G-R-A-H

G-R-A-L-H

G-R-A-L

G-R-A

G-R

в колонках букв — если только колонки не прерываются — сами буквы упорядочены по алфавиту.

Таким образом, в заданном графе существует 6 различных путей, соединяющих вершины G и Н:

G-A-H,

G-A-L-H,

G-L-A-H,

G-L-H,

G-R-A-H,

G-R-A-L-H.

Отметим, что цепей в графе, соединяющих данные вершины, будет во всяком случае не меньше, чем путей, но тоже конечное число; примером может служить цепь G — А — R — G — L — А — Н, не являющаяся путем. Количество же маршрутов будет бесконечно, поскольку в них допускается повторение и вершин, и ребер.