Глава 8 инструментальные переменные
Глава 8 инструментальные переменные
Задача 8.1
Проверьте формулу (8.5)
3,v = (X,X)-lx'y= (X,Z{Z'Z)'lZ,X)'lX,Z(Z,Z)-lZ'y для оценки, полученной двухшаговым методом наименьших квадратов.
Решение
Имеем X = Z(Z'Z)'1ZX. Тогда
3iv = (x'xy^x'y т (X'ZiZ'Z^Z'ZiZ'ZY^Z'Xy^X'ZiZ'Zy^'y = {X'Z{Z'Z)"xZ'X)~XX'Z{Z'Z)-lZ'y.
Задача 8.2
Докажите, что при т = к оценка (8.5)
\% = {X''Z(Z'zyxz'х)']X'Z(Z'Z)~xZ 'у совпадает с оценкой (8.2)
3IV = (Z'X^Z'y. 230
Решение
При т = к матрица Z'X является квадратной невырожденной матрицей.
Поэтому согласно (8.5) имеем ^ Щ ^^^^г і
3iv = {Z'X)-l{Z'Z){X'Z)'iX,Z{Z'Z)-xZ,y = {Z'X)-lZ'y.
Задача 8.3
Найдите V(/3|V) для оценок (8.2):
J3iy = {ZlX)-lZ'y
и (8.5):
3iv = (X'Z(Z'Z)-xZ'XyXX'Z(Z'Z)-xZ,y.
решение
Рассмотрим сначала случай, когда Z и X — неслучайные матрицы. Тогда
v(3iv) = v{{x'z{z'z)-lz'xyxx'z{z'zylz'y}
= (X'Z(Z'Z)~}Z,X)~{X,Z{Z,ZyxZ,V(y)
х Z{Z'Z)~1Z'X(XfZ{Z,Z)'lZ,Xyl = a2(X'Z{Z'Z)-iZ,Xyi
x X'Z{Z'Z)'xZ'Z{Z'Z)~xZ'X(X'Z(Z'zyxz'x)~l
= g2(x'z{z'z)-xz'xy
Этот случай, однако, не имеет содержательного смысла, так как если рсгрес-соры X не случайные, то сама проблема коррелированное™ регрессоров и ошибок, для решения которой используется метод инструментальных переменных, отсутствует.
Рассмотрим действительно важный случай, когда X и Z случайные. Однако в этом случае мы можем вычислить только асимптотическую матрицу ковариаций оценок.
Сделаем следующие стандартные для метода IV предположения:
Существует plim(l/n)Z'e = О.
Существует plim(l/n)ZfX — конечная матрица максимального ран-Щк га к.
Существует plim(l/?j)Z/Z — конечная положительно определенная I матрица.
Рассмотрим общий случай. Обозначим Р = Z(Z'Z)~lZ тогда
3iv = {Х'РХу'Х'Ру = (3 + {Х'РХУ'Х'Ре.
Заметим сначала, что из 1)-3) вытекает, что следующий предел существует
П равен ПОЛОЖИТеЛЬНО Определенной матрице: щ д ^^Ff
-1
р1їт( ~Z'X ) .
plim (-Х'РХ) = рЦш J /Літ f-Z'Z
Также имеем
plim (^Х'Ре^ = plim i}iZ'Z
-i
plim ( ^Z'er ) = 0.
Отсюда получаем:
plim (/З
IV
= /3 + plim {(X'PX)~l Xі Ре) = /3 + (^)Пт^Х'РХ^ рІІт^Х'Рє
= 0-
Таким образом, мы доказали, что оценка f3lv является состоятельной.
Предположим дополнительно, что n~*f2Z'e — последовательность, удовлетворяющая условиям центральной предельной теоремы. (Это верно, например, в том случае, если инструменты Z не случайные.) Тогда оценка
1
метода инструментальных переменных /3IV имеет асимптотически нормальное распределение, и мы получаем, что вектор
1
^i(0w-P)= -Х'РХ
-1
п
Х'Рє
п
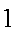
= ( —Х'РХ
1 '^x'z) (z'z
1
п
Z'e
имеет асимптотическое нормальное распределение с асимптотической матрицей ковариаций
a2plim(^~XfPX
Таким образом, мы показали, что
v^(3rv-£)
имеет асимптотическое нормальное распределение с асимптотической матрицей ковариаций
a2plim (^X'Z{Z'Z)-XZ'X
-і
В частном случае (8.2), когда матрица Z имеет ту же размерность, ч* и матрица X, имеет место равенство
(Х'РХ)'1 = (Z'X)-lZ'Z(X'Z)-
так как в этом случае матрица Z'X квадратная, невырожденная. Тогда
асимптотическая матрица ковариациМ имеет вид ■ ^^щЖ
а2/Лип Pl[m (^Z'Z) (X'Z
Задача 8.4
Пусть мы оцениваем регрессионное уравнение
і Уі = 01 + 02Xt +£t, t = 1,...,П
с помощью метода инструментальных переменных, используя переменную Zt как инструмент для х*.
Покажите, что оценки коэффициентов имеют вид
PlIV = У — P2IVX, 02W = ==Г, =77 =7
и являются решениями системы уравнений
Решение
Будем использовать обозначения X = [г &•] для матрицы регрессоров и
 |
(Мы использовали тождество (zt г)'г = 0.) Теперь вычислим 0UV: 2 z'xi'y \%'xz'y nz'xy nz'yx (z'xy пЩ7) -(z'yx пгху)
hz'x — i'xi'z
nz'x n2zx
z'x — nzx
nzx
z'x
{z'x nzx)y [z'y nzy)x _ _
= У P2XVX.
Рассмотрим вторую часть задачи. Оценка f3iv удовлетворяет уравнению
Зїу = (Z'X)~lZ'y, а следовательно, и уравнению ■ ^^^^^^ж
(z'x)3iv = V^^^vj
Запишем последнее уравнение в координатах:
или
| Г л г'х | [|uv | г'уі | ||
| z't z'x | z'y | |||
| •n3uv | + г'х 3aiv = | -г'у | ||
| *'«3||V | f | 2'x/32|V = | z'y | |
что совпадает с системойуказанной в условии задачи.
Задача 8.5
Рассмотрим модель (8.3
у = Х/3 + є, V(e) = <r2/,
в которой ре [рессоры Xtp коррелнрованы с ошибками е*. Пусть Z — некоторая матрица. Преобразуем исходное уравнение, умножив его слева на Z':
Z'y = Z'X(5 + Z\% (*)'
Покажите, что оценка обобщенного метода наименьших квадратов (5.4) для вектора коэффициентов уравнения (*) равна
0GLS = (X'Z(Z'Z)-lZ'X) ~ХX'Z(Z'Z)-xZ'y. I
Сравните результат с формулой (8.5) ДЛЯ оценки метода инструментальных переменных. Ї
Решение I
Введем обозначения: X = Z'X, у = Z'y и є = Z'e. Уравнение (*) в этих обозначениях имеет вид: |
у = Х(3 + є, УЩ = V(Z'e) = Z'V(e)Z = o2Z'Z = П.
Применяя формулу (5.4) для оценок вектора коэффициентов уравнения (*) обобщенным методом наименьших квадратов, получаем следующее выражение:
3gls = (х'п-1Х)-1\%П-1у І = {{Z'X),(Z'Z)-l{Z'X)yz'X){Z,Z)-lZ'y
щ {x'z{z'z)-xz'x)'xx'z{z'z)-'z'y,
которое совпадает с формулой (8.5) для оценки метода инструментальных переменных.
Вадима 8.6 > ^т.
I Пусть переменные у*, связаны (точным) уравнением ^^^^^^^^
Однако вместо точных значений мы наблюдаем измеренные (с ошибками измерений) значения у, — у} 4Щ и zt = z* + vt, где щ ~ iid(0,<т~), Vt ~ iu/(0, ctJJ), ошибки щ и уа независимы при всех t и s. Мы оцениваем методом наименьших квадратов уравнение
, Vt = 01 + 02*1
а) Удовлетворяют ли ошибки в данном уравнении условиям стандартной
і линейной модели?
б) Найти Cov(ztt єt).
в) Найти р im02
Решение
а, б) Подставив выражения для у^, z в исходное уравнение, получаем:
yt ut = 0 402(zt vt)4 или
I Vt = /Зі 4ftZ! + (tit 02Vt).
Таким образом, £t = Щ — 02Vf. В силу условия задачи получаем, что ошибки независимы при всех ( и дисперсия ошибок постоянна
V(e,) = V(t«, fovi) »£ + ДО.
Поскольку рассматривается модель со стохастическими регрессорами, то в понятие «стандартная модель» входит также некоррелированность ошибок с регрессорами. Вычислим коварпацию zt и ef>
Cov{zuet) = Cov(zt* +vt,ut-02vt) = -02ОІ Ф 0.
Обсуждение Сборник задач к начальному курсу эконометрики
Комментарии, рецензии и отзывы
