3.2. задача коммивояжера
3.2. задача коммивояжера
Имеется n городов, занумерованных числами 1,2,...,n. Для любой пары городов задано расстояние (время, путевые расходы) C(ij) > 0 между ними. Поэтому в общем случае C(ij) ф C(j,i). Коммивояжер, выезжая из какого-либо города, должен посетить все города по одному разу и вернуться в исходный город. Необходимо определить такую последовательность объезда городов, при которой длина маршрута была бы минимальной.
Другая интерпретация этой задачи связана с минимизацией времени переналадок при обработке на одном станке партии из n различных деталей. Здесь C(i,j) время переналадки при переходе от обработки детали i к обработке детали j. Требуется найти последовательность обработки деталей, минимизирующую общее время переналадок.
Для записи постановки задачи в терминах целочисленного линейного программирования определим булевы переменные следующим образом: xt] = 1 , если коммивояжер переезжает и i-го города
в j-й; x ц = 0, в противном случае. Тогда задача заключается в отыскании
значений переменных xi}. удовлетворяющих следующим соотношениям:
(3.15)
(3.16) (3.17)
(3.18) (3.19)
п п
II II
— min
і=i j=i
при условиях
п
S Xij = 1, j = 1»-»m (въезд в город j )
SXij = h j=1,...,n
j=1
ui u . + п ■ xH < п 1
j J 4
i =1 п
(выезд из города i )
( i * j )
xij = {0,1}, ut >0, целые, i=1,...,m, j=1,...,n Ограничения (3.18) требуют, чтобы маршрут образовывал контур.
Применение метода ветвей и границ для решения задачи
коммивояжера
Допустимый маршрут х представим как множество упорядоченных пар городов:
X = {(i1,i2), (І2,І3),...,(Іп-1,Іп), (Іп,І1)}.
Каждый допустимый маршрут представляет собой цикл, проходя по которому коммивояжер посещает каждый город ровно один раз и возвращается в исходный город. Каждая упорядоченная пара (ij) является дугой маршрута. Длина F(x) маршрута x равна сумме соответствующих элементов C(i,j). Заметим, что множество всех допустимых маршрутов X содержит (п-1)! элементов.
Обозначим через C = (Cj) матрицу расстояний. Чтобы
J пхп
запретить переезды вида положим C(i,i) = +00 (i=1,.. .,n).
Пусть Pt = min{Cj} , j= (1,...,n) , Qj = mm{CjPt} , i= (1,...,n),
Cij = Cij pi Qj
Тогда C = (Cij) Пусть
пхп
редуцированная матрица.
п
п
d(X) = S P+ S Q сумма констант редуцирования.
i=1 1 j=1 j
Тогда для любого маршрута х = {(i1i2), (j 2i 3),.,(іп 1іп), (іпі1)} є X F(X) = C(i1,i 2) + C(i 2,і3)+...+С(іп,і1) =
C і 2) + C (i 2, i 3)+...+C (іп, i1) + d(X) > d(X) (3.20)
Неравенство (3.20) показывает, что d(X) является оценкой снизу для множества X . Кроме того, после редукции длины всех маршрутов уменьшаются на одну и ту же величину d(X) и, следовательно, оптимальный маршрут, найденный с использованием редуцированной матрицы, оптимален и для исходной задачи.
Ветвление.
Процесс ветвления можно представить в виде дерева, каждая вершина которого соответствует некоторому множеству маршрутов,
являющемуся подмножеством множества X . При этом начальная
вершина соответствует множеству всех маршрутов X .
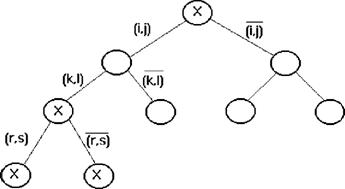
На каждом шаге из числа кандидатов на ветвление выбирается множество X1 с наименьшей оценкой. Оно разветвляется на два подмножества X 11 и X 12 . Подмножество X 11 состоит из всех маршрутов множества X1 , содержащих некоторую выбранную на данном шаге
дугу (r,s),подмножество х2 из всех маршрутов множества X, не содержащих дугу (r,s).
Ребро дерева, соединяющее вершины X1 и X1, помечается (r,s), а ребро дерева, соединяющее X1 и X 2 помечается (r, s).
Пусть C редуцированная матрица, соответствующая вершине
X . Опишем способ выбора дуги (r,s). Он основан на стремлении сделать оценку d(поменьше, а оценку d(X2)побольше, для того, чтобы увеличить вероятность выбора для дальнейшего ветвления множества X1. Стремление к уменьшению d(X^ приводит к выбору такой дуги (u,v), для которой
C Vv) = 0 (3.21)
поскольку все маршруты множества X1 содержат дугу (|i,v). Стремление же увеличить d(X2) приводит к выбору среди дуг, удовлетворяющих условию (3.21) той дуги, для которой значение функции
©0,v) = min С С"* р)+ min С V,v)
p:pфv о-.офц максимально, т.е.
0( r, s) = max {0(|,v)}.
Смысл введения функции 0 состоит в том, что величина 0(|, v)
является оценкой снизу для длины любого маршрута из X , не содержащего дуги (|,v), так как величина 0(|, v) выражает дополнительное расстояние, которое коммивояжер проезжает в случае, когда в маршрут не включена дуга (|,v).
Построение редуцированных матриц С 2 и С1 и вычисление
оценок снизу
Положим
c2 (uj)
Искомая редуцированная матрица С 2 получается из С2 с
помощью описанной выше процедуры редуцирования. Сумма констант редуцирования равна при этом 0(r, s), а величина
d (X 2) = d (XV) + 0(r, s) является оценкой снизу для целевой функции F(x) на множестве
X2. і
Рассмотрим теперь множество X1. Все маршруты из этого множества содержат дугу (r,s). Найдем максимальный связанный путь, который принадлежит всем маршрутам множества X и содержит дугу
(r,s). Пусть этот путь начинается в городе m и заканчивается в городе t (может быть, m=r или t=s, или то и другое одновременно).Чтобы запретить подцикл, начинающийся и заканчивающийся в m, положим
CC1(t, m) = +оо. Остальные элементы матрицы С1 полагаем равными соответствующим элементам матрицы С , при этом строку, соответствующую городу г и столбец, соответствующий городу s, в матрицу ( не включаем, поскольку все маршруты из X1 содержат дугу (r,s).
Редуцированная матрица расстояний С1 для вершины X1 получается из матрицы ((1 с помощью операции редуцирования. При этом оценка снизу для функции F(x) на множестве X1 вычисляется по формуле
d(Хі) = d(Xі) + т , где т сумма констант редуцирования.
Формирование списка кандидатов на ветвление.
После вычисления каждой из оценок d(Хг) (i=1,2) следует
проверить, не состоит ли множество Xі из единственного маршрута.
Если в каждой строке и в каждом столбце матрицы С1 оказалось лишь
по одному элементу, отличному от +оо, то множество Xі содержит
единственный маршрут, длина которого равна d(Xі). В этом случае верхняя граница Z0 (наименьшее из уже вычисленных значений F(x)
полагается равной минимуму из предыдущего значения Z 0 и d (X,), т. е.
Z 0 = min { Z 0, d ( X Если Xі содержит более одного маршрута и d(X;) меньше текущего значения Z0, то множество Xі включается в число
кандидатов на ветвление. Остановка производится, если наименьшая из оценок снизу кандидатов на ветвление не меньше текущего значения
Z0.
Пример. Решить методом ветвей и границ задачу коммивояжера с матрицей
| 10 | 25 | 25 | 101 | ||
| 1 | 10 | 15 | 2 | ||
| С= | 8 | 9 | 20 | 10 | |
| 14 | 10 | 24 | 15 | ||
| V10 | 8 | 25 | 27 |
Возьмем в качестве произвольного допустимого маршрута
{(1,2),(2,3),(3,4),(4,5),(5,1)}. Тогда F(Хо) = 10+10+20+15+10 =
 |
| 'с 0 6 3 | 0 > |
| 0 с 0 2 | 1 |
| 0 1 с 0 | 2 |
| 4 0 5 с | 5 |
| V 2 0 8 7 | со) |
C
Нижняя граница d(X) = 10+1+8+10+8+9+12=58. Данное значение является нижней границей длин всех маршрутов. Заметим, что в идеальном случае поиск решения заключался бы в выборе ровно одного нулевого элемента в каждой строке и каждом столбце. Другими словами, если бы такой маршрут нулевой длины мог бы быть найден, то длина оптимального маршрута равнялась бы 58. Исходя из верхней и нижней границ можно заключить, что 58 < F(х*) < 65 .
Выберем дугу (r,s) с помощью вычисления значений функции 0Qi,v).
0(1,2)=0, 0(2,1)=0, 0(3,1)=0, 0(4,2)=4, 0(1,5)=1, 0(2,3)=5, 0(3,4)=2, 0(5,2)=2.
Следовательно, 0(r,s) = (2,3). Осуществим разбиение (ветвление). Правое подмножество X2 будет содержать все маршруты, которые
исключают дугу (2,3). Поэтому C 2(2,3) = +с.
с2
| 'о 0 6 3 | 0 Ї | 0 | 'со 0 6 3 01 | ||
| 0 оо 2 | 1 | 0 | 0 оо 2 1 | ||
| 0 1 о 0 | 2 | 0 | 0 1 о 0 2 | ||
| 4 0 5 о | 5 | 0 | 4 0 5 о 5 | ||
| ч 2 0 8 7 | о) | 0 | v 2 0 8 7 о) | ||
| 0 0 5 0 0 | |||||
| о013 | |||||
| 0оо2 | 1 | ||||
| 01о0 | 2 | = | C 2 | ||
| 400о | 5 | ||||
| 2037 | о) | ||||
Оценка снизу для правого подмножества X2 определяется следующим образом:
d(X2) = d(X ) + ©(2,3) = 58 + 5 = 63 < Z0.
Левое подмножество Xi будет содержать маршруты, которые
всегда включают дугу (2,3), и поэтому вторая строка и третий столбец в матрицу Ci не включаются. В результате будем иметь матрицу на
единицу меньшего размера. Далее необходимо положить c1 (3,2) = +о, чтобы запретить подцикл {(2,3),(3,2)}. В результате получим матрицу
12 4 5 1 'о 0 3 01
C1
0о02 40о5
Ч 2 0 7 о)
C1
Оценка снизу для левого подмножества
d(X1) = d(X ) + т = 58 + 0 = 58 < Z0. В списке кандидатов на ветвление множества X1 и X2 . Так как
d(X 1) < d(X2 ), следовательно, будем производить ветвление множества X1 . Выберем дугу (г, s) с помощью значений функции 0(u,v) для матрицы Q ^ .
0(1,2) = 0, 0(1,5) = 2, 0(3,1) = 2, 0(3,4) = 3, 0(4,2) = 4, 0(5,2) = 2. Следовательно, 0(r,s) = 4, (r,s) = (4,2).
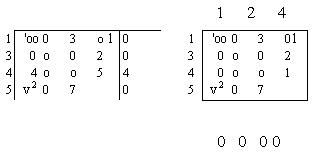 Правая подматрица: 12 4 5
Правая подматрица: 12 4 5
Оценка снизу для правого подмножества: d (X4) = d (X1) + 0(4,2) = 58 + 4 = 62 < Z 0
Левая подматрица:
Левое подмножество X3 будет содержать маршруты, которые
всегда включают дугу (4,2), и поэтому четвертая строка и второй столбец в матрицу C3 не включаются. В результате будем иметь
матрицу на единицу меньшего размера. Далее необходимо положить С3 (3,4) = +оо, чтобы запретить подцикл {(4,2),(2,3),(3,4)}. В результате
получим матрицу

C
d(X3) = d(X1) + т = 58 + 5 = 63 < Z0.
В списке кандидатов на ветвление множества X3 , X4 , X2 .
Минимальная нижняя оценка оказалась у множества X4 ,
следовательно, для дальнейшего разбиения выбираем множество X4 .
Определим дугу (r,s) с помощью значений функции 0(u,v) для матрицы C 4 .
0(1,2) = 0, 0(1,5) = 1, 0(3,1) = 0, 0(3,4) = 3, 0(4,1) = 1, 0(5,2) = 2. Следовательно, 0(r,s) = 3, (r,s) = (3,4).
 | 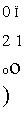 | ||
12 4 5 1 (о 0 3 0^|
Се
0 оооо 2 0 оооо 1 2 0 7 о)
1245
С,
Оценка снизу для правого подмножества:
d (X6) = d( X4) + 0(3,4) = 62 + 3 = 65 = Z0-Следовательно, множество Xе исключаем из списка.
Левая подматрица:
Левое подмножество X5 будет содержать маршруты, которые
всегда включают дугу (3,4), и поэтому третья строка и четвертый столбец в матрицу С5 не включаются. В результате будем иметь
матрицу на единицу меньшего размера. Далее необходимо положить £5 (4,2) = +оо, чтобы запретить подцикл {(2,3),(3,4), (4,2)}, однако это
условие оказалось уже выполненным. В результате получим матрицу
125
С5
1(
4
о0 0о
0 Ї
1
2 0 о)
Оценка снизу для левого подмножества:
d( X5) = d( X4) + т = 62 + 0 = 62 < В списке кандидатов на ветвление множества X3 , X5 , X2 . Минимальная нижняя оценка оказалась у множества X5 , следовательно, для дальнейшего разбиения выбираем множество X5 .
Определим дугу (r,s) с помощью значений функции 0(u,v) для матрицы С5 . 0(1,2)=0, 0(1,5)=1, 0(4,1)=3, 0(5,2)=2.
Следовательно, 0(r,s) = 3, (r,s) = (4,1).
Правая подматрица:
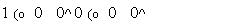 125
125
12 5 1 (о 0 0 ^
С8
оо
20
1
о)
20
0
с)
сс
00
0
с)
2 0 0
Оценка снизу для правого подмножества:
d (X8) = d( X5) + 0(4,1) = 62 + 3 = 65 = Следовательно, множество X8 исключаем из списка.
Левая подматрица:
Левое подмножество X7 будет содержать маршруты, которые
всегда включают дугу (4,1), и поэтому четвертая строка и первый столбец в матрицу С7 не включаются. В результате будем иметь
матрицу на единицу меньшего размера. Далее необходимо положить £7 (1,2) = +о, чтобы запретить подцикл {(2,3),(3,4),(4,1),(1,2)}.
2 5
1
с
0 Ї
С7 5І0 о) С
Оценка снизу для левого подмножества: d(X7) = d( X5) + т = 62 + 0 = 62 < Z0. В списке кандидатов на ветвление множества X3 , X7 , X2 . Множество X7 содержит единственный маршрут с минимальной
нижней оценкой, поэтому задача решена.х1={(1,5)(5,2)(2,3),(3,4),(4,1)} = x* Z0 = F( x*) = 10 + 8 + 10 + 20 + 14 = 62 . Представим процесс решения в виде дерева.
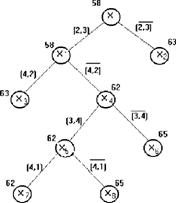
Домашнее задание 3.2.
Решить методом ветвей и границ следующую задачу коммивояжера:
| оо | 31 | 15 | 19 | 8 | 55 | г | 2. о | 19 | 25 | 11 | 2 | 55 | "і | |||
| 19 | о | 22 | 31 | 7 | 35 | 37 | о | 26 | 58 | 21 | 43 | |||||
| 25 | 43 | о | 53 | 57 | 16 | 10 | 50 | о | 39 | 22 | 3 | |||||
| 5 | 50 | 49 | о | 39 | 9 | 38 | 39 | 24 | о | 38 | 45 | |||||
| 24 | 24 | 33 | 5 | о | 14 | 27 | 9 | 32 | 9 | о | 2 | |||||
| V 34 | 26 | 6 | 3 | 36 | о | 33 | 48 | 60 | 53 | 1 | о | J | ||||
| 3. | 4. | |||||||||||||||
| ^ оо | 16 | 13 | 35 | 41 | 52 | г | о | 39 | 45 | 2 | 51 | 33 | ||||
| 19 | о | 29 | 31 | 26 | 18 | 30 | о | 20 | 33 | 40 | 35 | |||||
| 57 | 51 | о | 44 | 51 | 7 | 54 | 16 | о | 55 | 22 | 56 | |||||
| 5 | 40 | 32 | о | 14 | 16 | 19 | 36 | 25 | о | 18 | 43 | |||||
| 33 | 41 | 28 | 3 | о | 53 | 29 | 8 | 8 | 12 | о | 25 | |||||
| і9 | 54 | 24 | 10 | 41 | о | 16 | 47 | 31 | 14 | 8 | о J | |||||
| 5. |
Обсуждение Исследование операций в экономикеКомментарии, рецензии и отзывы 3.2. задача коммивояжера: Исследование операций в экономике, И.Н. Мастяева, 2003 читать онлайн, скачать pdf, djvu, fb2 скачать на телефон Рекомендовано Учебно-методическим объединением по образованию в области статистики в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специальности 061700 «Статистика» и другим экономическим специальностям.
| |||||||||||||||
