2.2. основные положения теории двойственности

2.2. основные положения теории двойственности

Прямая задача Двойственная задача

max f (x) = (С, X) min g(у) = (у, й)

A x = b yA > С

x > 0 у не ограничен в знаке

Теорема 1. Пусть x, у планы соответственно прямой и двойственной ЗЛП, тогда

f (x) < g(y) (2.12)

Теорема 2. Пусть x, у- планы соответственно прямой и

двойственной ЗЛП и f (x ) = g(у ), тогда x , у решения соответственно прямой и двойственной задач.

Теорема 3. Если прямая (двойственная) ЗЛП имеет конечное решение, то и двойственная (прямая) ЗЛП имеет решение, причем

max f ( х) = min g(y) (2Л3)

Если прямая (двойственная) ЗЛП не имеет решения, то и двойственная (прямая) ЗЛП не имеет решения.

Теорема 4. Планы х , y соответственно прямой и двойственной ЗЛП являются оптимальными тогда и только тогда, когда

х *(y *A C) = О (2.14) Условия (2.14) называются условиями дополнительной нежесткости.

Замечание 1. Для основной ЗЛП и двойственной к ней ЗЛП условия нежесткости имеют вид:

y*(Ax*b) = 0 (2.15) х (y A C) = О

Замечание 2. Если прямая ЗЛП записана не в канонической форме, то условия дополнительной нежесткости для этой ЗЛП и двойственной к ней ЗЛП могут быть записаны в следующем виде:

* т если х| > О, то ^ аг3Уг = cj

i=1

n *

если YjауХ* < bi, то yi = О,

если yi > 0, то Y aijX* = bi, (2.16)

j=1

если Y aiJyi* > Ci, то Xj = 0.

i=1

Получение оптимального плана двойственной задачи на

основании теоремы 4.

Пример 2.5. Рассмотрим задачу: min(2 х1 + 4 х2)

3х1 + х2 > 3

4х1 + 3х2 > 6 (2.17)

х1 + 2 х2 < 3

Х1,2 > 0

Ее решение x = (3/2; 0), minf (x) = 3. Найдем решение задачи, двойственной к (2.17), используя теорему 4. Запишем двойственную к (2.17) задачу:

(2.18)

max^ + + 3У3) 3У1 + 4У2 + У3 < 2 У1 + 3 У2 + 2 У3 < 4 У1,2 > 0, У3 < 0

то

и так как

Применяем соотношение (2.16). Так как х1 =3/2 > 0, 3у1 +4у2 +у3 =2. Далее, так как 3х1 +х2 =9/2+0 > 3, то у1 =0, х1 +2х2 =3/2+0 < 3, то у3 =0. Итак, имеем: 3у1*+4у2*+у3*=2, у1*=у3*=0,

т.е. вектор у = (0; 1/2; 0) является решением задачи (2.18) на

основании теоремы 4. Вычислим g(y ) = 6х 1/2 = 3 = f (x), что соответствует утверждению теоремы 3.

Пример 2.6. Найти решение прямой и двойственной задачи.

Прямая задача.

max f (x)= 5 Х1 +12Х2 +4 Х3 Х1 +2 Х2 +3Х3 < 10

2Х1 Х2 +3Х3 = 8

Х2,3 > 0

Х1 не ограничена в знаке

Двойственная задача.

min g (У)=10У1+8 Y2 Y1 +2 Y2 = 5 (а) 2 Y1 - Y2 > 12 (б) Y1 + 3 Y2 > 4 (в) Y1 > 0 (г) У2 не ограничена в знаке.

Двойственная задача содержит две переменные, т. е. решать графически (рис.2.1)

ее можно

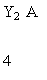Puc.2.1

Как видно из рис.2.1, область допустимых решений планов двойственной ЗЛП Q представляет собой отрезок АВ, лежащий на прямой Y1 +2 Y2 = 5, так как первое ограничение задается в виде равенства. Передвигая линию уровня функции 10 Y1 +8 Y2 = const в направлении, противоположном вектору b =(10,8), получаем точку А, в которой достигается минимум функции g(y). Находим координаты точки А, которая является пересечением двух прямых:

Y1 +2 Y2 = 5

2 Y1 Y2 = 12, откуда у; =29/5; Y2* =-2/5 и g (Y *) =54 4.

Ипользуя теорему 4, находим решение исходной задачи. Так как Y* >0 и Y2 <0, то оба ограничения прямой задачи имеют вид строгих равенств.

Х1 +2 Х2 +3Х3 = 10 (2.19) 2Х1 Х2 +3Х3 = 8

Так как третье ограничение двойственной задачи выполняется в виде строгого неравенства ( 29/5 6/5 = 24/5 > 4) , то X* =0. Решая систему (2.19), получаем:

х; = 26/5; X *2 = 12/5; X3* =0; f( X *) = 54,8.

Получение оптимального решения двойственной задачи из симплекс-таблицы решения прямой задачи.

Пусть прямая задача имеет вид основной ЗЛП max f (x) = (C, x)

Ax = b (2.20) x > 0 , b > 0.

Двойственная к ней ЗЛП имеет вид

min g(у ) = (у,b)

yA > C (2.21)

у > 0.

Предположим, что ЗЛП (2.20) имеет решение. Решения обеих задач могут быть записаны в виде :

x * = Xn(s) = B-1 b ; у * = CNs) B-1,

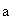С а( S)

( S ) ^ 1 n+m

где

=( а

(S)

n +1

-(S) )

а( S)

\^ mn+1

а

(S)

матрица, обратная для базисной подматрицы BS. Матрица Bsl подматрица K(s) расположена на месте единичной подматрицы в исходной матрице K(0). Кроме того, можно показать, что

А(й = У:, i = im, (2.22) откуда следует, что i -я компонента у i решения двойственной ЗЛП

есть (n + і)-я симплекс-разность матрицы K(s), определяющей оптимальный план исходной ЗЛП, а j-я симплекс-разность матрицы K(s) (j = 1, n) равна разности между левой и правой частью ограничений двойственной ЗЛП:

n

A(s) = (У*,-j) Cj = Z ajyi~ Cj, j = . (2.23)

j=i

Пример 2.7. Решить следующую ЗЛП:

max ( 4Х1 + Х2 + 2Х3 +3 Х4 )

Х1 + 2 Х2 +3Х3 Х5 + Х7 =50

-3Х2 +3Х3 + Х4 +5Х5 + 4Х7 =40 (2.24)

4 Х2 + Х5 + Х6 Vi Х7 =24 Xj > 0, j = ї/7.

Найти решение задачи двойственной к ЗЛП (2.24). Так как расширенная матрица

K

(0).

(1 2 3 0 -1 0 1 0 3 112 0 4 0 4 0 0 1 1 -1/2

50 ^

10 24

N = (1, 4, 2); Xn(1) = (38, 28, 6),

X * = ( 38, 6, 0, 28, 0, 0, 0); f( X *) = 242.

Запишем задачу, двойственную к (2.24)

системы линейных уравнений (2.24) является К-матрицей, то ЗЛП (2.24) можно решить симплекс-методом. Результаты решения приведены в таблице.

min(50Y1+10Y2+24Y3) Y1 > 4

Y1 3 Y2 + 3 Y3 > 1

Y1 + Y2 + 4 Y3 > 1

Y2>3

-Y1 +2 Y2 + Y3 > 0

Y3 > 0

Y1 + 4 Y2 V2 Y3 > 0 Y1-3 не ограничены в знаке.

(2.25)

(2.26)

(2.27).

Ограничения (2.27) являются избыточными, следовательно, их можно отбросить.

Находим решение ЗЛП (2.25) по формуле

у у=Cn (1) B-1 = (4, 3, 1)

(1 0 -1/2^ 0 1 3/4 0 0 1/4

= (4, 3, 1/2),

или (2.22):

7 = (A? + Q, A? + C4, A« + С6 )=(0+4,0+3, y2 +0) = (4, 3, 1/2) g( 7)= 50*4 + 10*3 + 24* V2 =242