Тема 5.2 учет гетероскедастичности

Тема 5.2 учет гетероскедастичности

Такой вид нарушений стандартных предположений, как неоднородность дисперсий ошибок (гетероскедастичность, heteroscedasticity), характерен для статистических данных, относящихся к одному моменту времени, но собранных по различным регионам, предприятиям, социальным группам (перекрестные данные). Неоднородность дисперсий возникает также как результат тех или иных структурных изменений в экономике (например, связанных с мировыми экономическими кризисами). Пример 4.2.1 как раз иллюстрирует подобную ситуацию: в нем резкое возрастание абсолютных величин остатков относится к периоду глобального нефтяного кризиса.

Последствия неоднородности дисперсий ошибок (гетероскедастич-ности):

оценки дисперсий случайных величин #15 вр (оценок коэффициентов линейной модели), построенные на базе стандартных предположений, оказываются смещенными;

построенные на базе стандартных предположений доверительные интервалы для в19 вр не соответствуют заявленным уровням значимости;

вычисленные значения tи F-отношений уже нельзя рассматривать как наблюдаемые значения случайных величин, имеющих tи F-pacnpe-деления, соответствующие стандартным предположениям. Поэтому сравнение вычисленных значений tи F-отношений с квантилями указанных tи F-распределений может приводить к ошибочным статистическим выводам по поводу гипотез о значениях коэффициентов линейной модели.

ПРИМЕР 5.2.1

Для исследования вопроса о зависимости количества руководящих работников от размера предприятия были собраны статистические данные по 27 промышленным предприятиям (табл. 5.9). Обозначим:

xt — численность персонала на і-м предприятии, у і — количество руководителей на і-м предприятии.

Оценим линейную модель наблюдений

у{=а + 0х{+€п / = 1,..., 27.

В ходе регрессионного анализа получим R2 = 0.776 и результаты, приведенные в табл. 5.10.

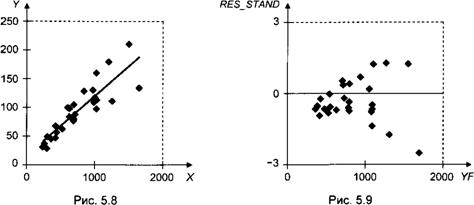
На рис. 5.8 приведена диаграмма рассеяния с подобранной прямой у = 14.448 + 0.105х, на рис. 5.9 — график зависимости стандартизованных

Єостатков ct =— от значений yt = 14.448 + 0.105*,. S

Похоже, что имеет место тенденция линейного возрастания абсолютных величин остатков с ростом j), соответствующая наличию приближенной зависимости вида D(st) = а? = <J2xf для дисперсий ошибок. Чтобы погасить такую неоднородность дисперсий, разделим обе части соотношения Уі = а + рХі + st на*,-:

X; Xi Xi

т.е. перейдем к модели наблюдений

у* =Р + ах* +є*,

где

* У і * 1 * Є:

Уі=—> *,■= — — •

xt xt xt

Если действительно выполняется соотношение D(€t) = erf = <т2х?, то в преобразованной модели

= 0, D(s*) = D(8i) = cj

т.е. неоднородность дисперсий ошибок преодолевается.

Результаты оценивания преобразованной модели приведены в табл. 5.11.

В исходных переменных это соответствует модели линейной связи

у = 3.803 + 0.121 х.

Отметим уменьшение оцененных стандартных ошибок оценок обоих параметров а и р. Именно на эти значения следует опираться при построении доверительных интервалов для параметров. Средними точками этих интервалов будут соответственно а 3.803 и р 0.121. График на рис. 5.10 показы

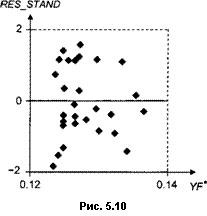вает характер зависимости стандартизованных остатков в преобразованной модели от у*. На этот раз неоднородности дисперсий остатков (по крайней мере, явной) не обнаруживается.■

Проанализируем наши действия при оценивании преобразованной модели. Оценки коэффициентов, приведенные в табл. 5.11, получены применением метода наименьших квадратов к модели наблюдений^* = /?+ ах] + є], т.е. путем минимизации суммы квадратов

которую (зная, что обозначают переменные со звездочками) можно записать в виде:

\%i J

Обозначив теперь wl■,= —г, заметим, что задача минимизации суммы квадратов отклонений в преобразованной модели равносильна задаче минимизации взвешенной суммы квадратов отклонений в исходной (непреобразован-ной) модели. Величина wi интерпретируется в этом контексте как вес, приписываемый квадрату отклонения в /-м наблюдении. Этот вес будет тем меньше, чем больше значение xf, которое в силу наших предположений пропорционально дисперсии случайной ошибки D(st) = of = a2 xf в /-м наблюдении. Следовательно, чем больше дисперсия случайной ошибки єі9 тем меньше вес, с которым входит квадрат отклонения в /-м наблюдении в минимизируемую сумму.

С учетом того что оценивание преобразованной модели наблюдений сводится к минимизации суммы

п

рассмотренный метод оценивания обычно называют взвешенным методом наименьших квадратов, хотя точнее его следовало бы называть методом наименьших взвешенных квадратов. В учебнике (Магнус, Катышев, Пере-сецкий, 2005) он называется методом взвешенных наименьших квадратов, что ближе к англоязычному варианту: WLS — weighted least squares в отличие от OLS — ordinary least squares.

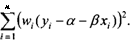В этом случае вес приписывается не квадрату отклонения, а самому отклонению (уі а J3 х(). Разумеется, в рассмотренном примере при таком определении веса последний будет равен: wt = —.

Об этом следует помнить при спецификации весов в процедурах, реализующих взвешенный метод наименьших квадратов.

Обратим теперь внимание на то, в каком виде выдается информация о результатах применения взвешенного метода наименьших квадратов на примере пакета Econometric Views. При этом используем данные примера 5.2.1 о зависимости количества руководящих работников от размера предприятия. Согласно только что сделанному замечанию, при обращении к процедуре оценивания взвешенным методом наименьших квадратов в условиях нашего

примера специфицируем веса как w = — .

х

Протокол оценивания приведен в табл. 5.12. В этом протоколе приводятся значения двух видов статистик:

взвешенные статистики (weighted statistics) — статистики, основанные на остатках, получаемых по взвешенным данным, т.е. на остатках е*=у*-/3ах* в преобразованной модели;

невзвешенные статистики (unweighted statistics) — статистики, основанные на остатках ut = yt aWLS j3WLSxi9 т.е. на отклонениях наблюдаемых значений объясняемой переменной у от значений, предсказываемых линейной моделью связи, в качестве параметров которой берутся их оценки, aWLS9 pWLS, полученные в преобразованной модели.

Отметим весьма низкое (0.02696) значение коэффициента детерминации в преобразованной модели. Однако это обстоятельство не должно нас волновать — линейная связь в преобразованной модели значима, о чем говорят весьма высокое значение F-статистики, равное 180.7789, и соответствующее ему Р-значение 0.0000 (см. Weighted statistics). В конечном счете нас инте

ресует значение R2, находящееся в части протокола, соответствующей не-взвешенным статистикам, а это значение достаточно велико (0.758).

Отметим также, что приведенные в начале табл. 5.12 значения оценок параметров, их стандартных ошибок и ^-статистик, а также Р-значения соответствуют величинам, полученным на стадии оценивания преобразованной модели.

Заметим, наконец, что значение R2 = 0.758, указанное в числе невзвешенных статистик, отличается от значения R2 = 0.776, полученного при оценивании исходной (непреобразованной) модели наблюдений. Причина этого, разумеется, в том, что при вычислении значения R2 = 0.776 использовались остатки

где d9j3—оценки наименьших квадратов параметров исходной модели, полученные без использования взвешивания отклонений.

Взвешенный метод наименьших квадратов предполагает известной форму зависимости дисперсий случайных ошибок от объясняющих переменных. В примере 5.2.1 мы предположили, что такая зависимость имела вид: D(st) = а? = <j2 х ?, ориентируясь лишь на график зависимости стандартизованных остатков ct =— от прогнозных значений j),. Некоторым подспорьем S

при определении формы зависимости здесь может стать применение критерия Глейзера (Glejser test). Этот критерий, не вполне оправданный с теоретической точки зрения и предполагающий наличие большого количества наблюдений, состоит в следующем. После оценивания методом наименьших квадратов основной модели производится оценивание вспомогательной модели, объясняющей изменчивость абсолютных величин полученных на первом этапе остатков изменчивостью значений одной из объясняющих переменных. Если X— такая объясняющая переменная, то более или менее оправданным является рассмотрение моделей следующего вида:

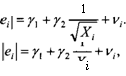В рамках каждой из этих моделей проверяется гипотеза о равенстве 0 коэффициента у2. Если эта гипотеза не отклоняется, то гетероскедастичнось соответствующей формы не обнаруживается. При отклонении этой гипотезы можно с определенными оговорками ориентироваться на соответствующую функциональную форму зависимости а отХ.

Как отмечалось выше, результатом неоднородности дисперсий случайных ошибок в модели наблюдений является смещение оценок дисперсий случайных величин ^, ^. В то же время наличие такого нарушения стандартных предположений оставляет сами оценки вх, вр несмещенными. (Доказательство оставляем для самостоятельной работы, см. также разд. 6.) В связи с этим один из методов коррекции статистических выводов при неоднородности дисперсий ошибок состоит в использовании обычных оценок наименьших квадратов (OLS-оценок, ordinary least squares estimates) вІ9 вр коэффициентов 0l9 вр вместе со скорректированными на гетероскедас-тичность оценками стандартных ошибок s§. Один из вариантов получения скорректированных на гетероскедастичность значений s§. был предложен

Уайтом и реализован в ряде пакетов статистического анализа данных, в том числе в пакете EViews. При этом удовлетворительные свойства оценки Уайта (White estimator) гарантируются только при большом количестве наблюдений.

Оценка Уайта строится на базе явного выражения для ковариационной

матрицы вектора в оценок коэффициентов линейной эконометрической модели, в которой ошибки хотя и имеют нулевые математические ожидания, но не являются одинаково распределенными и/или взаимно независимыми случайными величинами, так что

Cov(s) = V,

где V — симметричная, положительно определенная матрица, Уф а21п. В такой ситуации имеем:

Cov0)= Cov((XTXylXTy) = (XTXylXTCov(y)X(XTXyl = = (XTX)'XTVX)(XTXy Если имеет место чистая гетероскедастичность, то

(7Х • • • U

F = diag(<T12,...,<7„2)= : : ,

О а2п

и матрица Cov(O) содержит п неизвестных параметров — столько же, сколько имеется наблюдений. Тем не менее можно получить состоятельную оценку матрицы Cov(0), а значит, и состоятельные оценки для дисперсий оценок коэффициентов и стандартных ошибок оценок коэффициентов s#, если заменить в матрице V неизвестные значения дисперсий ошибок of, а2 на квадраты остатков, полученных в результате оценивания модели обычным методом наименьших квадратов, т.е. на е2, е2. Это приводит к оценке Уайта.

ПРИМЕР 5.2.2

Используем данные из предыдущего примера, но применим для их анализа последнюю процедуру, воспользовавшись пакетом EViews.

Согласно этой процедуре оцениваем коэффициенты а и /? обычным методом наименьших квадратов, так что в качестве оценок берутся а = 14.448 и Р = 0.105. В качестве оценок стандартных ошибок sa и Sp вместо sa = 9.562 и Sp = 0.011, полученных выше при оценивании модели обычным методом наименьших квадратов, берем значения оценок Уайтаsd = 10.633 и^ = 0.018.

Бросающееся в глаза значительное различие оценок для параметра а при применении двух рассмотренных методов (3.803 и 14.448) в действительности не столь уж удивительно, поскольку оценки стандартной ошибки для а, полученные каждым из двух методов, довольно высоки (sd = 4.570 и s^ = 10.633 соответственно).■

Избавиться от неоднородности дисперсий ошибок в ряде случаев позволяет переход к логарифмам объясняемой переменной.

ПРИМЕР 5.2.3

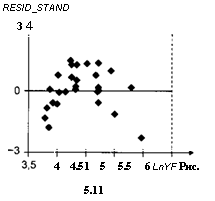
По данным, использованным в примерах 5.2.1 и 5.2.2, оценим модель наблюдений yt = а + fix; +єі9 / = 1,..., 27. График зависимости стандартизованных остатков, полученных при оценил

вании этой модели, от предсказанных значений In у. приведен на рис. 5.11.

RESID_STAND 2

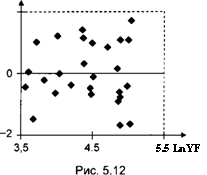
Он указывает на неправильную спецификацию модели, связанную с возможным пропуском квадратичной составляющей х2. Оценивание расширенной модели наблюдений, включающей дополнительную объясняющую переменную х2, приводит к остаткам, обнаруживающим существенно более удовлетворительное поведение (рис. 5.12). Результаты оценивания расширенной модели приведены в табл. 5.13.

Таблица 5.13

Таким образом, использовав разные преобразования переменных, получили две альтернативные оцененные модели связи между переменными х и у:

j = 3.803 + 0.121x и 1п>; = 2.851 + 0.003х-1.1-10"6х2.

Первую из этих двух моделей можно предпочесть из соображений простоты интерпретации. ■

КОНТРОЛЬНЫЕ ВОПРОСЫ

К каким последствиям приводит наличие неоднородности дисперсий ошибок (гете-роскедастичность) в линейной эконометрической модели?

Какими способами можно получить корректные статистические выводы при наличии гетероскедастичности?

В чем состоит взвешенный метод наименьших квадратов? Каким образом выбираются веса? Как еще можно трансформировать модель для преодоления последствий гетероскедастичности?

Можно ли при наличии гетероскедастичности получить корректные статистические выводы, не прибегая к преобразованию переменных?