4.1. модель мультисчета в схеме простых процентов

4.1. модель мультисчета в схеме простых процентов

Если вкладчик открывает несколько срочных вкладов, то он инициирует несколько одновременных кредитных сделок. С точки зрения банка, открытие вкладов различными вкладчиками также есть некоторое семейство сделок.

Каждая из таких сделок или отдельный накопительный счет могут анализироваться с помощью описанных в предыдущих параграфах методов. Однако будет естественным желание получить некоторые обобщенные (интегральные) характеристики семейства сделок или счетов. Так, вкладчика, открывшего несколько счетов, может интересовать вопрос об общей сумме накоплений на этих счетах. Точно так же

инвестору, желающему приобрести портфель государственных краткосрочных облигаций (ГКО) с заданными сроками погашения, например для обеспечения тех или иных будущих платежей, необходимо знать величину требуемого капитала, т.е. стоимость такого портфеля.

В простейшем случае способ построения такой модели сводится к перечислению всех сделок, счетов, ценных бумаг и т.д. с одновременным указанием их временных и финансовых характеристик, необходимых для определения одной или нескольких обобщенных показателей.

Говоря о наборе или семействе объектов, математики часто называют их векторными объектами или векторами. Для задания вектора необходимо указать все его компоненты или элементарные составляющие и порядок их следования. Тогда открытие п накопительных счетов описывается вектором их начальных состояний

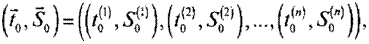где финансовое событие ,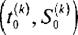j задает начальное состояние k-vo счета; здесь и ниже для упрощения записи используется обозначение

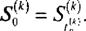
Векторную модель для конечного набора накопительных счетов назовем моделью мультисчета, а отдельные счета, составляющие муль-тисчет, т.е. его компоненты, — субсчетами.

Таким образом, начальное состояние мультисчета представляет собой просто дискретный финансовый поток. В принципе в качестве начального состояния может быть взят любой поток CF:

(f0A)=cf.

В этом случае говорят, что мультисчет порожден потоком CF.

Ниже более подробно рассмотрим именно эту модель. Однако термин «модель мультисчета» будем применять и в более общей ситуации, говоря и о других семействах кредитных сделок, в частности при формировании портфеля ценных бумаг инвестором, кредитного портфеля банком и т.д.

Возвращаясь к собственно модели мультисчета, заметим, что динамика финансового процесса, связанного с субсчетом к (к = 1, 2,п), описывается основной формулой простых процентов:

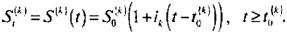(4.1)

Кроме того, начальный момент, начальная сумма и, что наиболее существенно, процентная ставка могут быть различными для различных субсчетов.

Возникает вопрос: в каком смысле можно говорить о состоянии мультисчета в данный момент времени! На первый взгляд это просто вектор, компоненты которого являются состояниями субсчетов, а именно вектор

Однако есть некоторая тонкость, связанная с тем, что, строго говоря, состояние k-то субсчета определено только для моментов времени t>t^K Поскольку начальные мбменты у различных субсчетов различны, то заранее неясно, для каких t считать определенным вектор состояний.

Один из способов разрешения этой коллизии состоит в так называемом тривиальном расширении — приеме, часто используемом в математике и ее приложениях. Будем считать состояния субсчетов всюду определенными, принимая, что субсчет к — нулевой до момента его открытия (к = 1, 2,..., п). Тогда в качестве нового состояния субсчета к примем

5*4=1

Sf при/>/<" О при I < (J*1

(4.2)

В этом случае становится корректным определение состояния мультисчета как вектора

для любого момента времени. Тогда с учетом (4.1) и (4.2) векторная динамика мультисчета будет описываться системой уравнений

s,

('-'»")) при

О приґ</;;, £ = 1,2,...,л

(4.3)

Описав состояния мультисчета и динамику его изменения, введем те обобщенные характеристики, с неформального определения которых начался этот параграф.

Назовем полной величиной или полной суммой мультисчета в момент времени г сумму состояний его субсчетов: (4.4)

Полная величина (сумма) мультисчета (или коротко полный счет) в каждый момент времени характеризует общую сумму накоплений инвестора, открывшего эти счета. Из (4.3) и (4.4) очевидно, что

(4-5)

П р и м е р 4.1. Пусть вкладчик в начале года открывает в первом банке накопительный вклад с начальной суммой .#1000 и ставкой 10\% годовых, а в конце года во втором банке вклад с начальной суммой ,#2000 и ставкой 15\% годовых. Какую сумму накопит вкладчик через полгода? К концу 2-го года?

Решение. В данном случае имеем мультисчет, состоящий из двух субсчетов. Выбирая за начало отсчета начало 1-го года, в соответствии с (4.3) получим систему уравнений:

для динамики мультисчета:

5,(,)= 1000(1+ 0,1/)(^),

S]1] =2000(l +0,15(г-1))(.^) 1^=0,

Г>0; /<0; Г>1;

/<1;

для полного счета:

5,=0,

< 1000(1+0,1/)(Л?),

S, = 1000(1 + 0,1 г) + 2000(l +0,15(/-1 ))(.#), Таким образом, к концу полугодия полный счет составит

г<0;

0</<1;

г>1.

Sni = 1000(1 + 0,1 • 0,5) 1050(.#),

а к концу 2-го года

S2 1000(1 + 0,1-2) + 2000(1 + 0,15-1) = 1200 + 2300 = 3500( Ж).

Понятие полного счета позволяет обобщить на случай финансового потока определенную выше для отдельных событий операцию приведения, связанную с капитализацией и дисконтированием и соответствующими им операторами будущего и текущего значений.

Рассмотрим поток финансовых событий

Cf = {(/1,C1),(«2,C1),...,(/„C.)}

и вектор процентных ставок / = (/,, /2,/я).

Пусть т> ґ, tn — момент приведения, будущий по отношению ко всем критическим моментам потока.

Будущим (накопленным к моменту т) значением мультисчета назовем полное значение Sr (полную сумму) мультисчета в этот момент времени. Будущее значение мультисчета, порожденного потоком CF, обозначим символом FV^{CF). Согласно (4.5) можно записать

FV^iCF^FV^

где FV(C.) — будущее (накопленное) значение в момент т субсчета с начальным состоянием (tk, Ck).

Заметим, что определение будущего значения зависит от вектора і процентных ставок. Следовательно, строго говоря, оператор будущего

значения должен записываться в виде FVX (CF, і).

В частности, когда все ставки одинаковы, говорят о будущем значении относительно этой ставки. Именно этот случай и рассматривается наиболее часто. Будущее значение мультисчета, порожденного потоком CF, совпадает со стандартным будущим значением этого потока в схеме простых процентов (см. § 3.4):

FVrmu]x (CF) = FVT(CF).

Смысл описанной выше операции достаточно очевиден. Он полностью характеризуется понятием полной суммы мультисчета и означает замену распределенных по времени сумм единственной, финансово-эквивалентной им суммой, относящейся к некоторому будущему моменту времени т.

Наконец, используя определенный в предыдущей главе общий оператор текущего значения, можно определить текущее значение мультисчета, порожденного потоком CF, формулой

PVrCF) = ±PVx{CkJk).

Отметим, что момент приведения г в принципе произволен, т.е. может как предшествовать моменту f, к которому относится сумма С, из потока CF, так и следовать за ним.

Как мы помним,

СДі + 'Д*-'*))» еслит>/,; Ск

——- если т < tk.

Таким образом, если момент приведения т удовлетворяет условию

г, <ґ2 <...</, <т</А+1<...<ґя,

то

/>кГ(с,)=|сД,+/Л,-0))+||Т-|^. (,6)

Чаще всего (4.6) используется для момента приведения т, предшествующего всем моментам событий потока. В этом случае

PVr{CF)=± С* (4.7)

*=i l + lkVk ~т)

Это значение часто называют дисконтированным значением денежного потока CF.

В случае совпадения ставок іг — /2 = ... — / = /, как и для будущего значения, текущее значение мультисчета, порожденного потоком CF, совпадает со стандартным текущим значением этого потока в схеме простых процентов:

PV™h(CF) = PVr(CF).

Такая операция дисконтирования используется, в частности, для нахождения текущей стоимости портфеля долговых обязательств, например облигаций, векселей и т.д. Так, с ее помощью решается задача о сумме инвестиций, необходимых для обеспечения потока платежей, порождаемого выплатами номинала облигаций, погашаемых в моменты tk потока.

Пример 4.2. Пусть на рынке имеются два типа облигаций с номиналом .-#1000 и погашением в точности через год и через два года. Предположим, что инвестор желает обеспечить себе поток доходов в j?3000 в конце 1-го и .#5000 в конце 2-го годов. Какую сумму должен вложить инвестор в портфель облигаций, если ставка 10\% годовых (для любого срока)?

Решение. Искомый портфель состоит из трех годовых и пяти двухлетних облигаций и дисконтированная (т.е. приведенная к начальному моменту) стоимость портфеля

ру _ 3000 + 5000 = 2727,27 + 4166,67 = 6893,94р?).

0 1 + 0,1-1 1+0,1-2 v '

Интерпретация общего вида приведения (4.6) более трудна. Формально, как и частные случаи будущего и дисконтированного значений, общее выражение позволяет заменить поток событий (платежей) одним «эквивалентным» событием (суммой) относительно заданного семейства ставок (или одной ставки).

Содержательный смысл как самой операции, так и замещающего поток события неочевиден. Однако такое приведение часто используется при так называемой реструктуризации кредитных контрактов. Более подробно об этом будет сказано при обсуждении схем погашения долга. Сейчас отметим лишь факт наличия некоторой формально корректной процедуры приведения финансовых потоков, описываемой обобщенным оператором Текущего значения. С математической точки зрения этот оператор есть линейный оператор на классе денежных потоков, т.е. для него должны выполняться следующие легко проверяемые свойства:

РУГ]Х (CFl +CF2) = PVTmat (CF,) + PVrmu]x (CF2) (4.8)

и

РУ"Ш]{ (aCF) = aPVrmu]x {CF), (4.9)

где a — любое действительное число.

Использование векторной структуры в модели мультисчета подразумевает #зяшіш>>/о независимость субсчетов. Суммирование состояний этих счетов при определении обобщенной, интегральной характеристики мультисчета и соответствующей ей операции приведения (капитализации и дисконтирования) — лишь один из способов перехода от анализа отдельных событий (сумм) к их потокам. Такой подход уместен, когда описываемые сделки и вместе с ними и участвующие в них суммы не связаны между собой, как это есть, например, в случае портфеля долговых активов (облигаций, вкладов и т.д.). Однако на практике нередко встречаются случаи, когда такой независимости нет. Например, когда в рамках одной-единственной сделки рассматриваются сразу несколько сумм.

В § 1.5 оператор приведения РУТ, полученный линейным продолжением, т.е. простым суммированием текущих стоимостей отдельных событий, для моделей, в которых отсутствует «независимость» отдельных сумм потоков, назван формальным оператором приведения. Таким образом, для таких моделей термины «стандартный» и «формальный» являются синонимами.