12.4. непрерывные ренты

12.4. непрерывные ренты

Непрерывные ренты как пределы /7-кратных рент. В § 12,2 получены формулы для стоимостей /ь кратных обыкновенных рент:

s^=JFfyi (12.71)

и

41=ф)аЯг (12.72)

где i{p) — номинальная /7-кратно начисляемая процентная ставка, эквивалентная нормированной ставке /. Напомним также, что в этих формулах речь идет о единичных/э-кратных рентах, т.е. рентах, для которых сумма всех рентных платежей за единичный (базовый) период времени равна 1. Иными словами, величина каждого отдельного платежа за период ренты h = /р равна также /р. В § 8.4 рассмотрены модели накопления с непрерывным (бесконечнократным) начислением, которые получались с помощью предельного перехода /? —» 0 или р —» «з. В такой модели роль ставки накопления, т.е. основного параметра, определяющего динамику роста капитала, играет номинальная непрерывно начисляемая ставка j = /(со). При этом эффективная нормированная ставка / = /' эквивалентная ставке у, равняется

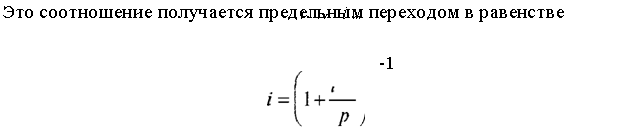
при р —> оо для множества /7-кратно начисляемых ставок, для которого значения соответствующих номинальных ставок равны j: iip) =j.

Осуществляя предельный переход в (12.71) и (12.72) при р-^ оо, получим формулы для стоимостей так называемых непрерывных рент:

с<->

= 151^ = ls2i (12.73)

И

Отметим два момента, связанных с этим предельным переходом. Во-первых, срок ренты п задан в исходной временнбй шкале (например, в годах). Во-вторых, номинальные ставки і(р) эквивалентны заданной нормированной ставке /, т.е.

і^=р[( + і)Ур-\].

В-третьих, несмотря на то, что периоды h — /р и отдельные платежи /7-кратной ренты стремятся к нулю, так как /р —> О, общая сумма платежей за единицу времени равна 1. Учитывая, что

ап-vn

s = и а

где а и v — нормированные коэффициенты роста и дисконтирования, формулы (12.73) и (12.74) можно переписать в виде

4=— (12.75)

и

4/= — • (12.76)

Напомним, что непрерывно начисляемая ставка/ есть не что иное, как интенсивность роста или сила процентов 5, о которой говорилось в гл. 9.

Непрерывные ренты, задаваемые непрерывными потоками. Выше мы получили выражения для стоимостей непрерывных рент в результате предельного перехода в выражениях для стоимостей /г-кратных рент при р—>°°, В этом случае непрерывная рента рассматривается как предел своих дискретных приближений. С другой стороны, можно считать непрерывную ренту частным случаем непрерывного потока CF, задаваемого плотностью pi(t). Тогда условие постоянства платежей С = const за единичный период можно трактовать как стационарность потока, представляющего ренту, или, что то же самое, как постоянство плотности }x(t) = д — const. Напомним, что непрерывный поток платежей задается аддитивной функцией временных промежутков (в заданной временнбй шкале)

Постоянная плотность потока означает просто, что

где х — значение плотности.

Единичная непрерывная рента есть рента с плотностью, равной 1, т.е. fj = 1. Строго говоря, для срочной ренты со сроком п равенство (12.76) справедливо лишь для значений tv t2 из периода (носителя) [г0, г0 + я], в котором сосредоточена рента.

Если через S{t) обозначить накопленную к моменту г стоимость всех платежей непрерывной ренты с плотностью j.i за период от [0, t], то S(t) удовлетворяет дифференциальному уравнению (10.20):

dS(t)

= 6S(t) + fi.

dt

Здесь S — постоянная интенсивность роста, эквивалентная нормированной ставке /; ц — постоянная плотность непрерывной ренты, сосредоточенной на [0, п.

Учитывая, что £(0) = 0, получим решение этого уравнения в виде (см. (10.22))

и поскольку

Gs' = a!,

то получаем еще одно выражение для S(t):

S(t) = ^ 0<t<n. (12.77)

5

В частности, для единичной непрерывной ренты со сроком п получим

т.е. получили тот же результат, что и выше в формуле (12.75), поскольку j S. В литературе по финансовой и актуарной математике накопленную и текущую стоимости единичной непрерывной ренты сроком п обозначают соответственно 1д и Ад. Таким образом, окончательно имеем (12-78)

и

_ 1-и"

где а = 1 + /' = е5 и v = а~{ = е-5.

Уместно отметить, что предельный переход/>—><>=>, с помощью которого нашли стоимость непрерывной ренты, «стирает» различие между обыкновенной и авансированной рентами. Так, если бы в качестве отправных использовались стоимости/?-кратных авансированных рент

и а^}, результат был бы, очевидно, тем же.

Пример 12.23. Найти накопленную и текущую стоимости непрерывной 10-летней ренты, годовые выплаты по которой составляют .-#600. Проценты на платежи начисляются по ставке 10\% годовых.

Решение. Согласно условию и = 600(.3?/год); / = 0,1; п = 10. Следовательно, интенсивность роста (сила процентов)

5=1п(1 + 0,1) 0,0953.

600їш 600^ 1 = 10032,98(#),

Тогда накопленная стоимость составит

0,953

а текущая стоимость равна

600^g =600Х п^ 1 =3868,15(л).

(ИиҐ)

0,953

Устремляя в (12.79) срок ак«, получим стоимость непрерывной единичной бессрочной ренты:

_ 1

Монотонные непрерывные ренты. Используя методы анализа непрерывных моделей накопления из гл. 10, нетрудно получить стоимости непрерывных монотонных рент, являющихся непрерывными аналогами дискретных монотонных рент. Так, единичной арифметической непрерывной рентой называется рента, плотность которой меняется линейно со временем:

МО =

Накопленная за период [0, п] стоимость такой ренты обозначается ~js^, соответственно ее текущая стоимость обозначается . Тогда для текущей стоимости непрерывной монотонной арифметической ренты на периоде [0, п] имеем равенство

Ш ^ tStdt.

о

Интегрируя по частям, получим

" л -St " 1 п п п і

— г _St. -/е 1 г _StJ ~nv V 1

Ш = /е й'с1/-—— + е Stdt = т + -7 =

о

_1-рл пи" _\%-™п

Итак,

а-, —пи"

_ __л)

Поскольку

Is2 =(1 + /)л Ш,

то

— 5-і Л

ism=-л

8

Таким образом, структура формул для стоимостей единичных арифметических непрерывных рент аналогична формулам (12.50), (12.51)

стоимости единичных арифметических дискретных рент с той лишь

разницей, что в них вместо и / используются их непрерывные

аналоги a'-1,J-1 и 8.

Замечание. Стоимости Ш и 1а2 (выражения с двумя надчеркиваниями над 1а и Is) непрерывных рент следует отличать от стоимостей /1^ или Ia-^ (выражения с одним надчеркиванием). Последние два выражения относятся к так называемым дискретно-монотонным непрерывным рентам, т.е. рентам, у которых плотность является кусочно-постоянной функцией:

если0<г<1;

если2</<2;

п, если n-\<t<n.

Стоимость такой ренты можно получить, преобразовав ее в эквивалентную дискретную монотонную (арифметическую) ренту, с помощью замены непрерывных платежей, в пределах каждого промежутка постоянства, на их приведенную к концу этого промежутка стоимость. Тогда часть ренты, относящаяся к периоду [k—l, к], имеющая на нем плотность ку заменяется на накопленную к моменту к стоимость, равную согласно (12.78) для п — 1 _к(а-)_ Щ 1,1 8 8

Тогда исходная рента преобразуется в арифметическую ренту (і/8)Ап с платежами

С -— к2 п д

Накопленная стоимость такой ренты равна, очевидно, (//8) кш. Таким образом,

і s^-n 8 5

и

Полученные формулы отличаются от своих дискретных аналогов (12.50), (12.51) только знаменателем, в котором вместо ставки/стоит ее непрерывный аналог интенсивность 8.

Ренты с дробными сроками. В заключение этой главы коснемся одного достаточно тонкого вопроса, связанного с рентами.

Во всех формулах, связанных с дискретными рентами, срок л ренты являлся целочисленно кратным периоду ренты Л:

n = kh, к є N.

Здесь срок и период ренты задаются в исходной временнбй шкале.

Принимая в качестве единичного периода период ренты, получим, что п должно быть целым числом. Тем не менее сами выражения для стоимостей рент всех видов определены для любых значений параметров п, іуру 8 и т.д., входящих в область определения этих выражений, в том числе и нецелых значений п. Это обстоятельство использовано при выводе специальных формул стоимости рент. Однако лишь в случае непрерывных рент значения sT]na7] имеют прямой содержательный смысл для произвольного t> 0, определяемый моделью накопительного фонда (см. (10.23)). Тем не менее во многих практических задачах, в которых требуется нахождение срока ренты (или числа платежей), последний находится, например, как решение уравнения

а, А или s В

при известных А, В, Ї, 8 и т.д., но неизвестном п. Решение таких уравнений может приводить к нецелым значениям п. В этом случае в качестве решения задачи берется одно из ближайших целых значений т и т + 1, между которыми лежит полученное значение п:

т < п < т + 1.

При этом выбор т в качестве окончательного решения означает изменение (увеличение) последнего (т-го) платежа ренты на величину (поправку), приводящую к точному стоимостному балансу.

Соответственно, выбор в качестве ответа т+ означает, что эта поправка выплачивается отдельно в качестве дополнительного платежа. Текущая величина поправки легко находится из исходного уравнения для п. Например, если п находится из уравнения

а-Л~ А

1

при известной ставке /, то, полагая

я = т + Д 0</3<1,

получим или

= л.

Последнее уравнение можно переписать в виде или

Смысл этой формулы прост. Исходная рента со стоимостью Л, срок которой требовалось найти, состоит из обычной ренты с теми же параметрами и целочисленным сроком и дополнительного платежа (поправки), текущая стоимость которого (в момент t—Q)

-v0

PV0(C') = A-a^=v"

і

Если этот платеж осуществляется в момент т, то поправка равна

с =—=«,,,

где 0 < (3 < 1, если же дополнительный платеж относится на момент т + 1, то

c=(i+')v

Пример 12.24. Участник пенсионной схемы к моменту выхода на пенсию имеет на своем пенсионном счете .#50 ООО. Согласно пенсионному договору участник получает с момента выхода на пенсию ежемесячную пенсию в ,#500. Сколько пенсионных выплат получит участник схемы и какова их общая сумма, если ставка накопления фонда 10\% годовых.

Решение. Выберем в качестве базовой единицы временнбй шкалы месяц. Тогда срок ренты будет задан в месяцах. Месячная ставка г, эквивалентная ставке накопления фонда,

г = іф2 = (1 + 0,1)'/121 = 0,00797.

Таким образом, пенсионная рента является ежемесячной рентой стоимостью в ,#50 000, ежемесячными платежами по ."#500 и месячной ставкой /• = 0,797\%. Уравнение для текущей стоимости такой ренты имеет вид

500о^г =50000,

1-а"

те а-, =100 или = 100,

где v — 1/(1 + г).

Решая это уравнение, получим

п = -^ = 201,1223.

In(L+r)

Таким образом, в данном случае

m = 201 (мес); Р= 0,1223(мес).

Пусть поправка выплачивается в конце 201 месяца. Тогда она равна

С' = 500вдг=6О,88(;#).

Следовательно, участник схемы получит 200 ежемесячных платежей по .#500 и последний 201 платеж .#560,88. Общая сумма выплат составит

500-200 + 560,88 = 100560,88( .#).

Если бы поправка выплачивалась дополнительным (отдельным) платежом, то она была бы равна

(1 + r)c= (1 + 0,00797)60,88 61,36(.#).

Вопросы и упражнения

Опишите основные типы рент и их параметры.

Выпишите формулы для накопленной и текущей стоимостей простой (стандартной) ренты.

Сформулируйте два подхода к сведению общих рент к простым (стандартным) рентам: а) метод эквивалентных преобразований; б) метод эквивалентной ставки.

Получите из формул стоимостей стандартных рент с нормированной ставкой выражения для стоимостей рент с использованием: а) ставки начисления ih; б) ставки дисконтирования dh; в) номинальной ставки г) номинальной ставки d[m) д) номинальной ставки j = /(~

Выразите формулы стоимостей стандартных рент в терминах постоянной силы процентов 8.

Выразите формулы стоимостей рент с произвольным периодом h в терминах постоянной силы процентов 8.

Выпишите формулу стоимости непрерывной ренты с постоянной плотностью.

Задачи

Найти текущую и накопленную стоимости 20-летней обыкновенной ренты с ежегодными платежами :#500 в конце каждого года при ставке 20\% годовых, начисляемых раз в квартал. s

Текущая стоимость обыкновенной ренты с ежегодными платежами при ставке 20\% годовых равна S1000. Какова будет текущая стоимость такой ренты, если платежи (при той же их величине) будут выплачиваться раз в полгода?

Найти х из уравнения

a^{+v*W«) = a2r

Пусть яд,. =х и а^ = у. Выразите ставку / как функцию от х и у.

Стоимость обыкновенной единичной вечной ренты равна $20. Найти стоимость отложенной на 5 лет единичной авансированной вечной ренты.

Найти текущую стоимость 5-летней обыкновенной ренты с ежеквартальными платежами по к руб. в к-м году (к = 1, 2,..., 5), если ставка ренты составляет 16\% годовых, начисляемых ежеквартально.

7. Докажите, что

■~ап = 1 + 8а7].

8. Докажите справедливость разложения

я «~л л{л-1)(й-2) ,

ая =п+— -/+— -г +

2! 3!

20

9. Упростите выражение ^jT ^.

я=10