3.2. накопительные модели в схеме простых процентов: динамическая модель роста

3.2. накопительные модели в схеме простых процентов: динамическая модель роста

Одним из наиболее распространенных применений простых процентов являются так называемые накопительные, или сберегательные счета. Они относятся к более широкому классу счетов, вкладов или депозитов до востребования и, следовательно, не имеют определенного срока. Таким образом, вкладчик может изъять весь вклад или его часть в любое время. За эту возможность (или, как говорят, опцион) вкладчик платит снижением процентной ставки по сравнению со срочным депозитом, т.е. вкладом на конкретный срок.

Хотя внешне накопительный вклад определяется как один контракт, т.е. как одна сделка, с формальной точки зрения ее можно рассматривать как потенциальный простой класс из бесконечного числа простых сделок. Пусть вкладчик открывает счет в момент времени /0 с начальной суммой S, . Тогда любому t > 0, учитывая возможность изъятия вклада в этот момент времени, соответствует некоторая потенциально возможная срочная сделка с периодом [ґ0, t].

Естественно, с течением времени сумма вклада растет, так что к моменту времени / состояние счета описывается величиной (суммой) St. Если / — процентная, например годовая, ставка по вкладу и время также измеряется «в годах», то динамика накопления описывается уравнением

Sl=Sto( + i(t-t1ij) = SlX + iT) (3.3)

или

St=Sta{tatt), (3.4)

где

a(tQj) = +i(t-t0) = +iT (3.5)

— коэффициент роста (наращения); Т= t — tQ — срок в годах.

Уравнение (3.3) обычно трактуется как динамическая модель роста накопительного счета в отличие от уравнения (3.2), описывающего различные сделки, например осуществляемые одним банком с разными вкладчиками. В модели (3.3) время Т теоретически принимает любые неотрицательные вещественные значения, тогда как в модели (3.2) семейство сроков |jT| се С} сделок зависит от рассматриваемого класса сделок.

Конечно, на практике это различие не стоит абсолютизировать. Так, даже для срочной сделки со сроком Г кредитор (например, вкладчик) может досрочно расторгнуть сделку, так что реальная длительность сделки может быть меньше, чем 7 Возникает вопрос о величине возвращаемой суммы долга для этих условий. И в этом случае часто используется динамическая модель типа той, что была рассмотрена выше.

Наконец, динамическая (накопительная) модель используется для определения так называемых накопленных процентов в сделках с упоминавшимися выше процентными бумагами, такими, как депозитные сертификаты, облигации и др. (см. гл. 2). Процентные бумаги имеют в качестве обязательных реквизитов номинальную стоимость (номинал) и процентную ставку, называемую в этом случае купонной. Выплата процентов или, как еще говорят, купонного платежа осуществляется эмитентом ценной бумаги во вполне определенные моменты времени, например для депозитного сертификата — это момент погашения, а для облигации — концы так называемых купонных периодов. Такие платежи можно рассматривать как выплату процентов по простой кредитной сделке с начальной суммой долга, равной номиналу ценной бумаги, и сроком, равным длине купонного периода. В этом случае говорят о выплате полного купона. Если же ценная бумага продается до погашения между купонными выплатами, то в цене продажи учитываются накопленные (по купонной ставке за период от последнего купонного платежа до момента продажи) проценты к номиналу ценной бумаги. Таким образом, покупатель ценной бумаги выплачивает продавцу, кроме номинальной стоимости ценной бумаги, накопленные проценты (неполный купон). Покупатель вернет эту сумму (накопленные проценты) при очередной выплате купонов.

Заметим, что к счетам до востребования кроме накопительных счетов относятся также так называемые расчетные или текущие счета фирм и частных лиц. В отличие от накопительных счетов их цель состоит в осуществлении текущей деятельности, в постоянно возникающих расчетах, оплате товаров, услуг и т.п. Эти счета доступны в любое время как для перечисления, так и для снятия средств. Как правило.

проценты по этим счетам не начисляются. Однако следует сказать, что в последнее время многие финансовые учреждения Запада открывают для своих клиентов счета, позволяющие объединить накопительную и расчетную функции. Это относится и ко многим отечественным банкам. Правда, при этом требуется поддержание определенного минимума остатка средств на счете и, конечно, ставка по таким счетам намного ниже, чем по сберегательным.

Наконец, отметим, что классический срочный вклад (срочный депозит) является примером простой кредитной сделки с заранее определенным сроком. Таким образом, теория простых процентов изучает все многообразие различных видов краткосрочных кредитных операций (сделок).

Вернемся снова к формуле (3.3), описывающей динамику накопления. Заметим, что эта формула была получена в предположении, что период, по отношению к которому указывалась процентная ставка, т.е. — период начисления совпадает с единицей времени, например задается годовая процентная ставка и время измеряется «в годах». Снимем теперь это ограничение и рассмотрим более общий случай.

С формальной точки зрения накопительная модель или модель накопительного счета описывается следующим образом. Во-первых, фиксируется временная шкала Т. Во-вторых, задается так называемая ставка начисления, характеризующая динамику роста накопительного счета. Ставка начисления включает указание периода начисления h и числового значения ставки за этот период. Таким образом, в математическом плане ставка начисления представляет собой пару (h, і). Для того чтобы подчеркнуть привязку числового значения ставки / к конкретному периоду И, в формулах это значение записывается в виде ih. Такое индексное обозначение содержит упоминание как о величине ставки, так и о ее периоде, и потому мы будем использовать его наравне с каноническим обозначением в виде пары (/г, /). Наконец, последним элементом формального описания модели накопительного счета является уравнение динамики счета

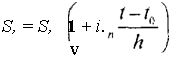
(3.6)

Заметим, что здесь все временные характеристики заданы в выбранной временной шкале. В частности, h есть длина периода начисления относительно единичного (базового) периода временной шкалы. Тогда величина h~ h

будет равна продолжительности накопления в единицах периода начисления. В случае, если период начисления будет совпадать с единичным периодом временной шкалы, то h = 1 и (3.6) примет вид (3.3). Заметим, что формулой (3.3) можно пользоваться и в общем случае, если определим нормированную ставку начисления как ставку, относящуюся к единичному периоду временной шкалы и равную

i = . (3.7)

п

Определение нормированной ставки начисления вполне аналогично определению нормированной ставки сделки из предыдущей главы. Задание ставки начисления на практике обычно сопровождается явным указанием периода начисления, к которому она относится. Так, говорят о 10\% в год, или 10\% годовых, 5\% в месяц и т.д. Соответствующая нормированная ставка также сопровождается указанием единичного периода, к которому она относится. Если шкала годовая, то нормированная ставка будет годовой.

Рассмотрим пример накопительного счета.

П р и м е р 3.1. Вкладчик открывает накопительный счет с начальной суммой .#500, и пусть для простоты t0 — 0, Годовая процентная ставка равна 12\%. Какова величина счета: через месяц, год, два года, десять лет?

Решение. Ставка начисления, по условию, задана как годовая. Проще всего в этом случае в качестве временной шкалы взять годовую шкалу. Тогда, используя уравнение (3.3), получим величину вклада:

через месяц

S1/I2 =500^1 + 0,12-~j = 505(.*');

год

5, = 500(1 + 0,12) = 560( ;■'#);

два года

S2 = 500(1 + 0,12-2) = 620(.J?);

10 лет

£„, = 500(1 + 0,12-10) = 1100(.#).

Заметим, что тот же результат получили бы в примере 3.1, если бы в качестве ставки начисления была задана месячная ставка 1\%. В этом случае для годовой шкалы соответствующая нормированная годовая ставка будет равна 12\%. Очевидно, что результат накопления по 12\%-ной

S Sh ~ S0

1 •h)

В этом случае нормированная ставка начисления совпадает с нормированной ставкой сделки. Более того, если, как сказано выше, накопительную модель интерпретировать статически как семейство {ch, h>0) простых сделок ch (см. гл. 2), то они составляют простой класс сделок с общей нормированной ставкой /, которая является процентной ставкой класса. Поэтому в дальнейшем при описании накопительных моделей в качестве ставки, определяющей динамику роста счета, будем использовать, как правило, нормированную ставку.

Пример 3.2. Найти месячную ставку, эквивалентную простой годовой ставке, равной 10\%.

Решение. Обозначим месячную ставку через / что соответствует ставке для 1/12 года. Вкладывая, например, S1 на 1 год под 10\% годовых, имеем, что

1 +0,1 1,1(5).

С другой стороны, эта финансовая операция, если базовая единица времени есть 1 мес, равносильна инвестированию S1 на 12 мес. по ставке / р. Тогда наращенная сумма составит І + 12/. Так как имеем одну и ту же финансовую операцию, то наращенные значения в обоих случаях совпадают, поэтому

1+0,1 = 1 + 12/,. р_,

или

0,1 = 12/1/1Г

Отсюда следует, что

или 0,83\% месячных.

В модели накопительного счета особенно легко интерпретируется понятие накопленного (наращенного) значения и соответствующего оператора FVr В силу самого смысла накопительного счета его состояние St в момент времени t представляет собой результат накопления за счет начисления процентов на вклад за период времени [г0, г]. Таким образом, смысл равенства

FV,{s„) = S,=S,a{tt,l), (3.8)

где коэффициент роста a(t і) определяется формулой (3.5), становится очевидным. Важно, что это равенство определено для всех / > tQi т.е. о величине или состоянии счета можно говорить в любой момент времени, следующий за начальным.

Заметим, что в аналогичных (3.8) по смыслу равенствах (2.2) и (2.3) наращенное значение S 1+Т было определено лишь для конца t{~ tti + Т периода [/0, /. J сделки. Для внутренних точек этого периода, т.е. для /0 < t < < t, значение St без предварительных соглашений определить нельзя. Здесь требуется введение дополнительных уточнений в модель. Необходимость такого рода уточнений может возникнуть, например, при досрочном расторжении сделки. В этом случае необходимо найти величину суммы долга, которую должен вернуть должник кредитору.

Рассмотрим накопительную модель, задаваемую (3.3) (3.5) и (3.8), более подробно.

Уравнение (3.8) является формальным выражением динамики (роста) накопительного счета. Линейный вид коэффициента роста fl(f0,f) = l + l(/-/0), t>t0

указывает на конкретный вид этого закона в схеме простых процентов. Коэффициент роста инвариантен относительно сдвига на любой период И:

a(t0 + h,t + h) = a(tQ, /).

Эта инвариантность обусловлена тем, что коэффициент роста зависит, по существу, не от моментов времени г0, ґ, а от расстояния T~t—t0 между ними, т.е. от длины промежутка [/0, /]:

а(^) = а(г-^) = аТ.

1

Здесь

аТ~ і +iT

— стандартный (одномерный) коэффициент роста. Хотя общий (двумерный) a(tQ, t) и стандартный (одномерный) аТ коэффициенты — безусловно различные объекты, так как первый является функцией двух, а второй — функцией одной переменных, мы обозначим их одной и той же буквой а в тех случаях, когда это не будет приводить к недоразумениям.

Таким образом,

fl(r0,/) = l + i(r-r0) = l + /r = flr (3.9)

St=S,a(t0it) = S,aT. (3.10)

В дальнейшем для простоты начальный момент сделки /0 будет часто отождествляться с началом временной шкалы, т.е. будет полагаться Г0 = 0. В этом случае формулы (3.9) и (3.10) примут простой вид

a(0,t)= l + it = at (3.11)

и

St=SQat. (3.12)

Вернемся теперь к соотношению (3.3) или, что то же самое, к уравнению (3.10), описывающим динамику накопительного счета, и покажем, что процентная ставка / задает его относительную скорость роста.

В самом деле, полагая в (3.12) 50 = 1, получим

Из (3.11) немедленно следует, что da,

—і.

dt

Таким образом, процентная ставка і действительно определяет скорость роста единицы вклада или, что то же самое, относительную скорость роста вклада (по отношению к начальной величине).

Выше дана еще одна интерпретация нормированной процентной ставки дополнительно к двум ее толкованиям, приведенным в § 2.2. Следовательно, подводя итог, можно сказать, что нормированная процентная ставка имеет три важнейшие интерпретации. Во-первых, она определяет (для должника) стоимость кредитных ресурсов на кредитном рынке. Во-вторых, для кредитора она характеризует доходность (эффективность) использования свободных (или привлеченных) средств. Наконец, в-третьих, в накопительных моделях она характеризует относительную скорость роста счета (вклада).

Пример 3.3. Сумма У>?1000 вкладывается в момент времени гн = 0 под 10\% годовых: а) на 2 года; 6) 1 год, по истечении которого наращенная сумма вкладывается (реинвестируется) еще на 1 год. Найти для обоих случаев наращенную сумму S, на конец 2-го юла.

Решение. В первом случае, согласно формуле (3.3), наращенная сумма за 2 года

52 = 1000(1 + 0,1-2) = 1200 (.'*). Во втором случае наращенная сумма за 1-й год

5, = 1000(1 + 0,1-1) = ]00иЩ.

Теперь, если сумма S вкладывается еще на 1 год под те же 10\% годовых, то по истечении 2-го года получим сумму

S2= 1100(1 + 0,1-1) = 1210(.-Я),

т.е. во втором случае, когда после 1-го года наращенная сумма была реинвестирована, получили сумму S„ накопленную за 2 года, равную :#1210, что не совпадаете результатом S2 = 1200 для первого случая.

В заключение кратко остановимся на геометрической интерпретации, отражающей движение во времени накопительного счета.

Динамику накопительного счета можно наглядно изображать соответствующей траекторией на фазовой плоскости время деньги. В силу линейности закона накопления такая траектория будет представлять собой луч с вершиной (?0, S0) и угловым коэффициентом iS0, где (/0, SQ) ~~ начальное состояние счета (рис. 3.1). Пожалуй, самым существенным свойством процесса накопления в схеме простых процентов — это его в некотором смысле абсолютная привязанность к начальному состоянию. Как увидим ниже, траектории двух процессов с разными начальными состояниями не могут иметь общего продолжения, ни даже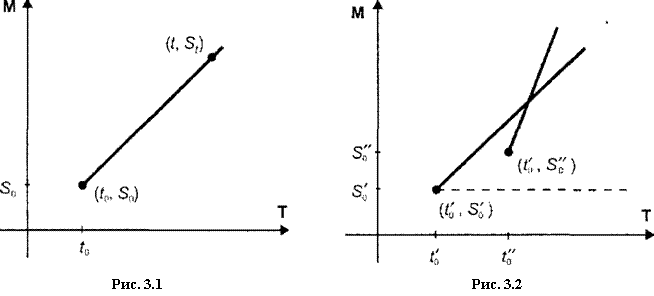

общего участка траектории. Они могут лишь пересекаться в одной-единственной точке. Таким образом, процесс накопления в схеме простых процентов всегда «помнит свой день рождения».

Заметим, что два состояния (f{, S{) и (tv S2) процесса, порождаемого данным вкладом, в свою очередь, будут порождаться начальным состоянием (r0, SQ) и, следовательно, будут лежать на одной траектории, если

^ = ^(1 +!(/,-/„)); S2 = SQ(+i(t2-t0)),

откуда следует

l + /(Wo) 1 + '(/2-О" Отметим также, что вклады с одной и той же ставкой /, но разными начальными состояниями (t'0,5J)и(/0",могут иметь пересекающиеся траектории. Пересечение будет иметь место, если уравнение

50'(l + l(r-/0')) = 5;(l+/(f-r0"))

имеет решение t > ?0', г0".

Легко доказать, что при заданном начальном состоянии (^0',50')

любое другое начальное состояние лежащее внутри сектора,

ограниченного траекторией с начальным состоянием (t^S^) и горизонтальным лучом S = Sq, порождает траекторию {рис. 3.2), пересекающую траекторию с начальным состоянием (ґ0', £0').

Пример 3.4. Пусть счет с начальной суммой .#100 при головой ставке 20\% открывается в момент времени t'{) =0. Спустя год открывается счет с начальной суммой .#110 и с той же ставкой. Найти момент времени, когда накопленные суммы на обоих счетах сравняются.

Решение. Динамика этих счетов описывается уравнением для первого

S, = 100(1 + 0,2/) = 100 + 20/, / > 0

и второго вкладов:

5, =110(1+ 0,2(/-1))= 88 + 22/, г>1.

Накопления на обоих счетах совпадут в момент /, определяемый уравнением

100 ■+ 20/ = 88 + 22г,

откуда следует, что / = 6.