7.2. дискретная модель в схеме простых процентов с переменной ставкой

7.2. дискретная модель в схеме простых процентов с переменной ставкой

Модель с постоянным капиталом. Начнем с анализа динамики процентного роста одной суммы. Рассмотрим произвольный промежуток времени [tQ, ta + 7] и начальную сумму S, . Пусть указана последовательность моментов tk, к — 1, 2,...,«— 1 из промежутка [tQ, tQ + 71 таких, что

L<t.<L<...<t <t+T=t, разбивающая промежуток [tQ, tn] на промежутки [tkV tk] длины

hk = tk~fk-i> £=1,2,...,/?. Тогда исходный промежуток [tQ, t0+T представляется в виде объединения

M+^ = UlW*]к=

Концы полученных промежутков разбиения, т.е. точки деления, назовем критическими моментами.

Далее, пусть для каждого промежутка [tkl, tk] задана своя, действующая на этом промежутке, нормированная ставка ik> соответствующая единичному базовому периоду. Другими словами, на промежутке [/0, / J имеем ставку /, на промежутке [/, f ] — ставку / , и, наконец, на последнем промежутке [ґ , / ] ставка равна /

Покажем, что для наращенной суммы 5^ к концу tn = t0 + Т последнего промежутка имеет место следующее выражение:

$.=sJi+£vA (7.з)

Докажем формулу (7.3), пользуясь методом математической индукции. При п ~ 1 имеем всего один промежуток [Г0, /J, fj tQ + hx и, следовательно,

т.е. формула (7.3) верна для п = 1.

Предположим теперь, что (7.3) выполнена для некоторого числа m интервалов, 1 < m < п, т.е.

( m

S,.=S, l+IV. ■ (7-4)

Покажем теперь, что (7.3) имеет место также для случая, когда число интервалов равно т + 1.

Так как рассматривается схема простых процентов, то наращение процентов на начальную сумму S, на каждом интервале [tk tk] происходит независимо от наращения на предыдущих интервалах. Следовательно, имеем, что

И

S, =S, +Jm.

'm + I 'm m

Отсюда и из равенств (7.4) и (7.5) получаем, что

Тем самым, формула (7.3) доказана.

В частности, если ставки на всех промежутках, составляющих разбиение промежутка [г0, f0 + Т, одинаковы, т.е.

/, = /' ... і /,

12 m '

то из (7.3) следует, что

5,,i=s;,[i(7.6)

Вспоминая, что tn = tQ + Т, приходим к выводу, что (7.6) есть не что иное, как основная формула простых процентов (3.2), записанная в другой форме.

Заметим, что произведение hjk есть ставка за период [tk_]t tk]

Г* = АЛ>

так что формулу (7.3) можно переписать в виде

s,,=sJl+ln (7-7)

V k= J

Наконец, из определения ставки за период и из последнего равенства следует, что ставка гТ за период tn] есть сумма ставок за все подпериоды [tk[, fj, k = 1, 2,..., п:

4»^.]) = І^.'*]). (7-8)

k=

или коротко

гг=2,гк. (7.8')

Это свойство аддитивности ставки за период будет играть важную роль в последующем изложении.

Пример 7.1. Инвестор вложил в банк .#5000 сроком на 4 года под простые проценты. При этом контрактом предусмотрено, что процентная ставка за 1-й год составляет 10\% годовых, за 2-й — 15\% и за два последних года — 20\%. Какова будет накопленная сумма через 4 года?

Решение. В данном случае промежуток времени в 4 года разбивается па п = 3 интервала. При этом ht = 1 год, А, = 1 год и /?3 = 2 года. Согласно условиям контракта /, = 0,1; /, = 0,15 и Л = 0,2. Тогда, считая, что контракт был заключен в момент времени tu, согласно формуле (7.3), имеем, что накопленная к концу срока сделки сумма равна

Sv4 = 5000( 1 + 0,1 1 + 0,15 1 + 0,2 ■ 2) 8250(.#).

Пример 7.2. Сумма ;К*2000 вложена в банк под простые проценты сроком на 1,5 года на следующих условиях: процентная ставка за 1-й квартал составляет 10\% годовых, за 2-й — 12\%, за два последующих квартала — 15\% и за два последние квартала — 20\% годовых, Найти наращенную сумму по истечении срока вклада, а также процентную ставку за период сделки и соответствующую годовую простую процентную ставку.

Ре пі е н и с. Задачу можно решить либо в исходной годовой шкале, либо переходя к квартальной шкале.

В годовой шкале имеем

Г = 1,5; Л^Л; А3=А4=1. Применяя формулу (7.3), получим

S1S = 2000 Г 1 + --0Л+--0Л2 + --0,15 + --0,2) = 2460Ш.

I 4 4 2 2 ) У '

При выборе квартальной шкалы необходимо найти соответствующие квартальные ставки для заданных годовых ставок. Если / — годовая, а/ — соответствующая квартальная ставка, то / = і/4.

Следовательно, соответствующие квартальные ставки:

0 1 0 12 0 15 0 2 .

у, = — = 0,025; у2=-^ = 0,03; у, = 0,0375; ;4 -0,05.

4 4 4 4

Применяя снова формулу (7.3), получим

Sh = 2000(1 + 1-0,025 + 1-0,03 + 2-0,0375 + 2-0,05) = 2460(.'#).

Процентная ставка за период сделки

2460-2000 460

г = = 0,23, или 23\%.

2000 2000

Тогда нормированная годовая процентная ставка

, = ML о,1533, или 15,33\%. 1,5

Модель с переменным капиталом. Мы изучили модель сделки с переменной ставкой для постоянного капитала. Совершенно аналогично обобщаются на случай переменных ставок модели с переменным капиталом, в частности коммерческая и актуарная и соответствующие им модели обобщенных кредитных сделок. Случай переменных ставок практически автоматически переносится на упомянутые модели. В -этом случае наряду с критическими моментами образующего потока CFнеобходимо рассматривать критические моменты, соответствующие (скачкообразному) изменению процентной ставки. Фактически в качестве исходных параметров модели задаются два потока: поток платежей CF — поток 1-го рода и поток ставок RF (rate flow) — поток 2-го рода

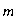Л/7 = {(<71,/1),(<72,/2),...,(а/м,(/

)}•

где о~А — промежуток времени; / — нормированная ставка, действующая на этом промежутке.

Критические промежутки обоих потоков могут не совпадать. Однако можно добиться согласованного представления обоих потоков с одним и тем же множеством критических моментов и промежутков, если допустить нулевые (фиктивные) платежи в потоке платежей и повторяющиеся (совпадающие) ставки в потоке ставок.

Критические моменты для согласованного представления образуются объединением критических моментов обоих потоков, что соответствует измельчению (разбиению) исходных критических промежутков этих потоков. Соответствующие значения платежей и ставок переносятся естественным образом, платеж в новой критической точке (соответствующей изменению ставки) равен нулю, а значение ставки с промежутка переносится на все более мелкие промежутки, образующие измельчение исходного промежутка. Тогда согласованное представление потоков имеет вид

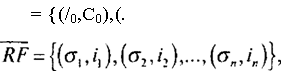где ст. = [г. ,, Л], к~, 2,..., л, — критические промежутки, общие для обоих потоков; СА и /' — платежи и ставки, соответствующие этим промежуткам. Согласно сказанному выше, здесь считается, что если момент tk не является критическим, соответствующим реальному платежу, то Ск = 0, а значение ставки на интервале ок определяется последним, предшествующим моменту tk критическим моментом для ставок.

Теперь легко обобщить рассмотренные в гл. 4 модели с переменным капиталом на случай переменных ставок. В принципе ничего в описании этих моделей не меняется, кроме одного пункта, касающегося вычисления текущих процентов за к-р[ период <тЛ, которые теперь вычисляются по правилу

учитывающему значение ставки ік на промежутке ак; здесь hk=tktk_v В моделях с постоянной ставкой имеем, что ік — / для всех к. В остальном никаких изменений в схемах расчетов для этих моделей нет.

Для коммерческой модели можно выписать рекуррентые формулы для состояния счета в любой критический момент времени:

р = С •

1 0 *"0>

/0=/0=0; Jt = Pt.JAl Л=Л-і+С»; /»=/.

Легко переписать и рекуррентные формулы для актуарной модели. Мы не будем этого делать, а ограничимся примером.

Пример 7.3. Рассмотрим в годовой шкале поток

CF= (0,200),

-1000

,1000

,-2000

Найти состояние счета, порождаемого этим потоком, для коммерческой и актуарной моделей, если начальный уровень процентной ставки 12\% годовых и каждые два месяца он увеличивается на 6\% (в абсолютном смысле).

Решение. В этой задаче критические промежутки для потока CF— кварталы, а для

потока RF — двухмесячные периоды. В годовой шкале поток ставок представится следующим образом:

^ (

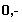
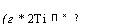= 0,12; і

V (

V

і б'з.

5" 3'6

л)

= 0,18; Л

= 0,36; /

\_

3'2J

0,24;

= 0,42.

В качестве критических моментов для согласованного представления обоих потоков Удобно взять месячные точки:

Тогда для потока платежей Ск = С((к) имеем

С() = 2000; С, = -1000; С6 1000; С9 --2000

иСк0 для остальных к.

Для потока ставок ik = i([{k_r tk]) получим

/, = i2 = 0,12; /3 = /4 =0,18; /5 = /6 = 0,24; /7 = /„ ~ 0,3; /, iw = 0,36; ; = iu = 0,42.

Для коммерческой модели соответствующие вычисления приведены в табл. 7.1, для актуарной модели — табл. 7.2.

Приведенные выше модели относятся к классу динамических моделей. В них изменение ставок осуществляется с течением времени. Такие модели обычно называют моделями с переменной ставкой.

В предыдущих главах показана, что существенные аспекты динамических моделей в стандартной схеме простых процентов (т.е. в схеме с постоянной ставкой) можно изложить, используя абстрактные операции приведения финансовых событий и потоков платежей.

Покажем, что и в случае переменных ставок можно естественным образом определить соответствующие операторы приведения событий и потоков.

Схема простых процентов с дискретной структурой процентных ставок. Выше мы фактически использовали операции приведения событий и потоков к будущим моментам времени. Так, формула (7.3) есть не что иное, как выражение для будущей стоимости начальной суммы St счета. Рекуррентные формулы для динамики счета в коммерческой и актуарной моделях позволяют находить состояния счета в произвольные моменты времени t > ro, что равносильно определению будущей стоимости платежей, составляющих поток, который порождает данный счет.

В предыдущем изложении динамических моделей мы ограничились, во-первых, конечным промежутком, в рамках которого задавалось семейство ставок (т.е. поток RF) и поток платежей, и, кроме того, осуществляли так называемую операцию согласования потока ставок и потока платежей.

Изложим более общий подход, который приведет нас к понятию общей схемы простых процентов. Центральную роль в этом подходе играет дискретная временная структура процентных ставок, задаваемая потоком /^ = {...,(сг_1,/_]),(а0Л),(<тР/1),...}, (7.9)

теоретически бесконечным в обе стороны.

Для заданного потока RF ставок определим ставки (ненормированные)

rk=ikhk, keZ, (7.10)

для каждого критического периода hk — tk — tkV Эти однопериодные ставки можно аддитивно продолжить на произвольные последовательные объединения критических промежутков:

т

Наконец, для любых моментов времени t < т таких, что tk_l<t<tkn t х < < T<tm определим

r(f>Т) = {** 0 '* + 1, * + (т " L-i) '„ • (7.12)

Ставки r(t, т) позволяют определить операции приведения событий в схеме простых процентов с заданной структурой процентных ставок.

Рассмотрим произвольное событие (t, Q. Тогда его будущее значение определяется как

/^(С/) = С,л(г,т) = С,[1 + г(/,т)], т>/. (7.13)

Здесь

fl(f,T) = l+r(f,T), T>t

коэффициент роста.

Операция дисконтирования определяется двойственным образом:

^^Cj = C,rf(/,T) = TT5_, r<t, (7.14)

где 1

7 1 + г(/,т)

коэффициент дисконтирования.

Наконец, используя введенные коэффициенты роста и дисконтирования, можно ввести обобщенный коэффициент приведения

Иг,г), т>/; °М>(г,т). т</. <™>

С помощью обобщенного коэффициента v(tt т) можно определить общий оператор приведения (обобщенный оператор текущей стоимости) событий (денежных сумм) относительно заданной структуры RF процентных ставок;

PVp(C,) = C,v{t,p). (7.16) Строго говоря, следовало бы вместо сокращенного обозначения

PV{Ct) писать PVp(f,C;RF), указывая структуру ставок, относительно

которой осуществляется приведение.

Наконец, операцию приведения событий можно тривиальным образом распространить на произвольный поток

CF-{(t1,Cl),{h,C2),-,(t.,C.)}

с помощью линейного продолжения

PV, (CF) = tPK (с<) = £cA't. Р (7.17)

ы fc=l

Этот оператор приведения является обобщением (формальным) стандартного оператора приведения на случай переменных ставок, заданных структурой потока RF.

Нетрудно показать, что определенные выше операторы играют в обобщенных коммерческой и актуарной моделях ту же роль, что и стандартные операторы в моделях с постоянной ставкой. Так, имеет место аналог теоремы 4.1. Иными словами, в обобщенной коммерческой модели, порождаемой потоком

CF = {(tM(t1,C1),...,{t.,C.)},

для заданной структурой процентных ставок RF справедливо равенство

S,=Frt(CF,)t (7.18)

где St — состояние счета в момент /; CF — начальный отрезок (до момента ї включительно) порождающего потока.