9.2. функции роста

9.2. функции роста

Введем еще одно важное понятие, связанное с характеристикой изменения фондовых величин. Пусть S{t) — некоторая ненулевая фондовая величина, определенная для t>tQn описывающая некоторый процесс роста (накопления) с начальным значением S(tQ) Ф 0.

Величина д(г), t > tQ определяемая как

называется (начальным) множителем наращения или коэффициентом роста. Ясно, что

1.

Его смысл очень простой: он показывает, во сколько раз увеличится величина Sза период [tQ, /]. Так, для накопительного вклада в схеме простых процентов с начальным состоянием (/0, S(t0)) коэффициент роста

a(t)=l+i(t-Q,

а для накопительного вклада в схеме сложных процентов (непрерывная модель)

«(') = (!+'•)""•

Часто вместо коэффициента роста рассматривают более общую функцию роста

й('!,/2)=\%)' /іЛ"'0' (9Л2) характеризующую рост величины Sна отрезке [tp t2].

Отметим, что, говоря о функции роста, мы не требуем, чтобы она была больше единицы при возрастающих моментах времени, т.е. чтобы a(tv t2) > 1 при t{ < t именно тогда функция S(t) будет возрастающей:

. Щ) < S(t2).

Стоимость актива может возрастать, по крайней мере, на это надеется инвестор. Однако она может и уменьшаться. В последнем случае S(t) — убывающая функция времени и a(tv t) — следовало бы назвать функцией «убытия», «вырождения» и т.п. Мы все же следуем общей традиции, считая рост относительным понятием, в положительном смысле означающим собственно увеличение, а в отрицательном — уменьшение.

Введенные характеристики процесса изменения фондовой величины легко выразить через функцию роста:

и

r(tltt2) fl(r„f2)-l

В свою очередь, легко получить выражения для функции роста через указанные величины

a(t{,t2) = 1 +r(trt2)

и

a(trt2)= 1 +j(trt1){t2-ll).

Функция роста a(tr ї2) показывает динамику изменения единицы фонда на периоде [/,, /,]. Так, если речь идет о вкладе в долларах, то функция a(t і t2) показывает, во сколько раз увеличится каждый доллар вклада на промежутке времени [/р t2].

Для стандартной модели процентного роста с постоянной (эффективной) годовой ставкой / имеем при tv t2 > tQ

S(tl) = S{i,){l+if". Тогда функция роста имеет вид

«(л.'Х'+'Г1

и, следовательно, она стационарна, т.е. зависит только от длины t — t} соответствующего промежутка [/ / ].

Если f2 — /, = 1, получаем единичный (нормированный) коэффициент роста

a = ax = a{tvtx +1)введенный в гл. 8.

В этом случае момент открытия вклада несуществен, важен лишь его срок. Заметим, что для простых процентов это уже не так, поскольку для

j(0=5(/,)(i+i-(/-/„)), i>t0

имеет место равенство

т.е. функция роста существенно зависит от момента tQ открытия вклада, о чем уже говорилось.

Выше была определена функция роста я(/р Л,) для пар /, > /0, удовлетворяющих условию fj < tv поскольку именно в этом случае функция a(lv t2) характеризует степень изменения фондовой величины S(t) на промежутке [г,, г2]. Функция a{1v t2) играет для фондовой величины S(t) (финансового процесса) ту же роль, что коэффициент капитализации a(f, г) для финансового закона капитализации (см. § 1.4). Однако определение (9.12) можно рассматривать и для пар /р t2 с обратным порядком, т.е. для / < tr Тогда уместнее говорить о функции дисконтирования, а не роста и писать не a(tv /2), a v{tp t2), т.е.

Таким образом, v(tvt2) играет для фондовой величины S(t) туже роль, что коэффициент дисконтирования для закона дисконтирования (см. 1.4).

Поскольку функции a{tv /) и v(tv f2) задаются одинаково и отличаются лишь областью определения, причем

то уместно ввести (подобно тому, как это сделано в § 1.4) одну общую всюду определенную функцию изменения (роста/дисконтирования). Для этой функции будем использовать оба обозначения а (г,, г) и v (гр /2) как взаимозаменяемые. Конкретный выбор зависит от контекста.

Свойствами функций роста и дисконтирования являются: — нормированность:

a(t, t) = v(t, 0=1;

транзитивность: для любых t2>t2>t{> tQ

a{tvt2) a{tvt5)=a{tvt)

v(tv t) = v{tv t2)v(t2t /,);

самосопряженность: для любых tx, t2 > t0

v(tvt2)v{tvtx)=

или, что то же самое,

a{tvt2)a{tv /,)= 1. Первое свойство равносильно равенству

a{t,t)-M = X.

Второе следует из определения. Например, для первого равенства

имеем о/ „/

И наконец, самосопряженность тривиально — из свойств нормированное™ и транзитивности. В частности, для второго равенства получаем

a{tvt2)a{tvtx) = a{tvtl)=.

Итак, финансовый процесс, описываемый своей функцией состояния S(t), t > tQ (S(t) Ф 0), порождает две величины: одномерные коэффициенты роста и дисконтирования

, , S(t) , , S(t0) и общие (двумерные) функции роста и дисконтирования

Они связаны равенствами

a(t) = a(tQ, t); v(t) = v(t, tQ).

Кроме того, функции роста и дисконтирования удовлетворяют условиям нормированности, транзитивности и самосопряженности.

Наконец, функция состояния процесса S(t) однозначно восстанавливается по функции роста и любому состоянию S(t.) процесса в некоторый момент времени /:

S(t) = S{tl)a{tl,t). (9-И)

В частности,

S(t) = S(Qa(t0, t) = S(t0)a(t). (9.14)

Мы определили функцию роста по заданной функции состояния S(f) процесса (его траектории), Равенства (9.13) и (9.14) показывают, что процесс можно задавать функцией или коэффициентом роста. Задание процесса его коэффициентом или функцией роста означает задание (см. § 1.4) некоторого финансового закона капитализации (или дисконтирования). Различие состоит, во-первых, в выделении некоторого начального момента /0, во-вторых, свойства нормированное™ и транзитивности выполняются автоматически. Для финансового закона нормированность также выполняется, а транзитивность не всегда (см. § 1.4).

Тривиальный способ построения функции роста состоит в выборе произвольной ненулевой функции a(t), t> /0, которая будет играть роль коэффициента роста, и определения

Пример 9.2. Пусть

a(t) = l + t+t г>0.

Найти функцию роста a(t}, /2) и интенсивность роста d(t).

Решение. Поскольку £7(0) = 1, то a{t) — непрерывный возрастающий коэффициент роста. Соответствующая ему функция роста

Интенсивность роста процесса

S{r) = S0a(t), задаваемого этой функцией в точке г, имеет вид

w L WJ S(t) l + t+t1

Менее тривиальный способ состоит в использовании функции интенсивности роста. Такой подход позволяет заменить функцию двух переменных a{tv t2) функцией одной переменной <5(0• Однако он применим лишь для дифференцируемых функций роста.

Пусть S(t), t>tQ — положительный (S(t) > 0) процесс с функцией рос-таа(/], /2). Тогда интенсивность роста процесса Sb точке /определяется как

S(t + h)-S(t)

h^Q' " ' h->0 hS(t)

Считая функцию S(t) непрерывно дифференцируемой, получаем, что

5(') = |lnS(0,

откуда, в свою очередь

\%) = S((,)exp {'j8(t)dt

(9.15)

ил и, что то же самое,

a(il,t2) = Qxp J5(t)6t

U

Для функции дисконтирования имеем соответственно выражение

( h v(^,r,) = exp ~S(t)dt

V 'і

Таким образом, любая непрерывная функция <5(/), / > /0, порождает функцию роста a{tx, /2) некоторого финансового процесса. Эволюция процесса с начальным состоянием S(tQ) будет описываться выражением

J

Выполнение для функций a{tv Г2), определяемых равенством (9.15), свойств нормированности и транзитивности проверяется тривиальным образом. Так,

tf(f,f) = exp J5(r)dr

= еи=а

что подтверждает нормированность. С другой стороны, равенства

a(tvt2)a(t2^) = exp

js(r)dr exp jS(r)d

)

)

= exp

j<5(r)dT+j<$(T)dr

= exp j5(r)dT =a(titt3)

подтверждают свойство транзитивности.

В схеме сложных процентов рост описывается функцией

где

es = 1 + /;

/— эффективная нормированная ставка.

Интенсивность роста в этом случае постоянна, т.е. <5(/) = 8 — const во

■ всей области определения процесса. При этом функции роста и дисконтирования имеют вид , .

и

v(t)-Q Х >.

В частности, для непрерывной модели накопительного счета

и в случае f = О Аналогично

*(/,) = ^,(5(/)) = 5(0е^м->

и для Т{) = О

s0 = pv0(s(t)) = s(t)v(t)=s(t)c*.

Пример 9.3. Пусть интенсивность роста (в годовой шкале) 0,09. Найти:

а) накопленную стоимость за два года суммы .^500;

б) текущую (приведенную) стоимость суммы М2000, отнесенной к кониу 5-го года.

Решение.

а) 5, = 500еида2 = 604,62(Л>;

б) Su 2000e-,W9-5 = Ш5,26( :#).

Мы вывели соотношение (9.15) в случае непрерывной интенсивности роста S(t), что равносильно непрерывной дифференцируемое™ S(t) и a{tv Г,). Однако это равенство остается справедливым и в более общих случаях, в частности для кусочно-гладких функций S{t).

Пусть

л

[*о> + °°) = и[т*-и^)

и функция 8(f) кусочно-непрерывна относительно этого разбиения. Иными словами, 8(f) непрерывна на интервале (тк , тк) и существуют односторонние конечные пределы в концах этих промежутков. Тогда формула

Л,

с(/„г2) = ехр J8(t)6t

определяет кусочно-гладкую нормированную и транзитивную функцию роста. Так, если S(t) — кусочно-постоянная функция:

то для получим

ё1 при/0=т0</<т,; >2 приг,</<т2; )3 приг2<ґ<т3;

<S„ '.При !„_!</<°о,

где h = г т ..

Как следствие этой формулы, в частности, получаем

j(/)=,s(On^c

(9.16)

ї=і

Если іА — эффективная нормированная ставка на промежутке

и формула (9.16) переходит в формулу (8.17). Пример 9.4. Пусть

0,01 при0</<1; 0,05 при1<г<5; 0,08 при5</<10; 0,2 при/>10.

Найти коэффициент роста, соответствующий этой интенсивности. Решение. Так как /0 = 0, то

a{t) = в(0, /).

Для 0 < / < 1 имеем

д(г) = ехр ]о,ОЫт

0.0ІГ

= е

Для 1 </< 5

a(t) = ехр

Jo,01dr + Jo,05dT

0.01 0.05(Ы) 0,01+0.05(^-1)

=е е =е .

Для 5<г< 10

a(t) = ехр

J0,01dT + |0,05dT+|0,08dT

= ехр[0,01 +0,05-4 + 0,08(ґ-5)] = ^2]+°m^.

Наконец, если t > 10, то

а (/) = ехр

1 5 [О і

Jo,01dr + J0,05dT + j0,08dr + J0,2dr

откуда

и,следовательно,

і/я»

В общем случае за любой период Л коэффициент роста

a(h) = а(0, h) = e5h.

С другой стороны,

о, = 1 + L

поэтому

V)='

е^-1 А

Аналогично выражается единичный коэффициент дисконтирования

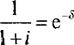
Коэффициент дисконтирования за произвольный период к

_ е-5А

п

Эти равенства определяют, в свою очередь, нормированную учетную ставку

d = 1-е"5

и учетную ставку за период h

d=-v=e~Sh.

h ( h

Пример 9.5, Интенсивность роста в годовой шкале равна 0,1 для всех г. Найти номинальные и фактические (за период) процентные и учетные ставки по вкладам: а) на 7 дней; б) 1 мес; в) 6 мес.

Решение. Поскольку

/Л=с**-1; 4=1-е-Л; iw=Uh; dh]=dh/h,

то для: а)

/А-=е^ -1 = 0,00192; dh=-t* =0,001916; /(Л) = 0,1001; d[h) = 0,0999;

б) =

/д =е^ -1 =0,0084; dh = 1-е~^ =0,0083; /(,.= 0,1004; rf(4)= 0,0996;

в) h = \:

ih=t? -1=0,0513; dh=l-e~^ =0,0478; =0,1025; </(А} = 0,0975.

Таким образом, использование интенсивности роста (силы процентов) позволяет получить простые выражения как для самого процесса роста, так и для всех видов ставок и характеризующих его коэффициентов, а также легко переходить к общему случаю переменных ставок. В последнем случае достаточно просто считать интенсивность переменной. Благодаря этим обстоятельствам в финансовом анализе модели роста задаются с помощью интенсивности. В следующей главе будет рассмотрена одна из таких моделей.

Вопросы и упражнения

Дайте определения средней скорости и средней и мгновенной интенсивноетей финансового процесса S{i).

Как связана интенсивность процентного роста с различными типами ставок, описывающих процесс накопления?

Докажите, что коэффициент роста и интенсивность для предельного процесса

1іт5^т'(г), где ^'"'(О — процесс роста по/л-кратно начисляемой номинальной ставке

/(я) =гу} совпадают с пределами коэффициента роста и интенсивности процесса S{"'- ) при т —> 00.

Какой вид имеет интенсивность роста по схеме простых процентов?

Докажите, что процесс роста с постоянной интенсивностью совпадает с процес-сом роста в схеме сложных процентов.

Задачи

1. Пусть S(t) = г V. Найдите среднюю скорость и среднюю интенсивность на отрезке [О, 11. Найдите мгновенную интенсивность в момент/= I.

. 2. Докажите, что для непрерывного дважды дифференцируемого процесса S(t) справедливо уравнение ,

где a(t) — одномерный коэффициент роста.

Величина S(t) фонда представляет собой квадратичную функцию. За первые полгода фонд увеличился на 20\%, а за год — на 80\%. Найдите интенсивность роста в конце года.

Пусть два фонда имеют одинаковые начальные состояния. Накопление в нервом фонде осуществляется по схеме простых процентов, а во втором — по схеме сложных процентов по той же ставке. Найти момент времени, в который разность между состояниями (накоплениями) первого и второго фондов будет максимальной.

Рост активов фонда А осуществляется по постоянной простой учетной ставке 5\%, а рост активов фонда Б — по простой процентной ставке 10\%. В какой момент времени интенсивности роста этих фондов совпадут?

Фонд растет с интенсивностью S(t) ~ 0,05г, 0 < г < 1, Найдиге эквивалентную ставку роста за период [0, 1 ].

Начальная величина фонда .#100 000. Найдите величину фонда*н конце 20-ю года, если интенсивность роста 6(г) = 0,05/(1 + t)2.

24-5169