14.7. вычисление внутренней доходности

14.7. вычисление внутренней доходности

В предыдущих параграфах отмечены некоторые трудности, связанные с вычислениями внутренней доходности. Основная состоит в неоднозначности самого определения внутренней доходности для произвольных потоков платежей, порождаемых данной финансовой сделкой. Но даже в тех случаях, когда денежный поток СРсделки обеспечивает единственность решения балансового уравнения

PVp(CF,y) = Q, у>-, (14.38)

(например, в случае нормального потока), нахождение числового значения, т.е. решение этого уравнения, может быть трудоемким делом.

В общем случае уравнение (14.38) (в исходной временнбй шкале) является трансцендентным. Выбор общей меры для критических промежутков, описанный в предыдущем параграфе, приводит к алгебраическому уравнению, в котором левая часть представляет собой многочлен, причем, как правило, большой степени и тем большей, чем больше платежей в потоке CFw меньше общая мера. С вычислительной точки зрения основная проблема состоит в том, что уравнение (14,38) определяет внутреннюю доходность лишь неявно в отличие, например, от базовой формулы (14.2), с помощью которой доходность за период вычисляется непосредственно.

Несмотря на перечисленные трудности, все же вычисление внутренней доходности исходя из балансового уравнения (14.38) не представляет особых проблем, поскольку имеются методы (алгоритмы) вычисления корней таких уравнений с любой степенью точности. Все эти методы являются итеративными процедурами, порождающими последовательность приближенных значении

где у0 — некоторое начальное, задаваемое как параметр процедуры, значение, а все последующие значения ук, к = 1,2, — функции от предыдущих значений:

Л=Ф(Л-1»Л-2.-»л)-Чаще всего используется простая итерационная схема

Л=Ф(Л-і)>

в которой очередное значение корняук получается применением одной и той же последовательности операций к непосредственно предшествующему значениюуА г

Корректные алгоритмы вырабатывают последовательность приближенных значений, сходящихся к искомому точному решению

їту„=у.

Конечно, точное решение представляет собой лишь предельное значение, и на практике итерационные вычисления прерываются при достижении требуемой точности є > 0:

Если уравнение (14.38) имеет несколько корней, то точное значение, являющееся пределом порождающейся алгоритмом последовательности приближенных значений, зависит от начального приближения у0. Для различных начальных приближений один и тот же алгоритм может порождать последовательности, сходящиеся кразным пределам. Более того, при некоторых начальных значениях порождаемая последовательность может вообще не сходиться. Обычно в описании алгоритмов содержатся рекомендации по выбору начальных приближений, обеспечивающих сходимость последовательности приближений в заданной области.

Мы не будем приводить здесь алгоритмы решения уравнения (14.38), поскольку большинство из них хорошо известны и содержатся в большинстве руководств по численным методам (см. [2]). Вместо этого опишем приближенные методы, основанные на замене (преобразовании) самого уравнения баланса. В них вместо сложного уравнения (14.38) решают другое существенно более простое. Упрощение делается с таким расчетом, чтобы, во-первых, оно позволяло получить явное решение уравнения, обычно в виде рационального выражения от исходных данных (элементов потока), и, во-вторых, чтобы это решение было бы удовлетворительным приближением к точному решению исходного уравнения (14.38). В частности, такой подход позволяет получать хорошие начальные приближения для итерационных методов, поскольку чем выше точность начального приближения, тем меньшее число итераций необходимо для получения приближенного решения с заданной точностью.

Методы вычисления внутренней доходности, основанные на преобразовании уравнения баланса (14.38), обычно используются в тех случаях, когда точное описание потока платежей CFневозможно или затруднительно. Поэтому вместо потока CF оперируют его обобщенными характеристиками. Особенно часто такой подход используется при оценке работы крупных финансовых институтов, таких, как инвестиционные или пенсионные фонды, банки, страховые компании и т.п. Выше деятельность таких институтов была описана нами в рамках модели фонда, представляющего собой счет с переменным капиталом, состояния которого задаются функцией S(t) и внешним потоком CF (дискретным, непрерывным или общим). Ниже приведен один из методов, позволяющий получить приближенную оценку внутренней доходности операций фонда на некотором периоде.

Рассмотрим работу фонда за период [/0, rj, причем без потери общности можно считать, что этот период имеет единичную длину T-r,-t,= l.

Пусть г0 = т0 < Tj <... < тп = /, — критические моменты операций фонда за период [г0, ff]. Положим, как и выше,

^■=^К"). v:=v{*i), к=о,,...,п.

— стоимости активов фонда непосредственно перед и сразу же после критического момента тк. При этом ^=К0~=К0+ — начальная, 'd VnV~ — конечная стоимости активов фонда. Разность

— ^-і> = 1,2,л, можно рассматривать какполный инвестиционный доход, полученный фондом за критический период [rk_ р tJ. При этом платежи потока в критические моменты тк имеют вид

С =-У

Ск=К~К* к = ,2,...9п-.

Отсюда

/ у _ у+ у~ V •

Л=КГ-(П-1 -^-,)-^-, =(^-П"-,)+с*-1. *=2,з,...,«.

Суммируя все равенства, получим или

VH-Va=I-N, (14.39) где / — суммарный полный доход фонда; N = NV(CF) — нетто-величина внешнего потока.

Пусть теперь у — внутренняя доходность фонда. Тогда согласно ее определению можно записать

К = К(1 + у)-ЪСЛ^уГ'(14.40) Используя равенство (14.39), уравнение (14.40) перепишем в виде

/ = *>-ІФ + уГ'-і]. (14.41)

Заметим, что выражение [(l + yf 4 -1 представляет собой доходность за период [тк, г,].

Используя приближенное равенство

і+УГ"-і]-('.-ь)у,

означающее замену эффективной доходности (у слева) нормированной простой доходностью {у справа), уравнение (14.41) можно переписать в виде

^-EQ(/,-tt)

(14.42)

к=1

= *o-Zc*(A-t*)(14.43)

Выражение в квадратных скобках называют средневзвешенным (по времени) капиталом

п-ї

V =

ср

1 Vt-Zck(t,-Tk)

Ь=1

Wo

Подчеркнем еще раз, что здесь рассмотрен случай, когда период оценки фонда является единичным, т.е. /, — tQ = 1, что обеспечивает соответствующую размерность величины V .

Напомним, что согласно принятому соглашению дополнительные инвестиции рассматриваются как расходы и, следовательно, в потоке CFзадаются отрицательными значениями, поэтому величины Ск будут отрицательными.

Из (14.42) и (14.43) окончательно получаем, что приближенная оценка для внутренней доходности за (единичный) период задается формулой

У*ї/К>(14.44) В качестве примера рассмотрим случай равномерного поступления инвестируемого капитала, т.е. считаем CF постоянной рентой (заметим, что с точки зрения фонда платежи ренты — это расход). Тогда

С = С —

С =С<0

я1

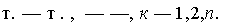к=

П к=х П~л 1

Заметим, что выражение С{п — 1) есть не что иное, как нетто-величи-на потока CF, представляющего постоянную ренту, т.е. С{п 1) = N

Таким образом, согласно формуле (14.43) средневзвешенный капитал для постоянной ренты будет определяться формулой

КР = К-х. (14.45)

Отсюда, используя (14.39),

1 у +v _ /

Подставляя это выражение для V в формулу (14.44), получаем прибли-женную формулу для оценки внутренней доходности фонда при равномерном поступлении инвестированного капитала:

2/

У

Эта формула была впервые выведена известным математиком Г. Харди в 1890 г. [32] для общего внешнего потока CF.

Приведенное доказательство легко обобщается на случай произвольного потока CF — суммы дискретной части CFiA) с платежной функцией C(t) и непрерывной части СЯН) с плотностью /Дґ). В этом случае балансовое уравнение (14.38) остается тем же самым, но нетто-величина потока находится по формуле

N = C(/) + j/j(/)tf,

а уравнение для внутренней ставки (доходности) принимает вид К = Ч^У)~ і С(/)(і + уГ'-)аі(/){НуГ'<і/

(по-прежнему считаем, что tx t0 = 1, т.е. рассматриваем единичный интервал оценки фонда).

Действуя таким же образом, что и в дискретном случае, можно получить приближенное равенство

Ыу

К Хс,.(ч-0-Й0('.-')<»>

'o<r<h

где выражение в квадратных скобках представляет собой (по определению) средневзвешенный капитал. Например, для чисто непрерывного потока (С(г)=0) с постоянной плотностью fi(t) = —ц0 получаем, с одной стороны, а с другой —

откуда получаем

г ср го 2 '

т.е. упоминавшееся выше выражение для средневзвешенного капитала при равномерном его поступлении.

Л р и мер 14. ] 7. Пусть начальная стоимость активов пенсионного фонда на начало года ,#500 ООО, а инвестиционный доход фонда за год #40 ООО. Взносы за год составили .#25 ООО, а выплаты фонда составили #36 ООО. Найти конечную стоимость и доходность фонда за год, предполагая равномерное распределение взносов и выплат.

Решение. Согласно условию Va 500 000; / = 40 000 и

N = -25 000 + 36 000 = 9000( ;#). Тогда на основании (14.39) и (14.45) находим

V = К0 + /-ЛГ=531 000(.#),

Следовательно,

Vc р = Kn IN = 500 000 4500=495 500(у#).

2-40000 _Л|£1С

^~ 495500 ~ или годовых.

Пример 14.18. Пусть стоимость активов фонда на начало года #100 000. К 1 марта стоимость активов возросла до .#120 000 и 1 марта в фонд поступило дополнительно #30 000. К 1 ноября активы фонда составляли .#160 000 и 1 ноября фонд выплатил .#40 000. Найти взвешенную по времени и денежно-взвешенную (внутреннюю) доходности операций фонда, если к концу года активы составляли .#130 000.

Решение. Временно-взвешенная доходность

У 0,3887, или 38,87\% за год.

и] 1 1,5 1,2

Для определения внутренней доходности сначала найдем согласно (14.39) обший доход из уравнения баланса

130 000 100 000 + 30 000 40 000 + /.

Откуда

/ = 40 000( .#).

Средневзвешенную величину капитала вычисляем по формуле (14.43):

V = 100 000+-■ 30 000--• 40 000= 115 833,33( Ж). 4 6

39-5169

Следовательно, приближенное значение для внутренней доходности

40000 Л,.„ ^ S 115833 33 ' ' или 34,53\% за год.

В заключение приведем еще одну приближенную формулу для внутренней доходности, используемой в оценке эффективности кредитных операций. Речь идет о внутренней ставке для потребительской схемы погашения долга.

Напомним, что в потребительской схеме кредит на сумму Р, выданный на срок п лет по годовой потребительской ставке /с, погашается пт одинаковыми платежами

С= У , с (14.46) пт

где т — число выплат в году

Обычно внутреннюю ставку, эквивалентную потребительской, ищут в виде номинальной ставки/т), такой что соответствующая ей ставка / = і за период h= /т между выплатами,

т

является внутренней ставкой потока

CF = {(0,-P);(kyC), А: = 1,2 Лт},

Точное уравнение для ставки / приводит к алгебраическому уравнению степени пт.

Вычислим ставку / другим способом. Считая, что каждый платеж С включает процентную

СПр = Р— т

и основную

части, где N = пт — общее число платежей, составим баланс общей суммы процентов из условия (приближенного) равенства, с одной стороны, всех процентных выплат по потребительской ставке / а с другой, — общей суммы процентов на остатки долга после каждого периода по ставке /.

Начальный долг S0 — Р. Остаток долга после первой выплаты

N N

после второй

2Р N-2

N N

и т.д.

Соответственно проценты по ставке / за первый период

за второй

Il = SQi = Pi = -Ni P(N-).

N

/2=5,і =

и т.д.

Общая сумма процентов на остатки долга

fN N-l Р^

/ = /,+/2+...+/*=/

N /V N N +

= /-(1+2+... + *) = //» 2

(14.47)

С другой стороны, общая сумма процентных выплат в потребитель-

ской схеме составляет

I = Pin.

с

Приравнивая выражения (14.47) и (14.48), получим

N+]

Pin~iP

(14.48)

откуда

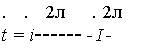
N+l с пт+ Соответствующая номинальная годовая ставка

(14.49)

Г '=mi=ic

л/л + 1

Пример 14.19. Пусть потребительский кредит на сумму .#12 тыс. сроком на год получен по потребительской ставке / =12\% годовых. Долг погашается одинаковыми ежемесячными платежами. Найти размер платежей и приближенное значение внутренней ставки по этому кредиту.

Решение. Общая сумма процентов за год согласно (14.48)

/= Pi( = 12000 0,12 = 1440(.#).

Тогда полная сумма

S = p+ /= 13400(;#). Теперь по формуле (14.46) можно найти величину ежемесячного платежа

12 v ■

Внутренняя месячная ставка согласно (14.49)

/,,=0,12^ = 0,018462,

или 1,85\%, что соответствует номинальной годовой ставке

/ш-12-/ж-0,2215,

или примерно 22\% годовых.

Вопросы и упражнения

Дайте определения: а) доходности сделки за период; б) простой доходности сделки; в) эффективной доходности сделки.

Что такое доходность актива и портфеля активов? Какие предположения подразумеваются при определении этих понятий?

Опишите основные виды усреднения доходностей за последовательные периоды времени. Определите взвешенные по времени и денежно-взвешенные доходности.

Что такое внутренняя доходность сделки? Запишите уравнение для внутренней доходности сделки с заданным порождающим потоком платежей.

Приведите критерии единственности внутренней доходности сделки с заданным потоком платежей. *

Опишите приближенный метод Харди вычисления внутренней доходности.

Задачи

В начале года вы купили акции компании А по .#340 за акцию, а год спустя продали их по .#390 за штуку. Годовой дивиденд составил .#15 на акцию. Найти доходность акции корпорации А за год. Какова текущая доходность этой акции?

В начале года вы купили 100 акций компании А по .#600 за акцию, а спустя год продали их по .#610 за акцию. Годовой дивиденд составил .#30 на акцию. Каков ценовой доход от продажи акции? Каков текущий доход? Какова доходность акций за год?

Инвестор, обладая свободным капиталом в #500 000, инвестирует его в портфель активов, дающих 10\% годовых текущей и 20\% годовых ценовой доходностей. Планируемый инвестиционный период 3 года. Найти капитал инвестора в конце периода.

Финансовая фирма управляет средствами спонсоров пенсионных схем. Один из ее клиентов предоставил в управление фирмы $200 млн. За последние три месяца денежный поток, связанный с портфелем этого клиента, составил S20 млн — S8 млн и $4 млн.

На конец 3-месячного периода рыночная стоимость портфеля была равна S208 млн. а) Чему равна денежно-взвешенная доходность портфеля этого клиента за 3-месячный срок? б) Предположим, что выплаченные во втором месяце S8 млн представляют собой изъятие спонсором пенсионной схемы части размещенных средств. Какова была бы денежно-взвешенная доходность, если бы это изъятие не производилось?

Чему будет равна среднегодовая доходность портфеля, если: а) среднемесячная доходность портфеля 1,23\%? б) средняя за квартал доходность портфеля 1,78\%?

Пусть портфель состоит из четырех активов. Рыночная стоимость и реализованная доходность каждого актива за некоторый фиксированный период задаются табл. 14.1. Вычислите доходность этого портфеля за период.

7. Пусть два финансовых менеджера (в месяц) получили следующую доходность (табл. 14.2).

а) Найти среднюю арифметическую ежемесячную доходность для каждого из менеджеров, б) Найти средневзвешенную по времени ежемесячную доходность для каждого из менеджеров, в) Почему ятя первого менеджера среднеарифметическая доходность сильнее отличается от взвешенной по времени ежемесячной доходности, чем для второго?

8. Стоимость портфеля, млн S, в 1996 г. задается табл. 14.3.

В начале апреля (01.04.96) было дополнительно инвестировано S50 млн. В начале июля (01.07.96) было инвестировано еще S50 млн. Никаких изъятий капитала в І996 г. не было. Найти доходность, реализованную менеджером за 1996 г.