Глава 3. моделирование случайных событий и величин
Глава 3. моделирование случайных событий и величин
Имитационное моделирование это численный метод исследования систем и процессов с помощью моделирующего алгоритма.
Каждый раз, когда на ход моделируемого процесса оказывает влияние случайный фактор, его действие имитируется с помощью специально организованного розыгрыша (жребия). Таким образом строится одна случайная реализация моделируемого явления, представляющая собой как бы один результат опыта. По одному опыту, конечно, нельзя судить о закономерностях изучаемого процесса. Но при большом числе реализации средние характеристики, вырабатываемые моделью, приобретают свойство устойчивости, которое усиливается с увеличением числа реализации.
Бросание жребия можно осуществить вручную (выбором из таблицы случайных чисел), но удобнее это делать с помощью специальных программ, входящих в состав программного обеспечения ЭВМ. Такие программы называют датчиками, или генераторами, случайных чисел.
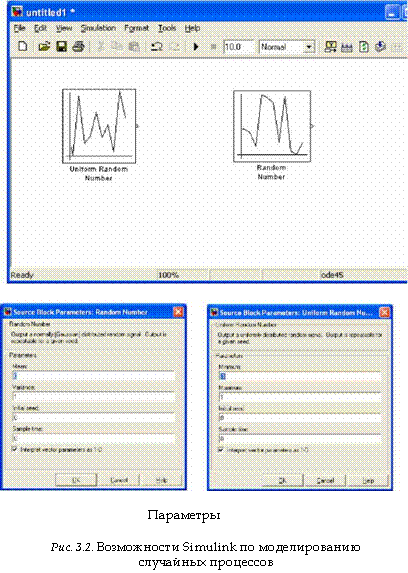
В программе Simulink/Matlab имеются стандартные процедуры или функции, которые генерируют случайные (точнее, псевдослучайные) величины с равномерным распределением.
В Simulink/Matlab имеются очень широкие возможности по моделированию различного рода случайностей (событий, процессов, функций и т.д.) (рис. 3.1 и 3.2).
38

39
 40
40
При моделировании экономических процессов возникает необходимость в моделировании различных случайных факторов. Эти факторы в зависимости от их природы могут быть отражены в модели как случайные события, случайные величины (дискретные или непрерывные) или как случайные функции (процессы).
Например, если с помощью создаваемой имитационной модели предполагается исследовать надежность вычислительной системы, то возникновение отказа будет представлено в модели как случайное событие. Если же модель предназначена для оценки временных параметров процесса обслуживания клиентов в автомастерской, то интервал времени до появления очередного клиента удобнее всего описать как случайную величину, распределенную по некоторому закону.
§1. Моделирование случайных событий 1.1. Моделирования простого события
Пусть имеется событие А, вероятность наступления которого равна Ра. Требуется выработать правило, при многократном использовании которого частота появления события стремилась бы к его вероятности. Выберем с помощью датчика случайных чисел, равномерно распределенных в интервале (0,1), некоторое число z и определим вероятность того, что
Pa
P(z < Pa) = J f(x)dx =Pa.
0
z < Ра. Для случайной величины z с равномерным распределением справедлива следующая зависимость:
Таким образом, вероятность попадания случайной величины в интервал (0,Ра) равна величине Ра. Поэтому если при розыгрыше число z попало в этот интервал, то следует считать, что событие А произошло. Противоположное событие (не А) произойдет с вероятностью (1 Ра) в том случае, если z > = Ра.
41
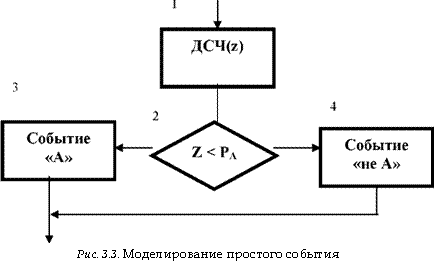 Процедура моделирования простого события в имитационной модели описывается алгоритмом, схема которого показана на рис. 3.3.
Процедура моделирования простого события в имитационной модели описывается алгоритмом, схема которого показана на рис. 3.3.
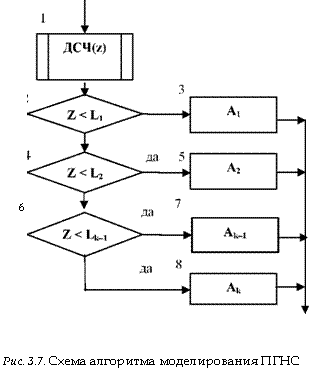
Оператор 1 обращается к датчику случайных чисел, генерирующему случайную величину z. Оператор 2 проверяет условие z < Ра. Если оно выполняется, считается, что произошло событие А. В противном случае считается, что произошло противоположное событие (не А).
На рис. 3.4 показан пример реализации модели случайного события с помощью Simulink.
Блок Uniform Random Number генерирует случайные числа (СЧ), равномерно распределенные на интервале [0;1]. Для этого выполнены следующие исходные установки его параметров:
Minimum (нижняя граница диапазона): 0;
Maximum (верхняя граница диапазона) : 1.
Третий параметр Sample time в данном случае позволяет задавать количество СЧ, которые будут сформированы
42
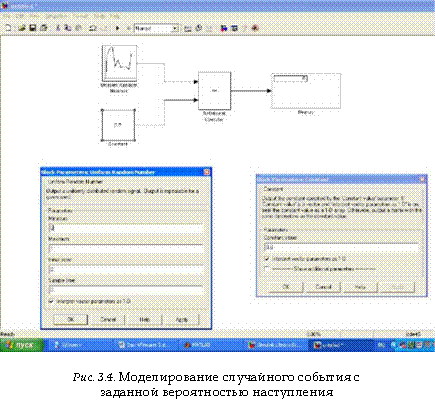 блоком в течение интервала моделирования: при Sample time, равном 0, новое случайное число генерируется через каждые 0,02 единицы модельного времени; при Sample time, равном интервалу моделирования, генерируется только одно СЧ. На рис. 3.4 приведен пример блок-диаграммы, позволяющей моделировать появление случайного события А при Ра = 0,4.
блоком в течение интервала моделирования: при Sample time, равном 0, новое случайное число генерируется через каждые 0,02 единицы модельного времени; при Sample time, равном интервалу моделирования, генерируется только одно СЧ. На рис. 3.4 приведен пример блок-диаграммы, позволяющей моделировать появление случайного события А при Ра = 0,4.
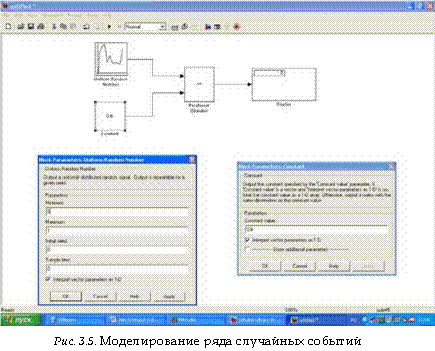
На рис. 3.5 показано моделирование нескольких случайных событий на интервале моделирования 6 единиц модельного времени.
43
 Особенностью блока Uniform Random Number является то, что он в каждом сеансе моделирования генерирует одну и ту же последовательность СЧ. Для изменения генерируемой последовательности необходимо вручную изменить значение его параметра Initial seed. При проведении большого числа повторных экспериментов с целью накопления статистических данных это не очень удобно. Поэтому для моделирования случайных событий можно воспользоваться генераторами СЧ, входящими в состав компоненты Matlab, которая называется Toolboxes-Statistics (средства статистического анализа). Данная компонента доступна для использования в том случае, если она включена в рабочую конфигурацию пакета Matlab. Toolboxes-Statistics, как и другие инструментальные приложения, представляет собой набор специализированных функ44
Особенностью блока Uniform Random Number является то, что он в каждом сеансе моделирования генерирует одну и ту же последовательность СЧ. Для изменения генерируемой последовательности необходимо вручную изменить значение его параметра Initial seed. При проведении большого числа повторных экспериментов с целью накопления статистических данных это не очень удобно. Поэтому для моделирования случайных событий можно воспользоваться генераторами СЧ, входящими в состав компоненты Matlab, которая называется Toolboxes-Statistics (средства статистического анализа). Данная компонента доступна для использования в том случае, если она включена в рабочую конфигурацию пакета Matlab. Toolboxes-Statistics, как и другие инструментальные приложения, представляет собой набор специализированных функ44
ций (см. рис. 3.1), реализованных в виде М-файлов. Ее особенностью является то, что для нее отсутствует набор блоков, который включался бы в библиотеку Simulink. Поэтому в процессе моделирования статистические функции следует использовать один из двух способов:
выполнять в командном окне Matlab;
• включать в вычисляемое выражение в тех блоках S-модели, в которых разрешено использование М-функций. Категория функций Random Namber Generation (генераторы случайных чисел) обеспечивает формирование значений случайной величины, распределенной по определенному закону с задаваемыми параметрами. Генератор непрерывной СВ, равномерно распределенной в заданном интервале, называется unifrnd. Обращение к данной функции имеет вид unifrnd (А, В, М, N), где А, В границы диапазона распределения, а параметры М, N задают размер генерируемой матрицы случайных чисел. Если параметры М, N опущены, то генерируется единственное значение случайной величины.
При моделировании случайного события функция unifrnd может быть указана в качестве параметра настройки следующих блоков:
Matlab Fcn (раздел Function&Tables );
Fcn (из того же раздела);
Constant (раздел Sources).
Напоминание из теории вероятностей
Случайная величина (СВ) величина, которая в результате опыта может принимать некоторое неизвестное заранее значение.
Дискретная случайная величина (ДСВ) принимает конечное (счетное) множество возможных значений.
Непрерывная случайная величина (НСВ) может принимать любые значения из некоторого интервала.
Случайная величина задается функцией распределения F(x) = P(X < x). Если F(x) непрерывна и дифференцируема, то непрерывная случайная величина задается плотностью вероятностей f(x), которая является производной от F(x).
45
F (x) = J f (x)dx
— 00
f(x)=F'(x).
Свойства функции распределения
При -да < x < + да, 0 = < F(x) = < 1;
Неубывающая, т.е при x2 < xi F(x2) > F(xi);
Имеет место F(+co) = 1 и F(-co) = 0;
Вероятность попадания СВ (х) в интервал (а,Ь).
Свойства плотности распределения вероятностей
Неотрицательна f(x) > = 0
P(a < х < b) = F(b) — F(a)
00
J f(x)dx = F(o) — F( —o) = 1
Вероятность попадания в интервал (a,b)
00
P(a < x < b) = J f (x)dx
— CO
Математическое ожидание непрерывной случайной величины
да
M (X) = J x • f (x)dx
—да
Дисперсия непрерывной случайной величины
да
D(X) = M[x — M(X)]2 = J[x — M(X)]2 • f (x)dx
—да
46
 |
6. Среднее квадратическое отклонение
а(Х) = +V D(X).
1.2. Моделирование полной группы несовместных событий
Пусть имеется полная группа несовместных событий (ПГНС) Аі, Аг..., Ак с вероятностями Рі , Рг.., Рк . При этом выполняется условие
i=1
 |
Если случайное число z, генерированное датчиком случайных чисел с равномерным распределением в интервале (0,1), попало, например, на участок Рк-і, то это должно означать, что произошло событие Ак-1.
Действительно, если обозначить
i=1
то окажется справедливым выражение
L1
P(Lk_2 < z < Lk-) = J1 • dx =PkLk-2
47
Следовательно, произойдет событие, которое имеет вероятность Рк-1.
Процедура моделирования полной группы несовместных событий описывается алгоритмом, схема которого показана на рис. 3.7.
 |
48
Обсуждение Имитационное моделирование экономических процессов
Комментарии, рецензии и отзывы
