Глава 10. стратегические игры
Глава 10. стратегические игры
Цели
В данной главе показаны возможности использования одного из классов игровых моделей — так называемых стратегических игр — для принятия решений преимущественно экономического характера в условиях неопределенности. Дается общее описание стратегической игры и ее место в классификации игр. Подробно рассматривается класс стратегических игр двух лиц с нулевой, а также с постоянной ненулевой суммой. Определяется понятие равновесия в ифе в чистых и смешанных стратегиях. Представлен общий подход к играм указанного типа — сведение к соответствующей задаче линейного программирования.
После того как вы выполните предлагаемые в этой главе задания, вы будете уметь строить для различных ситуаций принятия экономических решений (там, где это возможно и целесообразно) соответствующую игровую модель, определяя:
• игроков и их стратегии;
• матрицу выигрышей;
• наличие или отсутствие седловых точек в чистых стратегиях;
• доминируемые стратегии;
• эквивалентную модель линейного программирования;
• оптимальные стратегии;
• цену игры.
Модели
Методы, основанные на теории игр, используются для принятия решений в условиях неопределенности. Игра — это математическая модель конфликтной ситуации, которая предполагает наличие следующих компонентов:
а) заинтересованных сторон;
б) возможных действий каждой из сторон;
в) интересов сторон.
В игре заинтересованные стороны называются игроками, каждый из которых может предпринимать не менее двух действий (если ифок имеет в своем распоряжении только одно действие, то он фактически не участвует в игре, поскольку заранее известно, что он предпримет).
Слово «игра» обозначает некоторый набор правил и соглашений, составляющих данный вид игры, например: футбол, шахматы и др.
В экономике модель поведения лиц в виде игры возникает, например, при попытке нескольких фирм завоевать наиболее выгодное место на конкурентном рынке или при желании нескольких лиц (компаний) разделить некоторое количество продукта (ресурса, финансовых средств) между собой так, чтобы каждому досталось как можно больше. Игроками в конфликтных экономических ситуациях, моделируемых в виде игры, являются производственные и непроизводственные фирмы, банки, отдельные предприниматели и другие экономические агенты. В военной области модель игры используется, например, для наилучшего выбора средств (из имеющихся или потенциально возможных) поражения военных целей противника или защиты от его нападения.
Для игр характерна неопределенность результата (исхода). Причины неопределенности относятся к трем группам:
1) комбинаторные источники (шахматы);
2) влияние случайных факторов (игра в орлянку, кости, карточные игры, где случаен расклад);
3) стратегическое происхождение: игрок не знает, какого образа действий придерживается его противник. Здесь неопределенность исходит от другого лица.
Игры, в которых неопределенность имеет стратегическое происхождение, называются стратегическими.
Таким образом, в стратегической игре действия предпринимают две стороны или более, в отличие от нестратегической игры, в которой действия предпринимает одна сторона, а остальные являются заинтересованными сторонами.
Стратегические игры классифицируют по следующим признакам:
1) число игроков (игра двух лиц, игра п (п > 2) лиц);
2) количество стратегий (конечные, бесконечные);
3) количество информации, имеющейся у игроков относительно прошлых ходов (игры с полной, игры с неполной информацией). Шахматы — пример игры с полной информацией;
4) принцип деления выигрыша (коалиционные, бескоалиционные).
Далее рассматривается модель конечной стратегической игры с полной информацией, в которой участвуют две стороны, имеющие противоположные интересы. Такую игру принято называть конечной игрой двух лиц с нулевой суммой.
1. Матричная игра двух лиц с нулевой суммой
В игре двух лиц с нулевой суммой (такую игру называют также антагонистической) принимают участие два игрока: игрок 1 и игрок 2. В распоряжении каждого из них имеется множество стратегий. Под стратегией понимают совокупность правил (принципов), определяющих выбор варианта действий при каждом ходе игрока в зависимости от сложившейся ситуации. Пусть А = {а1, а2,...} — множество стратегий игрока 1, В = {b1, b2,...} — множество стратегий игрока 2. Элементы множества А — возможные стратегии (действия) игрока 1, элементы множества В — стратегии игрока 2. Условия игры представлены так называемой функцией выигрыша игрока 1: H(ai, bj), где аiÎА — i-я стратегия игрока 1, bjÎВ — j-я стратегия игрока 2. В игре с нулевой суммой выигрыш игрока 2 равносилен проигрышу игрока 1 и равен поэтому — H(ai, bj). Предполагается, что функция выигрыша обоим игрокам известна. Поскольку игроков всего двое и игра антагонистическая, коалиции невозможны.
Игра, в которой множества А и В стратегий игроков конечны, т.е. |А| < ¥, |В| < ¥, называется матричной. В этом случае функция выигрышей игрока 1 имеет вид матрицы, называемой матрицей игры (матрицей выигрышей, платежной матрицей) Н = {аij}m,n, i = 1,..., т; j = 1,..., п. Строки этой матрицы соответствуют стратегиям a1, а2, ..., аm игрока 1, столбцы — стратегиям b1, b2, ..., bn игрока 2. Элемент матрицы aij = H (ai, bj) — выигрыш игрока 1 в случае, когда он применит стратегию аi, а его противник — стратегию bj, i = 1, ..., т; j = 1, ..., п.
Элементы матрицы могут быть положительными, отрицательными или равными нулю. Случай, когда данный элемент матрицы положителен, означает, что игрок 2 в определенной ситуации должен уплатить игроку 1 сумму, равную значению этого элемента. Если данный элемент отрицателен, игрок 1 уплачивает игроку 2 сумму, равную абсолютному значению этого элемента. И наконец, если этот элемент равен нулю, никакой выплаты не производится. Таким образом, в игре двух лиц с нулевой суммой один игрок выигрывает столько же, сколько проигрывает другой (все выплаты производятся из «карманов» противников). Это и объясняет название — игра с нулевой суммой.
Игрок 1 стремится к максимальному выигрышу, игрок 2 — к минимальному проигрышу. Решить игру — значит найти оптимальные стратегии игроков и их выигрыши.
В игре двух лиц с нулевой суммой, как и в любой другой стратегической игре, исход зависит от поведения обоих игроков, которое основывается на так называемых правилах игры. Допустим, что по правилам игры игрок 1 может выбрать произвольную строку матрицы и, следовательно, может выбрать одно из чисел 1, 2, ..., т. Аналогично игрок 2 имеет возможность выбора произвольного столбца матрицы выигрышей и, следовательно, одного из чисел 1, 2,..., п. Исход (результат) игры и, следовательно, сумму, которую игрок 2 должен уплатить игроку 1, определяет элемент матрицы выигрышей, находящийся на пересечении строки, выбранной игроком 1, и столбца, выбранного игроком 2. Ни один из партнеров не знает, какую стратегию применит его противник. Таким образом, имеет место ситуация полной неопределенности, при которой теория вероятностей не может помочь игрокам в выборе решения.
Рассмотрим процесс принятия решений обеими сторонами более детально, предполагая, что игроки действуют рационально.
Если игрок 1 не знает, как поступит его противник, то, действуя наиболее целесообразно, не желая рисковать и считая, что противник также будет действовать целесообразно, он выберет такую стратегию, которая гарантирует ему наибольший из наименьших выигрышей при любой стратегии противника. Принято говорить, что при таком образе действий игрок 1 руководствуется принципом максиминного выигрыша. Этот выигрыш определяется формулой = 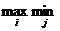 aij. Величина называется нижней ценой игры, максиминным выигрышем, или сокращенно — максимином.
aij. Величина называется нижней ценой игры, максиминным выигрышем, или сокращенно — максимином.
В свою очередь игрок 2, действуя рационально, выберет такую стратегию, которая гарантирует ему наименьший из возможных проигрышей при любых действиях противника. Принято говорить, что игрок 2 руководствуется принципом минимаксного проигрыша. Этот проигрыш определяется выражением = 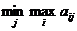 . Величина называется верхней ценой игры или минимаксом.
. Величина называется верхней ценой игры или минимаксом.
Принцип осторожности, который определяет выбор партнерами стратегий, соответствующих максиминному выигрышу или минимаксному проигрышу, часто называют принципом минимакса, а стратегии, вытекающие из этого принципа, — минимаксными стратегиями. Доказано, что всегда а 5 р, чем и объясняются названия «нижняя цена» и «верхняя цена». В случае когда нижняя цена игры равняется ее верхней цене, их общее значение называется ценой игры. При этом результат стратегической игры двух лиц с нулевой суммой можно определить, не приступая к фактической игре: вполне реален сценарий, когда партнеры, взглянув на матрицу, рассчитываются, пожимают друг другу руки и расходятся. Очевидно, что исход такой игры не изменится, если она будет повторена многократно, поскольку ни одному из игроков невыгодно отклоняться от своих минимаксных стратегий. Ситуация, в которой нижняя и верхняя цены игры совпадают, называется седловой точкой. Формальное определение: ситуация (ai*, bj*) ÎA ´ В называется седловой точкой, если
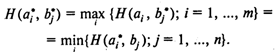
В седловой точке элемент матрицы аij* = H(ai*, bj*) является одновременно наименьшим в строке и наибольшим в столбце и, следовательно, соответствует цене игры. Однако существуют матрицы игры двух лиц с нулевой суммой (и таких игр большинство), для которых ¹ , т.е. седловая точка отсутствует. Исход такой игры определить труднее, поскольку какой-либо одной так называемой чистой оптимальной стратегии ни для одного игрока не существует. В таких случаях говорят, что решение игры в чистых стратегиях отсутствует, и рассматривают так называемое смешанное расширение игры, решение которой ищут в смешанных стратегиях. Смешанная стратегия игрока — это случайная величина, значениями которой являются его чистые стратегии. Для того чтобы задать смешанную стратегию игрока, необходимо указать вероятности (частоты), с которыми выбираются его первоначальные (чистые) стратегии. При этом предполагается, что игра повторяется многократно.

Здесь р1, р2,..., рm — вероятности использования игроком 1 в смешанной стратегии своих чистых стратегий a1, a2, ..., am; q1, q2, ..., qn — вероятности использования игроком 2 в смешанной стратегии своих чистых стратегий b1, b2, ..., bn.
Математическое ожидание выигрыша игрока 1:
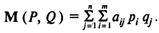
Смешанная стратегия, которая гарантирует данному игроку наибольший возможный средний выигрыш (или наименьший возможный средний проигрыш), называется его оптимальной смешанной стратегией, а стратегии, из которых складывается оптимальная смешанная стратегия, определяются как выгодные стратегии.
Пусть Р* — смешанная стратегия игрока 1,Q* — смешанная стратегия игрока 2. Ситуацию (P*,Q*), при которой М(Р, Q*) £ М(Р*, Q*) £ М(Р*, Q), называют седловой точкой смешанного расширения игры, а математическое ожидание выигрыша v = М(Р*, Q *) — ценой игры, причем всегда £ v £ .
Доминирование стратегий. Если платежная матрица такова, что каждый элемент некоторой строки i не меньше соответствующего элемента строки k и по меньшей мере один ее элемент строго больше соответствующего элемента строки k, то говорят, что стратегия а, игрока 1 доминирует его стратегию аi. Доминируемая стратегия не может быть оптимальной чистой стратегией игрока 1 и даже не может войти в его оптимальную смешанную стратегию с ненулевой вероятностью, поэтому ее можно исключить из рассмотрения, вычеркнув из матрицы строку k. Аналогично: если каждый элемент некоторого столбца j не больше соответствующего элемента столбца r и по меньшей мере один его элемент строго меньше соответствующего элемента столбца r, то говорят, что стратегия bj игрока 2 доминирует его стратегию br. Поэтому столбец r матрицы можно вычеркнуть.
Сведение игры двух лиц с нулевой суммой к задаче линейного программирования. Если седловая точка отсутствует, то общим методом решения игры любой (конечной) размерности является сведение игры двух лиц с нулевой суммой к задаче линейного профаммирования. Из основного положения теории стратегических игр следует, что при использовании смешанных стратегий существует по меньшей мере одно оптимальное решение с ценой игры v, причем £ v £ , т.е. цена игры находится между нижним и верхним значениями игры. Величина v неизвестна, но можно предположить, что v > 0. Это условие выполняется, поскольку путем преобразования матрицы всегда можно сделать все ее элементы положительными. Таким образом, если в исходной платежной матрице имеется хотя бы один неположительный элемент, то первым шагом в процедуре сведения игры к задаче линейного программирования должно быть ее преобразование в матрицу, все элементы которой строго положительны. Для этого достаточно увеличить все элементы исходной матрицы на одно и то же число d > 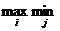 |aij|, где аij £ 0. При таком преобразовании матрицы оптимальные стратегии игроков не изменяются.
|aij|, где аij £ 0. При таком преобразовании матрицы оптимальные стратегии игроков не изменяются.
Допустим, что смешанная стратегия игрока 1 складывается из стратегий a1, a2,..., am с вероятностями соответственно p1, p2,..., pm (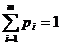 ,
, 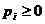 ). Оптимальная смешанная стратегия игрока 2 складывается из стратегий b1, b2,..., bn с вероятностями q1, q2,..., qn (
). Оптимальная смешанная стратегия игрока 2 складывается из стратегий b1, b2,..., bn с вероятностями q1, q2,..., qn (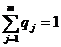 ,
, 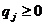 ). Условия игры определяются платежной матрицей
). Условия игры определяются платежной матрицей 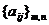 ,
, 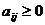 , i = 1,..., m; j = 1,..., n.
, i = 1,..., m; j = 1,..., n.
Если игрок 1 применяет оптимальную смешанную стратегию, а игрок 2 — чистую стратегию bj, то средний выигрыш игрока 1 (математическое ожидание выигрыша) составит р1a1j + р2a2j + ... + рmamj, j = 1,..., n.
Игрок 1 стремится к тому, чтобы при любой стратегии игрока 2 его выигрыш был не менее чем цена игры v и сама цена игры была максимальной. Такое поведение игрока 1 описывается следующей моделью линейного программирования:
v ® max (игрок 1 стремится максимизировать свой выигрыш),
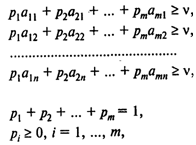
или, обозначив хi = рi/v, имеем
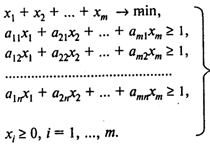
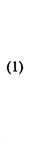
Причем
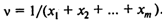
Поведению игрока 2 соответствует двойственная задача:

Задача (1) всегда имеет решение. Получив ее оптимальное решение 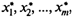 , можно найти цену игры
, можно найти цену игры 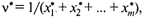 оптимальные значения
оптимальные значения 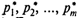 и, следовательно, оптимальную стратегию игрока 1. Если исходная матрица увеличивалась на d, то для получения цены первоначальной игры v* нужно уменьшить на d.
и, следовательно, оптимальную стратегию игрока 1. Если исходная матрица увеличивалась на d, то для получения цены первоначальной игры v* нужно уменьшить на d.
Справедливо и обратное положение: любую задачу линейного программирования можно свести к решению соответствующей игры двух лиц с нулевой суммой.
2. Матричная игра двух лиц с ненулевой постоянной суммой
Конечная игра, в которой сумма выигрышей обоих игроков не равна нулю и постоянна для всех сочетаний их чистых стратегий, называется матричной игрой двух лиц с ненулевой постоянной суммой. Пусть 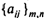 — матрица выигрышей игрока 1 и
— матрица выигрышей игрока 1 и 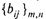 — матрица выигрышей игрока 2. Причем
— матрица выигрышей игрока 2. Причем 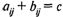 для всех
для всех 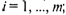
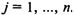 .
.
Такого рода игра сводится к игре двух лиц с нулевой суммой следующим образом:
1) каждому игроку выплачивается сумма с/2;
2) решается игра с нулевой суммой с матрицей выигрышей 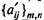 игрока 1, где
игрока 1, где 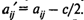
Действительно, в игре с преобразованной таким способом матрицей выигрышей игрок 2 получает сумму с/2 – аij для всех i = 1, ..., т; j = 1, ..., п, т.е. новая игра является игрой с нулевой суммой. При этом каждый игрок ничего не теряет от того, что каждый из них в игре получает на с/2 меньше, поскольку по с/2 они получили перед игрой.
Примеры
Пример 1. Выбор стратегии. Матрица некоторой игры имеет вид
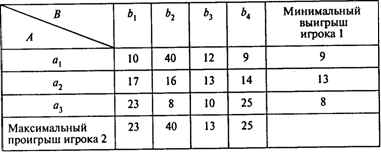
Найдите оптимальные стратегии игроков.
Решение. В этой игре игрок 1 имеет три возможные стратегии: а1, а2, а3 из, а игрок 2 — четыре возможные стратегии: b1, b2, b3, b4.
Рассмотрим процесс принятия игроками решения (предполагается, что они действуют рационально). Взглянув на таблицу, можно заметить, что если игрок 1 не знает, как поступит его противник, то, действуя наиболее целесообразно и считая, что противник будет действовать подобным же образом, он выберет стратегию а2, которая гарантирует ему наибольший из трех возможных наименьших выигрышей: 9, 13, 8. Другими словами, игрок 1 руководствуется принципом максиминного выигрыша. Этот выигрыш = 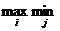 аij есть нижняя цена игры. Для нашего примера = 13.
аij есть нижняя цена игры. Для нашего примера = 13.
Игрок 2 рассуждает аналогично: если он выберет стратегию b1, ,то потеряет самое большее 23, если стратегию b2, то — 40, и т.д. В результате он выберет стратегию b3, которая гарантирует ему наименьший из четырех возможных проигрышей: 23, 40, 13, 25. Принято говорить, что игрок 2 руководствуется принципом минимаксного проигрыша. Этот проигрыш = 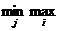 аij есть верхняя цена игры. Для нашей матрицы = 13.
аij есть верхняя цена игры. Для нашей матрицы = 13.
Ситуация (a2, b3) есть седловая точка, и = = 13 есть цена игры.
При наличии седловой точки ни одному из участников игры невыгодно отклоняться от своей минимаксной стратегии: он будет наказан противником тем, что получит меньший выигрыш.
Пример 2. Где строить?
Две конкурирующие крупные торговые фирмы Ф1 и Ф2 планируют построить в одном из четырех небольших городов Г1, Г2, Г3 и Г4, лежащих вдоль автомагистрали, по одному универсаму. Взаимное расположение городов, расстояние между ними и численность населения показаны на рис. 1.

Рис. 1
Прибыль каждой фирмы зависит от численности населения городов и степени удаленности универсамов от места жительства потенциальных покупателей. Специально проведенное исследование показало, что прибыль в универсамах будет распределяться между фирмами следующим образом:

Например, если универсам фирмы Ф1 расположен к городу Г1 ближе универсама фирмы Ф 2, то прибыль от покупок, сделанных жителями данного города, распределится следующим образом: 75\% получит Ф1, остальное — Ф 2.
Представьте описанную ситуацию как игру двух лиц.
В каких городах фирмам целесообразно построить свои универсамы?
Решение. Составим платежную матрицу игры, в которой игроком 1 будет фирма Ф 1, а игроком 2 — фирма Ф2. Стратегии обоих игроков: строить свой универсам в городе Г1, в городе Г2 и т.д. Элементы матрицы — прибыль фирмы Ф1 (в тыс. руб.), которая, как предполагается, пропорциональна (причем с одним и тем же коэффициентом) числу покупателей. Величина указанного коэффициента пропорциональности для выбора оптимального места размещения универсамов значения не имеет, поэтому примем его равным единице.
Платежная матрица имеет вид
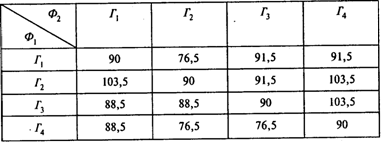
Рассмотрим примеры расчета значений элементов (Г1, Г2) и (Г3, Г4) матрицы.
Ситуация (Г1, Г2) означает, что фирма Ф1, строит универсам в городе Г1, а фирма Ф2 — в городе Г2. Число покупателей фирмы Ф1 складывается из покупателей четырех городов. Для ситуации (Г1, Г2) число покупателей из Г1: 0,75×30, из Г2: 0,45×50, из Г3 0,45×40, из Г4: 0,45×30, т.е. в сумме 76,5 тыс. руб. Для ситуации (Г3, Г4) число покупателей из Г1: 0,75×30, из Г2: 0,75×50, из Г3: 0,75×40, из Г4: 0,45×30, т.е. в сумме 103,5 тыс. руб. Элементы матрицы выигрышей фирмы Ф2 — дополнения до числа 150 (общее число жителей в четырех городах). Таким образом, имеет место игра двух лиц с ненулевой постоянной суммой, оптимальные стратегии которой те же, что и для соответствующей игры с нулевой суммой.
Полученная платежная матрица имеет седловую точку (Г2, Г2). Соответствующий элемент матрицы равен 90.
Таким образом, обеим фирмам следует строить свои универсамы в одном и том же городе Г2, при этом прибыль фирмы Ф1 составит 90 тыс., а фирмы Ф2 — 60 тыс. руб.
Пример 3. Двухпальцевая «игра морра».
Каждый игрок показывает один или два пальца и называет число пальцев, которое, по его мнению, показал его противник (ни один из игроков не видит, какое число пальцев на самом деле показывает его противник). Если один из игроков угадывает правильно, он выигрывает сумму, равную сумме числа пальцев, показанных им и его противником. В противном случае (если никто не угадывает) — ничья. Если оба угадали, то игроки платят друг другу одинаковую сумму, в результате также ничья.
Вопросы:
1. Существует ли в данной игре седловая точка в чистых стратегиях?
2. Кто из игроков в среднем выигрывает и сколько?
3. Как часто игрок 1 должен говорить, что его противник показал два пальца?
4. Как часто игрок 2 должен показывать один палец?
Решение. Прежде всего определим стратегии игроков и построим платежную матрицу.
Стратегиями игрока 1 (строки таблицы) являются четыре пары чисел. Первое число каждой пары — это число пальцев, показанное им, второе — число пальцев, которое, как он предполагает, показал его противник. Такие же стратегии имеет игрок 2.
Платежная матрица размером 4 х 4 и другая информация представлены в следующей таблице:
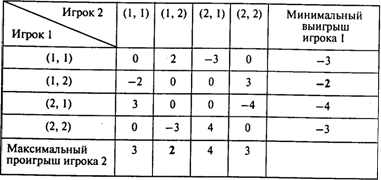
Нижняя цена игры = –2, верхняя цена игры = 2.
Как видим, ¹ , поэтому седловой точки не существует и решение в чистых стратегиях отсутствует. Для решения данной игры построим соответствующую задачу линейного программирования. Для этого сначала преобразуем платежную матрицу таким образом, чтобы все ее элементы были положительными. Максимальное по абсолютной величине значение неположительного элемента платежной матрицы равно 4, поэтому к матрице достаточно прибавить число 5:
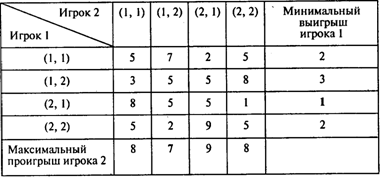
Оптимальная стратегия игрока 1 находится решением следующей задачи линейного программирования [см. (1)]:
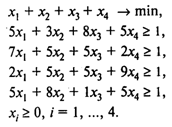
Используя пакет POMWIN, исходную информацию для решения этой задачи можно представить в виде следующей таблицы:
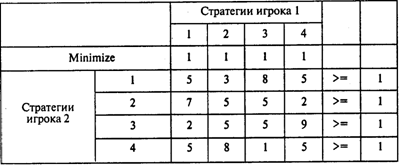
Получаем следующий результат:

Решение (в нижней строке):
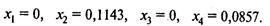
Оптимальное значение целевой функции равно 0,2.
В последнем столбце — двойственные оценки. Переходя к переменным исходной задачи и учитывая, что v = 1/(x1 + х2 + х3 + х4) = 5 и pi = хi v, получаем:
p1 = 0, р2 = 0,5715, p3 = 0, p4 = 0,4285.
Это означает, что при многократном повторении игры первая стратегия (1, 1) и третья стратегия (2,1) игроком 1 не должны использоваться; вторая стратегия (1,2) должна использоваться с частотой 0,5715, четвертая стратегия (2, 2) — с частотой 0,4285.
Аналогично определяем оптимальную стратегию игрока 2:
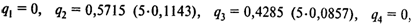
т.е. игрок 2 должен использовать лишь свою вторую стратегию (1,2) с частотой 0,5715 и третью стратегию (2, 1) с частотой 0,4285.
Так как исходная матрица была увеличена на 5, получаем, что цена первоначальной игры равна 0 (5 — 5). Таким образом, исход игры — ничья.
Ответы: 1. Нет, не существует. 2. Ничья. 3. Всегда. 4. 0,572.
Пример 4. Доминирование стратегий.
Платежная матрица для двух игроков имеет вид
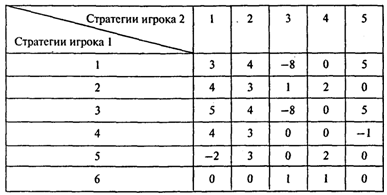
Преобразуйте игру, исключив доминируемые стратегии.
Решение. Для игрока 1: вторая стратегия (строка 2 матрицы) доминирует четвертую и шестую стратегии, поэтому четвертую и шестую строки можно вычеркнуть. Для игрока 2: третья стратегия (столбец 3) доминирует четвертую, поэтому четвертый столбец можно вычеркнуть, и т.д.
Результирующая матрица имеет вид

Пример 5. Как завоевать рынок?
Два конкурирующих друг с другом предприятия, выпускающие стиральные машины, имеют следующие доли общего сбыта своей продукции на местном рынке: 53\% — предприятие 1 и 47\% — предприятие 2.
Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: a1 (b1) — расширить сеть сбыта; a2 (b2) — рекламировать свою продукцию; a3(b3) — увеличить ассортимент (число моделей стиральных машин); a4 (b4) — ничего не предпринимать.
Анализ показал, что при осуществлении обоими предприятиями указанных мероприятий доля (в \%) предприятия 1 на рынке стиральных машин изменится следующим образом:

Сформулируйте данную ситуацию в виде игры.
Вопросы:
1. Какое из мероприятий предприятия 1 наиболее эффективно?
2. Какую долю на рынке будет иметь предприятие 1?
3. Какое из мероприятий предприятия 2 наиболее эффективно?
4. С какой частотой следует предприятию 2 использовать стратегию «реклама»?
Решение. Приведенную выше таблицу можно рассматривать как платежную матрицу игры двух лиц с нулевой суммой. Альтернативы, имеющиеся в распоряжении предприятий, — стратегии игроков. Прежде всего следует исключить доминируемые стратегии игроков: 04 игрока 1 и 64 игрока 2. В результате получим
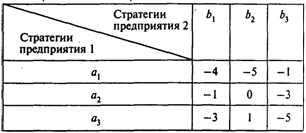
Увеличив все элементы матрицы на 6, решим следующую задачу линейного программирования:
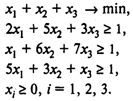
Используя пакет POMWIN, получаем следующий результат:
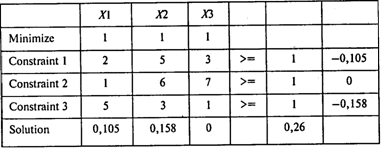
Переходя к переменным исходной задачи и учитывая, что v = 1/(x1 + x2 + х3) = 3,85 и pi = xiv, получаем: р1 = 0,4, р2 = 0,6, p3 = 0, p4 = 0. Цена игры, соответствующая первоначальной матрице, равна –2,15 (3,85 – 6). Таким образом, предприятие 1 при многократном повторении игры должно использовать с частотой 0,4 стратегию а1 (расширить сеть сбыта), с частотой 0,6 — стратегию a2 (рекламировать свою продукцию), а стратегии a3 (увеличить ассортимент) и a4 (ничего не предпринимать) не использовать вовсе. При этом доля сбыта предприятия на рынке уменьшится на 2,15\%. Оптимальная смешанная стратегия предприятия 2: с частотой 0,4 использовать стратегию b1 (расширить сеть сбыта) и с частотой 0,6 — стратегию b3 (увеличить ассортимент). Стратегии a2 (рекламировать свою продукцию) и a4 (ничего не делать) не применять вовсе. Доля предприятия 2 на рынке увеличится на 2,15\%. Казалось бы, поскольку в результате осуществления своих мероприятий предприятие 1 «теряет рынок», ему не следует ничего предпринимать, однако в этом случае оно потеряет еще больше (в соответствии со стратегией a4) из-за действий предприятия 2, которому они выгодны.
Ответы: 1. Реклама. 2. 50,85\%. 3. Увеличение ассортимента. 4. С нулевой частотой, т.е. стратегия «реклама» предприятием 2 вообще не должна применяться.
Вопросы
Вопрос 1. Нижняя цена матричной игры {aij}m,n определяется следующей формулой:
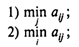
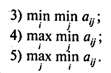
Вопрос 2. Верхняя цена матричной игры {aij}m,n определяется следующей формулой:
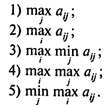
Вопрос 3. Какова верхняя цена следующей игры?
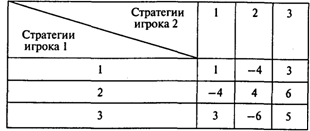
Варианты ответов:
1) 1; 2) 3; 3) 4; 4) 5; 5) 6.
Вопрос 4. Какова нижняя и верхняя цена игры для нижеприведенной матрицы?
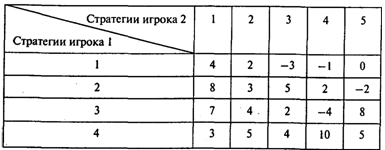
Варианты ответов:
1) (-4, 10); 2) (0, 5); 3) (2, 4); 4) (3, 5); 5) (2, 8).
Вопрос 5. Чему равно значение элемента матрицы игры в седловой точке?
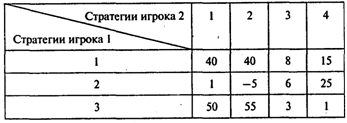
Варианты ответов:
1) 6; 2) 8; 3) 15; 4) 25; 5) седловая точка отсутствует.
Вопрос 6. Используя свойство доминирования стратегий игроков, максимально редуцируйте следующую матрицу игры:
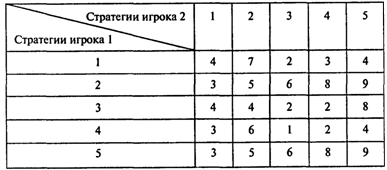
Какова размерность результирующей матрицы?
Варианты ответов:
1)1х2; 2)2х1; 3)2х2; 4)3х2; 5)3х3.
Вопрос 7. Найдите цену следующей игры (без использования пакета POMWIN):

Варианты ответов:
1) 1; 2) 1,5; 3) 2; 4) 2,5; 5) 3.
Вопрос 8. Два игрока одновременно и независимо показывают О, 1, 2 или 3 пальца. Игрок, показавший большее число пальцев, платит другому игроку сумму, равную разности чисел пальцев, показанных им и его соперником. Какова цена такой игры?
Варианты ответов:
1) 3; 2) 2; 3) 1; 4) 0; 5) –1.
Вопрос 9. Два игрока одновременно и независимо показывают 1, 2 или 3 пальца. Пусть s — сумма чисел пальцев, показанных обоими противниками. Если s — нечетное, то игрок 1 платит другому игроку сумму s, если же s — четное, эту сумму выплачивает игрок 2. Чему равна цена такой игры?
Варианты ответов:
1) –1; 2) 0; 3) 1; 4) 1,3; 5) 1,7.
Вопрос 10. Постройте платежную матрицу следующей игры.
Игрок 2 прячет в одном из п мест предмет стоимостью сj (j = 1,.... n). Игрок 1 ищет этот предмет в одном из п мест, и если находит, то получает сj, в противном случае получает 0. Пусть п = 4 и вектор стоимости предметов с = (5, 7, 3, 12). Чему равна цена игры?
Варианты ответов:
1) 1,75; 2) 1,57; 3) 1,32; 4) 1,23; 5) 1,12.
Задачи
Задача 1. По требованию рабочих некоторой компании профсоюз ведет с ее руководством переговоры об организации горячих обедов за счет компании. Профсоюз, представляющий интересы рабочих, добивается того, чтобы обед был как можно более качественным и, следовательно, более дорогим. Руководство компании имеет противоположные интересы. В конце концов стороны договорились о следующем. Профсоюз выбирает одну из шести фирм (Ф1 ¸ Ф6), поставляющих горячее питание, а руководство компании — набор блюд из семи возможных вариантов (B1 ¸ B7). После подписания соглашения профсоюз формирует следующую платежную матрицу, элементы которой представляют стоимость набора блюд:
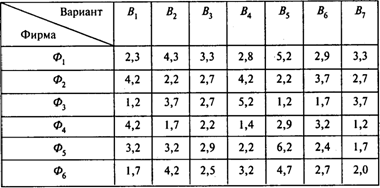
Определите оптимальные стратегии игроков и цену игры.
Вопросы:
1. Чему равна цена игры?
2. Какая фирма наиболее предпочтительна для профсоюза?
3. Какой набор руководство компании считает наиболее «выгодным»?
4. Чему равна нижняя цена игры?
Задача 2. Известный актер обдумывает, где бы ему провести в текущем году отпуск. Он рассматривает шесть возможных вариантов: Монте-Карло (МК), Гавайские острова (Г), Багамские острова (Б), Канарские острова (К), Сочи (С), озеро Байкал (ОБ). Единственный критерий для выбора места отдыха — это стремление избежать встречи с журналистами, которые могут испортить ему отпуск. Если они «выследят» актера, отдых будет испорчен (полезность равна 0). В противном случае все будет, как запланировано (полезность равна 1). Журналисты могут обнаружить актера с такой вероятностью: в Монте-Карло — 0,34; на Гавайских островах — 0,12; на Багамских островах — 0,16; на Канарских островах — 0,4; в Сочи — 0,5; на озере Байкал — 0,2.
Опишите данную ситуацию как игру двух лиц с нулевой суммой (актер — игрок 1). Вычислите цену игры и определите минимаксные стратегии обоих игроков.
Вопросы:
1. Чему равна максимальная ожидаемая полезность отпуска актера?
2. С какой вероятностью актер поедет в отпуск на Байкал?
3. Чему равна верхняя цена игры?
4. В каком из мест наиболее вероятно будет отдыхать актер?
Задача 3. На «Диком Западе» имела место следующая ситуация. Группа из пяти индейцев взяла в осаду лагерь, охраняемый четырьмя белыми. У лагеря два входа: E1 и Е2. Разведчик белых установил, что перед входом Е1 находится как минимум один индеец, а перед входом Е2 — как минимум два индейца. Остальное распределение неизвестно. Командир осажденных может себя и остальных трех человек распределить по E1 и Е2, причем у каждого входа должен быть как минимум один человек. Предполагается, что численно превосходящая (у каждого входа) группа берет в плен всю группу противника без собственных потерь, в то время как при равенстве сил перед каким-либо входом потерь нет с обеих сторон. В качестве платежа (выигрыша) выступает разность числа пленных.
Определите все чистые стратегии обоих противников. Постройте платежную матрицу, считая игроком 1 обороняющуюся сторону. Редуцируйте матрицу, насколько это возможно, и найдите оптимальные стратегии сторон.
Вопросы:
1. С какой частотой белым следует использовать стратегию: расположить по два человека у каждого входа?
2. Кто больше в среднем захватит пленных — белые или индейцы?
3. Какова абсолютная величина разности числа захваченных обеими сторонами пленных?
4. С какой частотой белым следует использовать стратегию:
расположить у первого входа одного, а у второго — трех человек?
5. С какой частотой индейцам следует использовать стратегию:
расположить у первого входа трех, а у второго — двух воинов?
Задача 4. Имеются два предприятия, которые в дополнение к основной продукции могут выпускать побочную продукцию одного и того же назначения — пластмассовые игрушки. Известно, что они могут продавать ее в одном и том же городе. Игрушки немного отличаются по конструкции, оформлению, удобству и т.д. Первое предприятие может выпускать игрушки типа А1, А2,..., Аm; второе — типа B1, В2,..., Bn. Себестоимость и цена игрушек у всех предприятий одинаковы. Всего в течение года продается N игрушек. Если первое предприятие выпускает игрушки типа Аi, а второе — типа Вj, то первое предприятие продаст rijN игрушек, а второе — (N – rijN). Каждое предприятие стремится получить максимальный доход от продажи игрушек.
Пусть т = 4, п = 5, N= 300 000, цена (равновесная) одной игрушки составляет 20 руб., элементы матрицы {rij}4,5 представлены в таблице:
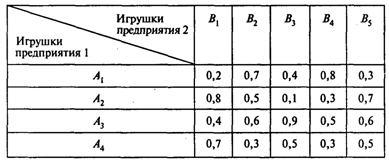
Сформулируйте игру двух лиц, считая игроком 1 первое предприятие. Определите выигрыш (доход от продажи) каждого предприятия.
Вопросы:
1. Каков общий средний доход первого предприятия?
2. Каков общий средний доход второго предприятия?
3. Какое изделие следует выпускать первому предприятию с наибольшей вероятностью?
4. Какое изделие следует выпускать второму предприятию с наибольшей вероятностью?
5. Какова частота применения стратегии «Выпускать изделие B2»?
Задача 5. Сторона В посылает подводную лодку в один из п регионов. Сторона А, располагая т противолодочными кораблями, стремится обнаружить лодку противника. Сторона B стремится этого избежать. Вероятность обнаружения подводной лодки в j-м регионе одним противолодочным кораблем равна рj (j = 1,..., n).
Предполагается, что обнаружение лодки каждым кораблем является независимым событием. Сторона А может посылать в различные регионы разное количество кораблей (распределение т кораблей по регионам и есть ее стратегия).
Пусть т = 3, п = 2, р1 = 0,4, р2 = 0,6.
Считая сторону А игроком 1, построите игру и найдите оптимальное распределение противолодочных кораблей по регионам.
Вопросы:
1. Каков средний выигрыш стороны А?
2. С какой частотой стороне А следует посылать в регион 2 три противолодочных корабля?
3. С какой частотой стороне А следует посылать в регион 1 один противолодочный корабль?
4. С какой частотой стороне В следует посылать подводную лодку в регион 2?
Ответы и решения
Ответы на вопросы: 1—4, 2 — 5, 3—2, 4 — 4, 5—2, 6—3, 7 — 3, 8—4, 9—2, 10—2.
Задача 1. Решение.
Модель линейного программирования и решение представлены в следующей таблице:
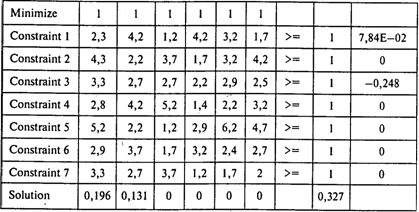
Цена игры v = 1/(0,196 + 0,131) = 3,06.
Вероятности выбора фирм Р = (0,6; 0,4; 0; 0; 0; 0).
Вероятности выбора наборов Q = (0,24; 0; 0,76; 0; 0; 0; 0).
Ответы: 1. 3,06. 2. Ф1. 3. B3 4. 2,3.
Задача 2. Решение.
Матрица игры и решение задачи линейного программирования представлены в следующей таблице:
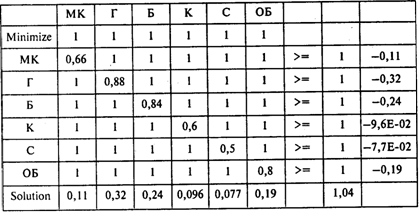
Цена игры равна 0,96. Частоты использования игроком 1 своих стратегий Р = (0,11; 0,32; 0,24; 0,096; 0,077; 0,19).
Ответы: 1. 0,96. 2. 0,19. 3. 1. 4. На Гавайских островах.
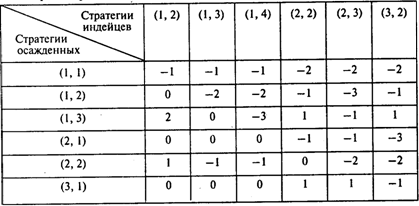
Задача 3. Решение.
Матрица игры имеет вид
После исключения доминируемых стратегий матрица примет вид
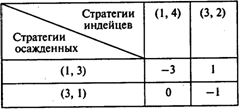
После приведения данной матрицы к положительно определенной, решив задачу, получаем: цена исходной игры равна 0, т.е. белые, даже применяя оптимальную стратегию, теряют на одного человека больше (здесь имеет смысл округлить цену игры до ближайшего целого). Другими словами, индейцы берут в плен на одного человека больше.
Оптимальная смешанная стратегия белых: с частотой 0,2 применять стратегию (1, 3) и с частотой 0,8 — стратегию (3, 1). Оптимальная смешанная стратегия индейцев: с частотой 0,4 применять стратегию (1, 4) и с частотой 0,6 — стратегию (3, 2).
Ответы: 1.0. 2. Индейцы. 3.1. 4.0,2. 5.0,6.
Задача 4. Решение.
Данная игра — это игра двух лиц с ненулевой постоянной суммой. Сумма выигрышей обоих игроков при любых сочетаниях стратегий предприятий равна 6 (все числа в матрице выигрышей даны в миллионах). Сведем ее к игре двух лиц с нулевой суммой. Для этого до игры каждому предприятию выплачивается половина постоянной суммы, т.е. 3, а из выигрыша каждого предприятия (из элементов матрицы) вычитается 3. Полученная матрица соответствует игре с нулевой суммой, поэтому достаточно указать в ней только выигрыши одного (первого) предприятия. После необходимых расчетов матрица игры имеет вид

Прибавим к матрице число 3, чтобы все ее элементы были положительными. Матрица задачи и решение показаны в следующей таблице:
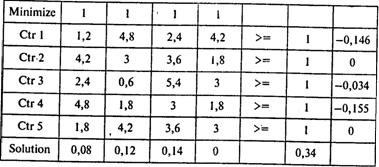
Цена преобразованной игры равна 1/0,34 = 2,94.
Оптимальная смешанная стратегия игрока 1 (частоты использования игроком 1 своих стратегий) Р = (0,23; 0,36; 0,41; 0).
Для игрока 2 оптимальная смешанная стратегия Q = (0,43; 0; 0,1; 0,47; 0). Цена исходной игры с нулевой суммой равна —0,06. Поскольку оба игрока получили по 3 млн руб., общий доход первого предприятия составляет 2,94 млн руб., доход второго предприятия равен 3,06 млн руб.
Ответы: 1. 2,94 млн руб. 2. 3,06 млн руб. 3. Изделие А3 4. Изделие B4 5. Частота применения стратегии «Выпускать изделие B2» равна нулю.
Задача 5. Решение.
Стратегии игрока 2: I — послать подводную лодку в регион 1; II — послать подводную лодку в регион 2. Множество стратегий игрока 1: {(0, 3), (1, 2), (2,1), (3, 0)}. Числа в скобках — это количество противолодочных кораблей, посылаемых в каждый из двух регионов.
Вероятность обнаружить подводную лодку в регионе j с помощью k противолодочных кораблей равна (1 – (1 – рj)k). Предположим, что выигрыш игрока 1 равен единице в случае обнаружения подводной лодки и нулю — в противном случае. Тогда матрица игры имеет вид

Элементы матрицы — средние выигрыши игрока 1 в соответствующих ситуациях.
Модель линейного программирования и решение (элементы матрицы увеличены на 1):
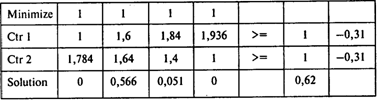
Цена игры равна 1/0,62 = 1,61. Цена первоначальной игры равна 1,61 – 1 = =0,61.
Частоты применения стороной А своих стратегий Р = (0; 0,92; 0,08; 0). Сторона В посылает подводную лодку в оба региона с равной вероятностью (0,31×1,61 = 0,5).
Ответы: 1. 0,61, т.е. средний выигрыш равен цене игры.
2. Стороне А не следует посылать в регион 2 три противолодочных корабля.
3. С частотой 0,92.
4. С частотой 0,5.
Обсуждение Исследование операций в экономике: модели, задачи, решения
Комментарии, рецензии и отзывы
