3. временная стоимость денег
3. временная стоимость денег
Управление финансовыми активами, например акциями и облигациями, предполагает оценку (valuation) потоков денежных средств, ожидаемых в результате использования этих активов. Фундаментальным принципом, значение которого было осознано, наверное, вскоре после появления самих денег, является принцип их временной неравноценности: деньги, которыми мы обладаем в разные моменты времени, имеют неодинаковую ценность. Временная ценность денег (time-value of
168
money) играет не меньшую роль, чем сами размеры денежных сумм: «Время деньги!» Рубль сегодня имеет большую ценность, чем рубль, который должен или может быть получен спустя некоторое время, поскольку его можно вложить (инвестировать) в финансовые и имущественные активы с надеждой получения в будущем дополнительного дохода. Процесс оценки будущих денежных потоков называется анализом дисконтированного денежного потока (ДДП), а так как все финансовые решения основаны на оценках будущих денежных потоков, анализ ДДП играет исключительно важную роль. Другое, часто применяемое его название метод капитализации доходов.
Любое учреждение, будь то производственная фирма (компания, корпорация и т.д.) или государство, в которые мы добровольно или принудительно (как в случае с государством) вкладываем деньги, с точки зрения теории финансов представляет собой не более чем аппарат или станок для производства будущего потока денежных выплат, идет ли речь о «Дженерал моторе», империи Билла Гейтса или китайской прачечной. В аппарат закладывается начальная сумма Р (принципал), на выходе из него получается поток денежных выплат CF (cash flow). От свойств «аппарата» зависит величина потока CF, получаемая на выходе при одной и той же начальной (входной) величине Р. Но какова бы ни была величина CF, она будет получена только через период времени t(CF). Согласно принципу временной ценности денег, для приведения ее к настоящему моменту (t = 0) моменту «закладывания» начальной суммы Р в аппарат она должна быть дисконтирована, т.е. уменьшена в (1 + к) раз на дисконтирующий множитель (1 + к):

Стоимости PV и параметру k (ставке дисконтированияdiscount rate) также приписан значок t по указанной выше причине. PVt называется текущей, или приведенной стоимостью (current, present
value); к означает процентную ставку (interest rate), которая будет минимальной, если ее обеспечивает самый надежный аппарат солидный банк. Положив в него деньги, мы ничем не рискуем, но и ставка при этом будет самой низкой. С ростом риска или, как говорят, неопределенности (uncertainty) получения дохода на вложенный капитал должна увеличиваться ставка. Таким образом, начальную сумму (принципал) Р следует сравнивать не с выходящим из аппарата потоком CFt, а с приведенной стоимостью PVt в этом и состоит основной принцип анализа дисконтированного денежного потока
(ДДП).
На этой схеме и в формуле (2) Vo текущая, или приведенная стоимость актива, иногда называемая еще истинной (intrinsic, true); CFt ожидаемые денежные поступления (приток или отток inflow,
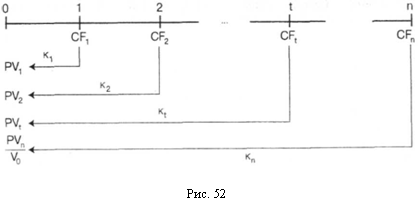 |
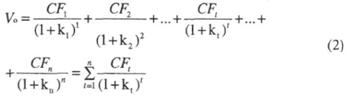
outflow) в момент t, зависящие от допускаемого риска, иначе говоря, неопределенные (uncertain); к -процентная ставка, которую, в зависимости от контекста, называют требуемой доходностью (required earnings), или стоимостью капитала, она устанавливается с учетом риска, связанного с потоком CFt в период t; n число периодов, в течение которых ожидается поступление денежных средств (cash flow).
Приведенная стоимость (2) зависит от потоков CFt, kt и числа периодов п. Чтобы поближе с ней познакомиться, положим все потоки одинаковыми и равными С и все ставки равными к. Тогда сумма вычисляется по формуле геометрической прогрессии со знаменателем х = 1/(1 + к):
V — С • А(п, к), А(п, к) = 1 (1 + к)-"/к.
(3)
(Напомним эту формулу:
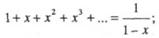
справедливость ее становится очевидной, как только мы умножим левую часть (бесконечный ряд) на знаменатель правой части: умножение на 1 даст тот же ряд, а умножение на (-х) даст тот же ряд, но уже без единицы, который должен вычитаться из предыдущего, так что в результате слева остается только 1, т.е. получается тождество.)
Величина А(п, к) называется коэффициентом приведения годовой ренты. Руководства по финансовым расчетам, как правило, содержат таблицы, позволяющие подсчитать V при заданных С, к и п. Однако они более полезны при решении обратной и чаще встречающейся задачи: по заданным V, С и п определить процентную ставку к. Так поступают часто потому, что хотя уравнение (2) и является простым алгебраическим, однако оно не решается «в лоб» относительно интересующего нас параметра ставки дисконтирования к.
Полезно отметить важный частный случай формулы (1), когда все потоки С и ставки к одинаковы, а число членов п бесконечно (n = ос). Тогда сумма членов бесконечной геометрической прогрессии перестает зависеть от п и выражение для А(п, к) сильно упрощается:
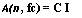 1—г = А(«Д)=-. Ы tt + Jt) *
1—г = А(«Д)=-. Ы tt + Jt) *
(4)
Облигации (bond) относятся к финансовым инструментам с гарантированным, определенным (certain, determined) доходом, задаваемым процентной ставкой (interest rate) i. Поэтому полный дисконтированный доход по ним рассчитывается по тем же формулам, что и для обыкновенных акций в модели нулевого роста, если заменить в них ожидаемую (expected), неопределенную (uncertain) ставку к на гарантированный процент i. Этот процент зависит от эмитента (корпорация, государство, муниципальные власти). Некоторые иллюстративные материалы, относящиеся к акциям и облигациям США приведены в табл. 33.
Та блица 33
Некоторые характеристики ценных бумаг американских компаний. Средняя годовая доходность и ИПЦ (в
\%)
| Годы | Казна- | Долгосрочные | Долгосрочные | Обыкновен- | Изменение |
| чейские | государственные | облигации | ные акции | индекса | |
| векселя | облигации | корпорации | потребительских цен | ||
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1926 | 3,26 | 7,77 | 7,37 | 11,62 | -1,49 |
| 1927 | 3,12 | 8,93 | 7,44 | 37,49 | -2,08 |
| 1928 | 3,56 | 0,10 | 2,84 | 43,61 | -0,97 |
| 1929 | 4,75 | 3,42 | 3,27 | -8,42 | 0,20 |
| 1930 | 2,41 | 4,66 | 7,98 | -24,90 | -6,03 |
| 1931 | 1,07 | -5,31 | -1,75 | —43,34 | -9,52 |
| 1932 | 0,96 | 16,84 | 10,82 | -8,19 | -10,30 |
| 1933 | 0,30 | 0,07 | 10,38 | 53,99 | 0,51 |
| 1934 | 0,16 | 10,03 | 13,84 | —1,44 | 2,03 |
| 1935 | 0,17 | 4,98 | 9,61 | 47,67 | 2,99 |
| 1936 | 0,18 | 7,52 | 6,74 | 33,92 | 1,21 |
| 1937 | 0,31 | 0,23 | 2,75 | -35,03 | 3,10 |
| 1936 | -0,02 | 5,53 | 6,13 | 31,12 | -2,78 |
| 1939 | 0,02 | 5,94 | 3,97 | -0,31 | -0,48 |
| 1940 | 0,00 | 6.09 | 3,39 | -9,78 | 0,96 |
| 1941 | 0,06 | 0,93 | 2,73 | -11,59 | 9,72 |
| 1942 | 0,27 | 3,22 | 2,60 | 20,34 | 9,29 |
| 1943 | 0,35 | 2,08 | 2,83 | 25,90 | 3,16 |
| 1944 | 0,33 | 2,81 | 4,73 | 19,75 | 2,11 |
| 1945 | 0,33 | 10,73 | 4,08 | 36,44 | 2,25 |
| 1946 | 0,35 | -0,10 | 1,72 | -8,07 | 18,16 |
| 1947 | 0,50 | -2,62 | -2,34 | 5,71 | 9,01 |
| 1948 | 0,81 | 3,40 | 4,14 | 5,50 | 2,71 |
| 1949 | 1.10 | 6,45 | 3,31 | 18,79 | -1,80 |
| 1950 | 1,20 | 0,06 | 2,12 | 31,71 | 5,79 |
| 1951 | 1,49 | -3,93 | -2,69 | 24,02 | 5,87 |
| 1952 | 1,66 | 1,16 | 3,52 | 18,37 | 0,88 |
| 1953 | 1,82 | 3,64 | 3,41 | -0,99 | 0,62 |
| 1954 | 0,86 | 7,19 | 5,39 | 52,62 | 0,50 |
| 1955 | 1,57 | -1,29 | 0,48 | 31,56 | 0,37 |
| 1956 | 246 | -5,59 | -6,81 | 6,56 | 2,86 |
| 1957 | 3,14 | 7,46 | 8,71 | -10,78 | 3,02 |
| 1958 | 1,54 | -6,09 | -2,22 | 43,36 | 1,76 |
| 1959 | 2,95 | -2,26 | -0,97 | 11,96 | 1,50 |
| 1960 | 2,66 | 13,78 | 9,07 | 0,47 | 1,48 |
| 1961 | 2,13 | 0,97 | -1,29 | 26,89 | 0,67 |
| 1962 | 2,73 | 6,69 | 7,95 | -8,73 | 1,22 |
| 1963 | 3,12 | 1,21 | 2,19 | 22,80 | 1,65 |
| 1964 | 3,54 | 3,51 | 4,77 | 16,48 | 1,19 |
| 1965 | 3,93 | 0,71 | -0,46 | 12,45 | 1,92 |
| 1966 | 4,76 | 3,65 | 0,20 | -10,06 | 3,35 |
| 1967 | 4,21 | -9,18 | -4,85 | 23,98 | 3,04 |
| 1966 | 5,21 | -0,26 | 2,57 | 11,06 | 4,72 |
| 1969 | 6,58 | -5,07 |
|||
