10.4. модели расширяющейся экономики
10.4. модели расширяющейся экономики
Описания экономической динамики, в которых технологические возможности и целевые установки неизменны во времени, относятся к моделям расширяющейся экономики. Основным методом их исследования является изучение стационарных траекторий, или траекторий сбалансированного роста. Первоначально анализ стационарного роста развивался по двум независимым направлениям:
в однои двухпродуктовых моделях, в которых технологические возможности описывались производственной функцией;
в многопродуктовой линейной модели, построенной и исследованной Дж. Фон Нейманом.
Модель Неймана включает п продуктов и т способов их производства. Каждым способом при единичной его интенсивности в течение единичного интервала времени производится набор продуктов bj = (bjy,b^j). При этом затрачивается набор продуктов dj = (a^j,a^j),] є 1: т. Все способы могут применяться с любыми неотрицательными интенсивностями. Из п-мерных векторов-столбцов аи bj составляются матрицы затрат А = (а,у) и выпуска В = (by). Модель Неймана позволяет учесть непроизводственное потребление только в неявной форме. Элементы матрицы затрат А могут включать часть, направляемую на потребление, например, А = А' + С, где a'j — собственно технологические затраты, а су — векторы потребления на единицу интенсивности способа j. Векторы Cjг составляют матрицу С.
Траекторией (планом), выходящей из точки у0 = В ■ zv называется последовательность m-мерных векторов интенсивности {zt}, t є 1: Т, удовлетворяющих балансовым уравнениям
AzM<Bzt, zt>0, ґеО:(Г-1).
При интенсивностях zt непроизводственное потребление в интервале t составляет С ■ zt.
Стационарной траекторией, или траекторией сбалансированного роста, называется такая последовательность zv что zt = а( ■ z, где z — m-мерный вектор, а а — положительное число. На стационарной траектории неизменны пропорции использования способов затрат и выпуска, экономика растет с постоянным темпом а. Темп а и пропорции z должны удовлетворять условиям
a-Az<Bz, zZQ, z*0.
Особый интерес представляет стационарная траектория, которой соответствует наибольший темп — максимальный темп технологического роста. Его можно найти из решения задачи математического программирования: а -» max. Вектор z, на котором достигается максимум, называется неймановским.
Системе балансовых соотношений сопоставляется двойственная ей система ценностных соотношений
prA>pt+i-B, ptZ0, pf*0,
показывающая, что ценность выпуска не превосходит ценности затрат. Траектория оценок pt такая, что pt p~f • р, называется стационарной. Для нее $р-А>рВ, р£0,р*0.
Оценки р*, удовлетворяющие этим условиям при минимальном р, называются неймановскими ценами. Если модель экономики неразложима, т. е. для производства любого продукта прямо или косвенно используются все продукты, то справедлива теорема двойственности: таха тіпр а0. При этом неймановские цены стимулируют неймановскую траекторию роста:
а0 р* AzZp* Bz
для Bcexz £ 0, причем а0 р' A-z* =р* Bz*.
Другим примером расширяющейся экономики являются одно-продуктовые модели с линейно однородными производственными функциями. Примером однопродуктовой модели долговременного экономического роста является модель Рамсея. В ней поток национального дохода создается имеющимися в данный момент производственными фондами и используемыми трудовыми ресурсами. Этот поток делится на потребляемую и накапливаемую части. Последняя определяет прирост производственных фондов, т. е.
F(K,L) = C + K',
где К' — наличные производственные фонды, С — интенсивность потребления, I — используемые трудовые ресурсы. Все показатели относятся к моменту времени г. Производственная функция F не меняется со временем, т. е. технический прогресс отсутствует.
Английский экономист Ф. П. Рамсей поставил вопрос о том, какую часть национального дохода общество должно сберегать в целях накопления, и тем самым впервые сформулировал задачу планирования экономического роста как оптимизационную. Ее целевая функция определялась как интегральная полезность за время существования экономической системы; полезность в каждый момент равнялась разности между уровнем удовлетворения потребностей ЩС) и «бременем труда» V(L)). При этом для упрощения было принято, что численность населения не меняется, вклад в целевую функцию потребления в различные моменты времени рассматривается с одинаковым весом, т. е. дисконт равен 1. Очевидно, что интегральная полезность за период (0, °°) окажется бесконечной и выбор рациональной политики сбережений будет невозможен. Чтобы преодолеть эту трудность, Рамсей допускал, что функции F, U, V предполагают достижение максимального уровня полезности в некоторой момент — уровня «блаженства». Теперь можно было бы перейти от максимизации интегральной полезности к минимизации неудовлетворенной потребности:
ее
j(B-U(C) + V(L))dt-+mn. о
Задача отыскания К, I, С при заданном К0 представляет собой модель Рамсея. Рамсей показал, что произведение сбережений на предельную полезность потребления равно в каждый момент времени объему неудовлетворенной потребности (закон Кейнса — Рамсея), т. е.
F(K,L)-C)U'(C)-В-(U(C) -V(L).
dF
Анализ модели показал, что V'(L) = U'(C)—, т. е. предельное
аК
«бремя труда» равно произведению его предельной производительности и предельной полезности потребления, а также
U"(C) = U'(C)¥-,
т. е. предельная производительность производственных фондов
dF
— равна темпу изменения предельной полезности. Отметим, что аК
норма накопления, по Рамсею, оказывается чрезмерно высокой.
В однопродуктовых моделях стационарные траектории, т. е. пропорциональный рост производственных фондов, занятости и потребления называют золотым веком, а правило распределения национального дохода на потребление и накопление, обеспечивающее максимальное душевое потребление, золотым правилом накопления. Это правило характеризуется распределением национального дохода на потребление и накопление в постоянной пропорции. Понятие «золотое правило» было введено при анализе однопродуктовых моделей экономической динамики с линейно однородными производственными функциями. Рассмотрим такую модель.
Пусть Kt и Lt — производственные фонды и трудовые ресурсы, используемые в единичном интервале (году) г. Произведенный в этом интервале национальный доход Nt определяется функцией F двух аргументов: Nt =F(Kt,Lt).
Производственная функция F называется линейно однородной, если
F(XK,XL) = ^(K,L) для всех Х>0 и K,L>0.
Пусть также 1-А. — коэффициент выбытия производственных фондов в течение единичного интервала времени, It и Ct — объемы инвестиций в производственные фонды и потребления в году г. Простейшая модель динамики задается соотношениями:
Nt=F(Kt,Lt), Nt=Ct+Itl Kt+1=vKt+It, tsO-.T.
Динамика трудовых ресурсов считается заданной; последовательность {Kt,Nt,It,Ct}, гєО: Т называется траекторией. Если трудовые ресурсы растут с постоянным темпом р > 1, т. е. Lf = L ■ pf, то «золотым веком», или состоянием «золотого века» называются траектории сбалансированного роста, на которых все экономические показатели растут с постоянным темпом р, а пропорции распределения национального дохода неизменны. При этом доля накопления
I К St=—, фондовооруженность kt= — и душевое потребление
Ct
ct = — постоянны. Такие траектории называются также стационарными. При стационарном росте Kt=Kpt, Nt=N-pt, Ct=Cpt и It=Ipt модель можно рассматривать как пример моделей расширяющейся экономики.
Воспользовавшись линейной однородностью, национальный доход на душу населения при фондовооруженности kt обозначим
(к л f(kA) = F -Ці
В «золотом веке» фондовооруженность и душевое потребление связаны соотношением с = f{k) (р v) • к.
Золотое правило накопления заключается в выборе такой его доли 5* в национальном доходе, которая обеспечивает максимальное душевое потребление на траекториях «золотого века». Т. к. с максимально при к', удовлетворяющем уравнению f'{k) = p-v, то
5-_(р-у)-fc'
Золотое правило накопления обеспечивает равенство чистой «предельной эффективности» производственных фондов f'{k) = р V темпу прироста экономики р 1. Если в начальном состоянии
^0 7 7 *
— = *с0 * к, то применение золотого правила на каждом шаге при-^°
ведет к построению траектории, для которой kt -»к*.
Глубокое обобщение этих результатов на многосекторные модели с учетом потребления в явном виде было получено Д. Гейлом. Сформулируем сначала модель Гейла в упрощенном виде. Как и модель Неймана, она включает п продуктов и т способов их производства и описывается парой матриц затрат А и выпуска В продуктов. Кроме того, каждый способ j требует затрат труда lt при единичной интенсивности, j є 1 : т. Если z m-мерный вектор интенсивностей, то затраты и выпуск продукции равны А • гнВ • z соответственно, а затраты труда (I, г), где I (/,,...,/„).
Пусть It — наличие трудовых ресурсов в интервале (г, г + 1), а с, п-мерный вектор потребления в этом интервале. Траекторией называется последовательность {zv ct}, t є 0 : (Г 1), удовлетворяющая балансовым ограничениям по продуктам и труду
A-zt+1<,B-zt-ct, I-zt<Lt; ztr>0, ctr>0, teO:(r-l).
Эту модель можно изучать как расширяющуюся экономику, если
трудовые ресурсы растут с постоянным темпом Ц = L-p*. В этом
случае стационарной называется траектория, на которой zt = L ■ р( ■ г,
Сі=Ь-р1-с.
Ее также называют траекторией сбалансированного роста. Векторы z и с определяют интенсивности и потребление на одного работающего и удовлетворяют соотношениям
p-AzuBz-c, l-zu) ztQ, cZO.
Предпочтения на множестве стационарных траекторий задаются функцией полезности и, зависящей от объема годового душевого потребления. Оптимальной называется стационарная траектория, для которой z , с максимизируют и(с).
Стационарной оптимальной траектории модели двойственна стационарная траектория оценок pt р"' • р, oot р~' • со. Стационарные оценки продуктов р и труда to удовлетворяют соотношениям рЪ.ис), р,£и/(с*), если с* >0, р ■ В £ р • р • А + to ■ I, p-Bj =ppAj +со-1у,если Zj >0.
Исследование стационарных траекторий является мощным и традиционным инструментом экономического анализа. Например, модель Неймана позволяет в различных предположениях о связи потребления с производством оценить технологически достижимый максимальный темп роста экономики и необходимую для этого отраслевую структуру. Анализ стационарных моделей роста показывает, что двойственные оценки со временем снижаются. Из модели Іейла следует, что темп роста определяется динамикой лимитирующего ресурса. Двойственного соотношения показывают, что при постоянных ценах ценность произведенной продукции складывается из материальных затрат р • Aj, затрат труда ш • lj и платы за фонды (Р 1) • Р ■ Аґ
Гипотеза стационарности оправдана, когда оптимальные траектории близки к стационарным, т. е. к магистралям. Теорема о магистрали доказана для ряда моделей расширяющейся экономики. Для модели Неймана с линейной терминальной целевой функцией u(z1,...,zT) = f(zT) = pTzT теорема утверждает, что пропорции оптимальных интенсивностей и цен близки к неймановскому виду, исключая, быть может, некоторые отрезки времени в начале и конце планового периода. Суммарная длительность этих отрезков не зависит от продолжительности планового периода. Она верна в предположениях положительности вектора начальных условий у0 и некоторых предположениях о матрицах Л и В, из которых наиболее существенными являются требования единственности неймановских интенсивностей и цен z*,p* и положительности последних.
Модель Гейла после перехода к душевым показателям имеет следующий общий вид:
Г-1
£ u(c,)-> max, t=o
при условиях (xt,yt)eQ, xM<>yt-ct, £єО:(Г-1).
Рассмотренный выше ее частный случай сводится к этому виду, если положить Q = {(x,y)x = Az, у = Bz, lz£l, z£0}. Оптимальная стационарная траектория х у*, с модели находится как решение задачи и (с) -> max, при условиях (х, у) є Q,xuy-c.B предположениях продуктивности, усиленных требований к выпуклости Q и вогнутости и, а также некоторых дополнительных технических требований для оптимальных траекторий, исходящих из у0 > 0, верна слабая теорема о магистрали: число моментов времени t, когда элементы оптимальной траектории х,у,с заметно отличаются от х*, у*, с, ограничено и не зависит от Т. Сильная теорема о магистрали, когда такие моменты встречаются лишь в начале и конце планового периода (ее называют иногда теоремой о средней магистрали) доказывается в более жестких предположениях.
В моделях с бесконечным плановым периодом Т оо наряду с оптимальными траекториями изучаются хорошие траектории. Тра
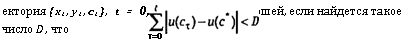 для t = 1, 2,т. е. на хороших траекториях потери суммарной полезности в сравнении с ее значениями на траектории оптимального сбалансированного роста равномерно ограничены при всех t. Они существуют, если у0 > 0. Множество хороших траекторий содержит оптимальные траектории, если последние существуют. Для хороших Траекторий ИМЄЄТ МеСТО (x't,y't ,Ct )~>(Х*, У, С*) При t -» оо.
для t = 1, 2,т. е. на хороших траекториях потери суммарной полезности в сравнении с ее значениями на траектории оптимального сбалансированного роста равномерно ограничены при всех t. Они существуют, если у0 > 0. Множество хороших траекторий содержит оптимальные траектории, если последние существуют. Для хороших Траекторий ИМЄЄТ МеСТО (x't,y't ,Ct )~>(Х*, У, С*) При t -» оо.
Это утверждение называют иногда теоремой о поздней магистрали.
10.5. Теории и модели экономического иикла
Модели экономического цикла рассматривают регулярные колебания деловой активности.
Современная трактовка экономического цикла, свойственная большинству экономистов, характеризуется несколькими предположениями, без учета которых невозможно правильно оценить состояние исследования в данной области:
Экономический цикл — это единый процесс, последовательно проходящий через фазы кризисов и подъемов. Предметом исследования является весь цикл, а не его отдельные фазы.
Цикл — процесс многокомпонентный. Общее движение «деловой активности» складывается как сумма нескольких составляющих, колебания которых могут существенно отличаться по фазе, амплитуде и продолжительности.
Цикл — это колебание, происходящее вокруг трендовой траектории хозяйственного роста, причем в значительной мере независимо от последнего.
Циклические колебания трактуются как колебания, происходящие вокруг положения равновесия.
Циклические колебания тесно увязываются с вопросами государственно-монополистического регулирования.
В теориях цикла можно выделить два направления: неокейнси-анское и неоклассическое. Рассмотрим основные черты, характеризующие эти направления, а также некоторые модели.
В центре кейнсианской теории — факторы, определяющие уровень и динамику национального дохода, а также уровень занятости. Эти факторы Кейнс рассматривал на основе формирования так называемого эффективного спроса, главным компонентом которого являются расходы на личное потребление С и инвестиции /, рассматриваемые как эндогенные переменные, и государственные расходы G, являющиеся экзогенной переменной. Кейнс и его последователи определили целый ряд функциональных зависимостей, характеризующих динамику потребления, инвестиций и национального дохода в целом. Потребительская функция, по Кейнсу, зависит от уровня дохода: чем выше доход, тем меньше общество склонно увеличивать потребление, тем большую его долю оно сберегает. Инвестиции, которые должны поглощать эти сбережения, определяются ожидаемой выгодой от инвестиций и описываются инвестиционной функцией, предел которой равен норме процента. Особенно большое значение Кейнс придавал динамике процентной ставки, ее зависимости от денежного спроса, спекуляции на денежных рынках и субъективных факторов, определяющих состояние этих рынков. Функция денежного спроса в теории Кейнса определяется двумя главными параметрами:
увеличением дохода, способствующим росту числа и масштабов сделок (трансакционный спрос);
колебаниями процентных ставок, отражающим спекулятивный спрос.
В простейшей форме кейнсианская модель определения национального дохода может быть выражена системой уравнений. Основные переменные в ней:
Y — национальный доход;
С — потребление;
/ — инвестиции;
R — процентные ставки (эндогенные макропеременные); G — государственные закупки;
М — денежное предложение (экзогенные переменные); Р — уровень цен (условно-постоянная величина).
В этих обозначениях основные параметры кейнсианской модели имеют вид:
уровень дохода У-C + J+G;
потребительский спрос С а + b(l -1) • У;
инвестиционный спрос I е + d • R;
денежный спросМ(к • Y-h -R)Р.
Здесь а, Ь, е, d, к, h — постоянные, определяемые на основе статистики, a t — время.
Важное место в кейнсианской теории принадлежит концепции мультипликатора, характеризующей соотношение между приростом инвестиций и приростом национального дохода. По Кейнсу, расходы на инвестиции (или государственные расходы) превращаются в первичные доходы, затем часть из. них, расходуясь, превращается во вторичные, третичные доходы и т. п. Одновременно увеличивается и занятость, и объем производства. Общий эффект мультипликативного процесса, так же как и значение мультипликатора, зависят от того, в каких долях доход разделяется на потребляемую и сберегаемую части. Чем большая часть дохода потребляется, тем больше дохода будет приносить первоначально инвестированная сумма денег, тем выше конечная сумма прироста дохода.
Если AY — первоначальный прирост дохода (равный приросту инвестиций), а потребляемая доля этого прироста, или предельная склонность к потреблению, составляет Ь, то можно получить следующий ряд, выражающий сумму оборота дохода:
AY = AI + b-AI + b*AI + b3 А1 + ... + Ъп-А1 = А1—,
1
где ДУ — прирост национального дохода, ^—— мультипликатор,
выражаемый через предельную склонность к потреблению Ь. Чем выше склонность к потреблению, тем больше мультипликатор, и наоборот.
Теория мультипликатора Кейнса связала приросты национального дохода и личного потребления вследствие инвестиций (или государственных расходов). Эта модель, дополненная впоследствии обратной связью между приростом дохода и инвестициями, стала составной частью всех кейнсианских моделей цикла.
В качестве фундаментальной причины цикла представители неокейнсианской концепции рассматривают процесс приспособления накопленного капитала к размерам производства, которые, в свою очередь, сами постоянно меняются под воздействием и в ходе этого приспособления. Предполагается, что между объемом ежегодно воспроизводимой стоимости — потоком, с одной стороны, и ее накопленным к данному моменту запасом — с другой, существует некая нормальная, или равновесная, пропорция. При прочих равных условиях, чем больше ежегодный объем производства, тем больше должен быть и объем накопленного капитала. Обычно эта связь представляется нежесткой, не как технологически заданная постоянная, а только как средняя, доминирующая, в конечном счете, как тенденция. Пока равновесная пропорция не нарушена, циклических колебаний нет, если же они происходят, это означает, что пропорция поток/запас отклоняется то в одну, то в другую сторону от равновесной величины. При этом колебания капитала и производства взаимосвязаны. Маневрирование капиталом преследует постоянно ускользающую цель — достичь нормальной величины относительно размеров ежегодного производства. Последнее же не остается на постоянном уровне, и под влиянием изменений в скорости накопления (в ходе маневрирования капиталом) оно тоже колеблется.
В соответствии с описанными представлениями центральное место занимает анализ движения двух показателей: капитала и дохода. В качестве конечного дохода Y различают три главных компонента Y-C + I + A, где С — фазовые (т. е. зависящие от фазы цикла) потребительские расходы; I — расходы на инвестиции; А — автономные расходы, часть реальных инвестиций, которая не зависит от уровня и изменений национального дохода, а зависит от конкурентных факторов, таких как модернизация производства с целью снижения затрат или использования преимуществ, даваемых новым изобретением.
В большинстве неокейнсианских моделей описание цикла сводится к описанию поведения трех компонентов расходов. При этом роль каждого компонента в колебательном механизме далеко не одинакова.
Наименьшее внимание уделяется автономным расходам. Обычно предполагается, что их величина складывается из тех частей потребительских и инвестиционных затрат, которые не связаны с фазой цикла и определяются долговременными факторами.
Величина фазового потребления в простейших версиях неокейн-сианских моделей задается как постоянная доля от прошлых расходов. Пропорция между доходом и потреблением связана с понятием мультипликатора, однако, в конечном счете, действительная роль закономерностей потребления, как и мультипликационных процессов в неокейнсианских моделях цикла, невелика. Главное внимание уделяется способу задания фазовых инвестиционных расходов, определяющих, в свою очередь, поведение капитала — другого ключевого показателя в неокейнсианских моделях. Исходной причиной, приводящей в действие весь циклический механизм, является стремление предпринимателей привести фактический объем капитала к равновесному уровню. В построениях неокейнсианцев этот уровень — не просто расчетная величина, но в каком-то смысле лучшая из всех возможных на данный момент оптимальная. Поэтому здесь она называется желаемой.
Конкретно способ изменения капитала, задаваемый в моделях рассматриваемого типа, основывается на двух постулатах. Первый гласит, что в каждый момент времени существует желаемая величина основного капитала К. Согласно второму постулату, направление изменения фактического капитала определяется в зависимости от его разрыва с желаемым:
если желаемый уровень превышает фактический, то последний начинает возрастать;
при совпадении желаемой и фактической величин чистые инвестиции равны нулю и капитал не изменяется;
если же желаемый уровень превышен, то чистые инвестиции становятся отрицательными (дезинвестирование), и капитал уменьшается.
Наибольшее распространение получили инвестиционные функции, которые строились в соответствии с принципом акселерации. В простейшем виде постулируемая связь имеет вид
Jt=a0t-i-*t-2)Здесь фазовые инвестиции в год t предполагаются равными чистым инвестициям. Постоянный коэффициент ос, называемый акселеК
ратором, есть величина желаемой капиталоемкости а=~ •
Формулировка принципа акселерации сочетается обычно с ограничениями на инвестиции. Ограничение сверху в явном виде использовано в модели Гудвина и ассоциируется с наличными производственными мощностями в инвестиционных отраслях.
Модель Гудвина является одной из наиболее простых моделей экономического цикла. Она задается следующими соотношениями:
Yt=Ct+It+At, Ct =b-Yt_lr
It=Kt-Kt =
Pt,Kt>Kt_1,Pt>0, pt,K<Kt_lrPt <0,
где Y— конечный доход; С— потребительские расходы; І— расходы на чистые инвестиции; А — автономные расходы; К, К — соответственно, фактический и желаемый основной капитал; Р, р — соответственно, верхний и нижний пределы для чистых инвестиций. Значения этих величин связаны, с одной стороны, с мощностью инвестиционных отраслей, а с другой — с ежегодным потреблением капитала. Потребление капитала — сумма начисленной амортизации фирм в течение данного года.
Колебания в модели Гудвина выводятся из периодического изменения соотношения между фактическим и желаемым уровнем капитала. Когда желаемый уровень капитала больше фактического, чистые инвестиции положительны и продолжается циклический подъем. Когда фактический капитал превышает желаемый (оптимальный), инвестиции становятся отрицательными и начинается кризис, который будет длиться до тех пор, пока потребление фактического капитала не сократит его уровень ниже желаемого.
Модель можно сильно изменить, введя дополнительные лаги, задав плавный переход от одного крайнего значения инвестиций к другому, но суть ее останется той же, пока действует первый регулятор.
Наиболее известным и исследованным является тот вариант теории цикла, который описывается моделью мультипликационно-ак-селерационного взаимодействия (МА-моделью). В простейшей модели такого типа присутствуют уравнения, описывающие формирование дохода из расходов и динамику его активных компонентов, например:
Yt"Ct+It+At, Ct=b-Yt.„
^"«(П-і-П-г).
Главные свойства этих моделей:
Если автономные расходы растут постоянными трендовыми темпами, то среди решений модели существует траектория равномерного роста дохода (и одновременно потребления и инвестиций) теми же темпами.
Если под влиянием каких-либо факторов экономика сошла с равновесной траектории роста, то характер ее дальнейшего движения определяется коэффициентами МА-модели. При некотором их сочетании происходят колебания вокруг равновесной траектории.
3. Если акселератор равен единице, амплитуда колебаний остается
постоянной. При меньшем (большем) акселераторе происходит
постепенное затухание (увеличение) размаха колебаний.
Одна из основных проблем в МА-моделях — проблема долговременной устойчивости циклических колебаний. Наибольшую известность в этой связи получила модель Дж. Хикса. Экономику в целом,
по мнению Хикса, можно описать МА-моделью со взрывным акселератором (больше единицы). Но размер отклонений от равновесной
траектории сдерживается двумя ограничениями. Ограничение снизу вызвано тем, что валовые инвестиции всегда отрицательны и,
следовательно, при экзогенности автономного компонента спроса
весь доход не может опуститься ниже некоторой величины. Ограничение сверху — «потолок» — обуславливается наличными производственными ресурсами, что не позволяет сильно превысить равновесный уровень. Предполагается, что «потолок» лежит выше равновесной траектории и также может повышаться трендовыми темпами. Равновесие, описываемое МА-моделью, при взрывном акселераторе неустойчиво. Одиножды начавшись, колебания идут с увеличивающейся амплитудой до тех пор, пока в действие не вступают ограничения. В итоге решенными оказываются сразу две проблемы: цикл становится незатухающим, но размах колебаний имеет тенденцию оставаться постоянным.
Дж. Дьюзенберри, будучи противником «потолочных» теорий, предложил рассмотреть МА-модель со взрывным акселератором, но при этом обойтись только ограничениями снизу. Суть его идеи состоит в том, что для прекращения безудержного роста размаха колебаний достаточно одного нижнего ограничения. Таким образом, цикл по-прежнему остается незатухающим, а «потолок» оказывается ненужным.
К числу наиболее примечательных моделей неоклассического типа можно отнести модель X. Роуза и модель Р. Игли. Исходным пунктом анализа цикла здесь является рассмотрение условий предложения. Задается производственная функция, в соответствии с которой сочетание двух факторов — труда и капитала — определяет физический объем выпуска. Таким образом, в отличие от неокейнси-анцев, ставящих во главу угла движение платежеспособного спроса, неоклассики с самого начала сосредоточивают внимание на производстве и занятости.
Движение двух главных факторов производства описывается поведенческими функциями. Накопление капитала ставится в прямую зависимость от прибыли: чем больше прибыль, тем больше, при прочих равных условиях, величина чистых инвестиций. А величина занятости определяется исходя из имеющегося объема капитала.
Прибыль определяется по остаточному принципу как разность между общей величиной дохода (произведение цены на физический объем выпуска) и фондом заработной платы. Рассмотрение цен, даже если они введены в модель, остается вне рамок колебательного механизма как такового. Циклические изменения пропорции цены/издержки фактически выводятся из движения заработной платы. Подразумевается, что другие компоненты издержек не играют активной роли.
Основной акцент в неоклассических моделях сделан на объяснении динамики заработной платы. В основе способа описания ее движения лежит традиционная гипотеза о связи заработной платы с безработицей: чем выше занятость, тем при прочих равных условиях выше ставка заработной платы, и наоборот.
Перечисленных посылок достаточно, чтобы сконструировать простейший колебательный механизм. Попеременное расширение и сужение занятости порождает параллельные изменения в прибыльности и, соответственно, в темпах накопления капитала. Это, в свою очередь, обусловливает неравномерную динамику занятости. Таков основной контур причинно-следственных связей неоклассических моделей цикла.
Несмотря на различие описаний, оба механизма (неокейнсиан-цев и неоклассиков) оказываются на удивление похожими в целом ряде своих фундаментальных свойств. Различие между двумя концепциями происходит из-за неодинаковой интерпретации основных сил, приводящих в движение механизм колебаний, но структуры этого механизма оказываются во многом симметричными.
Обсуждение Моделирование экономических процессов
Комментарии, рецензии и отзывы
