8.3. модель бруно-фищера. смешанное финансирование дефицита государственного бюджета
8.3. модель бруно-фищера. смешанное финансирование дефицита государственного бюджета
Более сложная, но и более реалистичная версия модели, предполагает, что государство имеет возможность финансировать бюджетный дефицит не только при помощи денежной эмиссии, но и прибегая к заимствованиям. Бюджетный дефицит G Т
в модели финансируется либо за счет денежной эмиссии МІР,
либо за счет увеличения государственного долга В. Бюджетное ограничение государства записывается следующим образом:
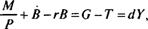
(8.20)
где В — величина реального государственного долга; г — реальная процентная ставка; d — доля бюджетного дефицита в ВВП.
Пусть V — богатство (сбережения) потребителей, складывающееся из двух активов: запаса государственных облигаций В и реального запаса наличных денег М/Р, V = В + М/Р; v = V/Y.
Тогда спрос экономических агентов на деньги может быть задан уравнением
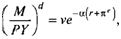
(8.21)
где г + ке = / — номинальная процентная ставка.
Выпишем условие равновесия на рынке товаров для случая, когда инвестиционный спрос является частью потребительного спроса:
Y = С + G. (8.22)
Предположим, что частное потребление С прямо пропорционально величине богатства К и обратно пропорционально ставке процента г. Кроме того, потребление снижается с ростом налогов Т.
С = ^--с{Г, у>0, с, >0. (8.23) г1
Тогда уравнение равновесия на рынке товаров будет выглядеть следующим образом [из (8.22) с учетом (8.23)]:
1 = Иг-т + (8.24)
у у у v '
Из (8.24) следует, что величина богатства (в долях ВВП) является возрастающей функцией от реального процента г и ставки налогов t = Т/Уи убывающей функцией от доли государственных расходов в ВВП £, = G/Y.
v = (l + c,/-$)r* = v(r, /), (8.25)
где у — параметр, характеризующий эластичность сбережений по ставке процента, у > 0.
Тогда бюджетное ограничение государства (8.20) может быть переписано как
Qz + o + nb = d + rb, (8.26)
где п — темп роста населения, совпадающего с темпом роста выпуска;
z — доля реальных денежных средств в ВВП; b = B/Y.
В состоянии равновесия Ь = 0, в = л + п, к' = п. Преобразовав (8.26), считая, что b = v — z (следует из определения v), получим
(n + r)z = d + (r-n)v. (8.27)
Наклон полученного бюджетного ограничения в координатах (я, г) равен
dr_ dn
z[-a{n + r)] b + aiz —L
(8.28)
Знак числителя (8.28) положителен при л<(1/а) — г и отрицателен при л >(1/а) — г. Знак знаменателя зависит от величины параметра у. Если значение эластичности сбережений по процентной ставке сравнительно мало (у < у*, где у* — значение параметра у, при котором знаменатель (8.28) обращается в ноль, у* = r(b + <xiz)/d), то знаменатель (8.28) положителен и верен рис. 8.4. Если значение у велико (у > у*), то знаменатель отрицателен и верен рис. 8.5.
і
--ч
GG,
GG
в*-п л* Г я
Рис. 8.4. Состояния равновесия в модели Бруно—Фишера при слабой чувствительности сбережений к изменениям процентной ставки (у < у*)
Рассмотрим три возможные стратегии государства в области финансирования бюджетного дефицита, используя рис. 8.4 и 8.5.
Пусть целью государства является поддержание реальной процентной ставки на постоянном уровне г*. Это означает, что правительство будет размещать на рынке такой объем государственных облигаций, чтобы реальная ставка процента сохранялась на уровне г*, а оставшийся бюджетный дефицит будет покрывать при помощи денежной эмиссии. Этому варианту кредитно-денежной политики на рис. 8.4 и 8.5 соответствует линия г = г*. При такой политике в экономике возможны два равновесных состояния А и В.
С другой стороны, государство может поддерживать постоянный темп роста денежной массы 0*, финансируя оставшийся
 |
дефицит при помощи государственных облигаций. Графически этот вариант кредитно-денежной политики можно представить линией тс = G* — п. В этом случае в экономике вне зависимости от значения эластичности сбережений по процентной ставке будет наблюдаться единственное равновесие С.
Наконец, Центральный банк может поддерживать постоянную номинальную ставку процента і*. В таком случае при низком у существует одно равновесие £"(рис. 8.4), а при высоких значениях у (рис. 8.5) возможно существование двух точек равновесия — Е и Z.
Какими будут последствия увеличения дефицита государственного бюджета в каждом из рассмотренных случаев? Ответ на этот вопрос зависит от того, какие из полученных равновесных состояний являются устойчивыми.
Увеличение бюджетного дефицита приведет к сдвигу кривой GG к GG, (вниз на рис. 8.4 и вверх на рис. 8.5). При относительно низком значении у увеличение бюджетного дефицита вызовет рост инфляции, если экономика находилась в равновесии А или Е, и падение инфляции, если экономика находилась в равновесии В.
Результатом увеличения бюджетного дефицита в случае у > у* будет увеличение темпов инфляции, если экономика находилась в равновесии А или Е, и снижение темпов инфляции, если экономика находилась в точке В или Z.
Исследуем полученные равновесные состояния модели на устойчивость. Предположим, что механизм формирования ожиданий тот же, что и в предыдущей модели
(8.13)
где (3 — скорость, с которой экономические агенты пересматривают свои инфляционные ожидания, Р > 0.
Перепишем бюджетное ограничение государства (8.27) как d + (r-n)b = Qz-v-i, (8.27') где z, напомним, задается уравнением (8.21).
Рассмотрим случай, когда целью государства является поддержание постоянного темпа роста денежной массы. Как уже было показано выше, в этом случае в экономике возможно единственное равновесное состояние. Из (8.13) и (8.27') с учетом (8.21) получим следующую систему дифференциальных уравнений, определяющую динамику модели вблизи точки равновесия:
(1-аР)+ а
rjyv
Р{Є-«-71Є +
уЛ г а-— — rjyv
[d + (r-n)v-z(r-nc)]
r/r = yv (1-сф) + (а-^)^
j {(l-ap)[rf + (r-n)v-sr]-Z{B-n-a$ne)}.
Можно показать, что если значение ар невелико и г > п, то при относительно низких значениях эластичности сбережений по ставке процента единственное равновесие в экономике не будет устойчивым (решение системы дифференциальных уравнений будет седловой точкой). Чем больше значение эластичности сбережений по ставке процента, тем вероятнее, что единственное равновесие окажется устойчивым.
Динамика системы в случае, когда государство поддерживает на постоянном уровне процентную ставку (реальную или номинальную), также определяется значениями параметров a, р и у.
В этом случае, как и в модели Бруно—Фишера, предполагающей эмиссионное финансирование бюджетного дефицита, в экономике возможно существование двух равновесных состояний, из которых низкоинфляционное будет устойчивым при оф < 1.
Иными словами, главный вывод модели Бруно—Фишера можно сформулировать следующим образом: при любом варианте финансирования бюджетного дефицита (как эмиссионном, так и смешанном) действенность антиинфляционных мер во многом зависит от того, как устроен механизм формирования инфляционных ожиданий в экономике. Возможна ситуация, когда традиционные, ортодоксальные меры борьбы с инфляцией, такие, как снижение бюджетного дефицита, стабилизация курса национальной валюты, укрепление независимости Центрального банка, сдерживание роста денежной массы и т. д., оказываются недостаточными. В этом случае предлагается использовать так называемые гетеродоксные меры, направленные на снижение инфляционных ожиданий экономических агентов (на модельном уровне это означает уменьшение значений параметров а и р), такие, как замораживание заработной платы и контроль цен.
Обсуждение Макроэкономика
Комментарии, рецензии и отзывы
