9.5. оценка темпов роста при переходе к устойчивому состоянию

9.5. оценка темпов роста при переходе к устойчивому состоянию

Выше было показано, что в устойчивом состоянии темпы роста не зависят от нормы сбережений и типа производственной функции. Проанализируем, от каких параметров зависят темпы роста капиталовооруженности и производительности труда1 при переходе от первоначального состояния к устойчивому.

Разделим обе части (9.5) на к, получим

| = ^-(» + g + 6). (9.12)

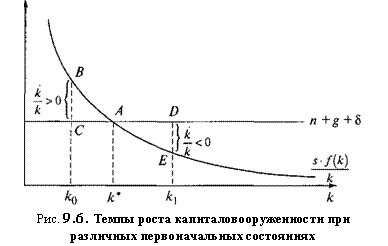
Формула (9.12) описывает темпы роста капиталовооруженности одного работника с постоянной эффективностью труда. На рис. 9.6 изображены темпы роста капиталовооруженности:

в устойчивом состоянии к* — это точка Л, так как темп роста равен 0;

для случая, когда первоначальное состояние ниже устойчивого уровня — отрезок ВС, темпы роста положительные;

для случая, когда первоначальное состояние выше устойчивого уровня — отрезок DE, темпы роста отрицательные.

вать следующим образом: V(*)'

Отрицательный наклон кривой і^йі можно проиллюстриро 

f(k)-kf'(k)

= v V s(9ЛЗ)

к К

Числитель правой части (9.13) представляет собой предельную производительность труда (в чем нетрудно убедиться, вспомнив,

что y = LEF-j-j;, 1 J) и поэтому больше 0. Следовательно,

'Здесь и далее под капиталовооруженностью и производительностью труда будем понимать эти показатели в расчете на единицу труда с постоянной эффективностью.

т. е. функция

убывающая.

Из рис. 9.6 видно, что при к0 < к* темпы роста капиталовооруженности положительны и убывают по мере приближения к устойчивому состоянию, а при к0 > к* — отрицательны и возрастают. Таким образом, при любом первоначальном уровне капиталовооруженности система приходит к устойчивому состоянию к*.

к к'

у_

У

Можно оценить также темпы роста производительности труда по мере перехода к устойчивому состоянию:

(9.14)

ff'(k)k

/(*)

Г{к)к

№

Темпы роста производительности труда равны произведению доли дохода на капитал в доходе и темпов роста капиталовооруженности.

С учетом (9.12) условие (9.14) можно переписать следующим образом:

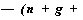
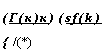
f'{k)k I /(*)

vа/ sf'(k)-(n + g + 5)

(9.15)

Выражение (9.15) позволяет найти зависимость темпов роста у от изменения капиталовооруженности к.

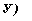
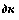= sf"{k)-{n + g + 5)

f"(k)kf(k) + f'{k)f{k) f'{k)kf'{k) fk)

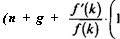f'(k)k^ /(*)

f"(k)k к , .

-jw-k-^^

f'(k)

1-

f'{k)k /(*) (9.16)

В правой части (9.16) выражение в квадратных скобках всегда положительно, так как доля дохода на капитал в доходе меньше 1. При к0<к* темп роста капиталовооруженности больше 0. f"{k) < 0 по свойству производственной функции. Следовательно, правая часть (9.16) отрицательна, т.е. темпы роста у падают с ростом к. При к0 > к* темпы роста капиталовооруженности меньше 0, поэтому правая часть (9.16) может быть как положительна, так и отрицательна, однако при приближении к устойчивому состоянию темпы роста капиталовооруженности стремятся к 0, поэтому правая часть (9.16), скорее всего, будет отрицательной и темпы роста Убудут падать. Динамика темпов роста потребления на одного работника с постоянной эффективностью труда повторяет динамику у, так как с составляет его постоянную часть (с = (1 — s)y).

Из проведенного анализа видно, что при прочих равных более низкий первоначальный уровень капиталовооруженности предполагает более высокие темпы экономического роста, которые затухают по мере приближения к устойчивому состоянию. Проанализируем, означает ли это, что со временем должно происходить сближение уровней жизни бедных и богатых стран, т. е. наблюдаться процессы конвергенции.