8.5. модель саржента-уоллеса
8.5. модель саржента-уоллеса
В модели [22, 24] предполагается, что государство имеет возможность финансировать бюджетный дефицит либо при помощи денежной эмиссии, либо за счет увеличения государственного долга. Правительство заранее планирует будущие значения бюджетных дефицитов, возможность финансирования которых за счет долга ограничена спросом на государственные облигации. Ставка процента превышает темп роста выпуска, поэтому в некоторый момент финансирование бюджетного дефицита становится возможным только за счет сеньоража. В результате темп роста денежной массы увеличивается, что приводит к повышению темпов инфляции.
Предпосылки модели:
ВВП (Y) и население (N) растет с постоянным темпом я:
Yt+x={+n)Y,; (8.29)
Nl+l={+n)Nr (8.30)
Модель Саржента—Уоллеса, как и предыдущие модели, предполагает, что денежная политика не способна повлиять на темп роста реального ВВП и на реальную процентную ставку.
Реальная процентная ставка г превышает темп роста экономики п:
г> п. (8.31)
Таким образом, долговое финансирование бюджетного дефицита рано или поздно должно привести к ситуации, когда государство не сможет погашать его за счет долга и будет вынуждено перейти к денежному финансированию. Это порождает в будущем усиление инфляционных процессов.
3. Эластичность спроса на деньги по доходу постоянна.
df Y
ч/г =^7"y=const<8-32)
Это означает, что скорость обращения денег остается постоянной.
Условия 1—3 представляют собой стандартные предпосылки, используемые во всех монетаристских моделях. В рамках этих предпосылок демонстрируется ограниченность возможностей контролировать инфляцию с помощью денежной политики.
Бюджетно-налоговая политика в модели задается последовательностью /),, D2, Dt, где D, — дефицит государственного бюджета в реальном выражении в момент времени t, т. е. государственные расходы (за исключением процентов но государственному долгу) минус налоговые поступления (за вычетом трансфертов). Кредитно-денежная политика представлена последовательностью Мх, М2, М,, где М, — денежная масса в момент времени Л
Модель показывает, что для любой заранее заданной последовательности Z)|, D2, Dp ... сдерживающая кредитно-денежная политика сегодня неизбежно приведет к росту уровня цен завтра. Более того, при определенных условиях долговое финансирование бюджетного дефицита и сдерживающая кредитно-денежная политика могут привести к росту цен не только в будущем, но и в настоящем.
Бюджетное ограничение государства в модели задается уравнением:
В, = М'~рМ'~1 +В,-В!_і{+г!_і), /=і,2,... (8.33)
где Р, — уровень цен в момент времени /;
В, — объем государственных облигаций в реальном выражении в момент времени t; rt_x — ставка доходности по государственным облигациям в момент времени /— 1.
Предполагается для простоты, что долг погашается в течение одного периода.
Разделив (8.33) на N, — численность населения в момент времени t и перегруппировав слагаемые, получим
В, _! + /-,_, D, М,-М,_х
N, 1+я А/,_, N, N,Pt ' ( '
Модель предполагает, что денежная масса растет с постоянным темпом 9 до момента Т, пока величина государственного долга на душу населения не достигает некого критического значения bT{Q). После этого величина долга на душу населения поддерживается па постоянном уровне, достигнутом к моменту Т.
М, = (1 + 9)Л/,_,, t= 2, Т. (8.35)
После момента Т государство вынуждено покрывать дефицит государственного бюджета только посредством денежной эмиссии, не наращивая более объем внутреннего долга.
Теперь можно проанализировать последствия выбора величины 0 и момента Т. Предположим, что последовательность
D2, D,, а также величины 6 и Т объявлены заранее в момент t = и известны экономическим агентам. Ожидания в модели носят рациональный характер, т. е. ожидаемый и фактический темпы инфляции совпадают.
Согласно предпосылкам скорость обращения денег и рост ВВП (равный темпу роста населения) постоянны. Из этих предположений в соответствии с уравнением количественной теории денег (которое в данном случае имеет вид M,V— P,Nty, где у — постоянный выпуск на душу населения) следует, что уровень цен в экономике в момент времени / пропорционален денежной массе.
(8.36)
Тогда из (8.36) с учетом (8.35) вытекает, что для периодов времени t = 2, Т P,/P,_i = (1 + 6)/(1 + п). Иными словами, задавая темп роста денежной массы 8 в период от 1 до Г при темпе экономического роста п, мы фактически выбираем темп инфляции для этого периода. Цель модели — проанализировать, как выбранный темп инфляции влияет на темпы инфляции в периодах, следующих за Т.
Подставив (8.36) в (8.34), считая, что для t> Твеличина долга на душу населения постоянна и составляет br(Q), получим следующее выражение:
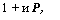
+ п
1 + г. |
МЄ) —
bT(Q) + dt-h
1
где
Отсюда
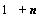
1
р,
d,+
'1-Х
1 + и
М9)
t>T.
(8.37)
По предположению (предпосылка 2) г,_, — п > 0. В условиях
инфляции < 1, поэтому левая часть (8.37) положительна. Тогда
из уравнения (8.37) следует, что чем выше bT(Q), тем больше левая
часть уравнения и, следовательно, ниже Р,_х/Pt, а значит, выше темпы инфляции Р,/Р,_х для всех t> Т.
Для того чтобы доказать, что сдерживающая кредитно-денежная политика приведет к росту уровня цен в будущем, осталось показать, что чем ниже темп прироста денежной массы 9, тем выше значение Ьт(в).
Решив (8.34) при /= 1 относительно bx(Q), получим
1 +п
1 +/п
4)
(8.38)
Заменим В0( + г0) в уравнении (8.38) на В0/Ри где В0 — приведенная к периоду 1 номинальная величина долга, выпущенного в период /=0. Эта подстановка позволяет избежать необходимости делать какие-либо предположения о виде зависимости между темпами инфляции в периодах 0 и 1, так как по условию темпы роста денежной массы 8 поддерживаются только начиная с периода 1.
л
(8.39)
Уравнение (8.39) с учетом (8.36) позволяет найти 6,(9) = b{
как зависимость от /),, Nx, М{, Л/0 и В0 (т. е. без использования темпа роста денежной массы между периодами 0 и 1).
Ц> + ф/,-л/0) 1 л/, 1 л/.
(8.39')
b2(Q)=^1bi+d2-h I + п
+ 9
Теперь, используя (8.34) и (8.36), найдем Л2(6), *з(9), Ьт(в).
ґ 0 ^
где и, описывается уравнением (8.39').
С учетом этого
Л, (9):
+п
b,_№) + d,-h
1 + 9
{ 9 ^
/=2,3,..., Т (8.40)
Подставляя 3 <t< Тв (8.40), получим
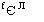
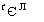
*3(Є):
+ d3-h
I + я
1 + я
ч1+е,
bx+d2-h
і+е)
(l+/j)(l+/-2) l + r2 1 + /2 ле AO
: — -г— о, -і а-) + а-і .
(1 + я)2 1 + я 1 + я 1 + в 1 + 9
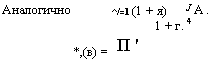 |
Г-1
+ 1
У =2 (1 + я)
'-7
И ' Д(1 + ,1)
J 1 + в А (! + /,)'->'
(8.41)
(-і
где
будем считать, что П(і + //) ~ 1, сели j = Л
Из уравнения (8.41) следует, что чем ниже 0, тем больше bj(Q). А это, в свою очередь, означает, что чем ниже 0, тем выше темп инфляции в период г > Т.
Итак, при предположении, что реальная ставка процента по государственному долгу в экономике превышает темпы экономического роста, было показано, что сдерживающая кредитно-денежная политика в настоящем приводит к высоким темпам инфляции в будущем.
В проведенном анализе спрос на деньги формировался в соответствии с количественной теорией денег (см. уравнение (8.34)). Кейнсианская функция спроса на деньги предполагает его зависимость не только от реального дохода, но и от номинальной ставки процента. Если доход и реальная ставка процента неизменны, то спрос на деньги меняется только при изменении инфляционных ожиданий. Эту зависимость можно выразить с помощью функции, аналогичной функции Кагана, тогда равновесие денежного рынка описывается уравнением
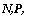 = а, -а,
= а, -а,
■/+1
(8.42)
где а,, а2 > 0.
р
Здесь -iii— ожидаемый темп инфляции, который при раци-Р/
ональных ожиданиях совпадает с фактическим; а, — автономный спрос на деньги; ос2 — чувствительность спроса на деньги к изменению инфляционных ожиданий.
Покажем, что при предположении (8.42) нынешние темпы инфляции зависят от ожидаемых в будущем темпов роста денежной массы. Уравнение (8.42) можно переписать в виде
1 М. ос, _
р,= ~л7^+ '+!■ (8-43)
a, N, а,
Аналогично можно выразить Р1+] и, подставив в (8.43), получить
р 1 М' , "2 Mt+ ,
' «і N, a, Nl+]
( V
Vа!
Р,+2-
С помощью подобных рекурсивных подстановок выразим текущий уровень цен в зависимости от ожидаемых в будущем темпов роста денежной массы
( V
°-l j = 0
+j
ТГ(8-44)
Таким образом, темп инфляции сегодня зависит не только от текущей, но и от ожидаемой в будущем денежной политики. Если в настоящий момент проводится ограничительная денежная политика, но в будущем ожидается повышение темпа роста денежной массы, то это может привести к инфляции уже в текущем периоде. Из (8.44) видно, что вероятность такого исхода тем выше, чем больше ос2, т. е. чувствительность спроса на деньги к изменению ожидаемых темпов инфляции.
Модель Саржента—Уоллеса демонстрирует, что при сделанных предпосылках ограничительная кредитно-денежная политика в настоящем приводит к инфляции в будущем, а при неблагоприятных условиях может вызвать инфляцию уже в текущем периоде. Более того, Саржент и Уоллес построили числовые примеры, показывающие, что возможны: 1) случаи, когда сдерживающая кредитно-денежная политика в настоящем приводит в будущем к более высоким темпам инфляции, чем они были бы при менее жесткой политике; 2) случаи, когда сдерживающая кредитно-денежная политика уже в текущем периоде приводит к более высоким темпам инфляции, чем они были бы при менее ограничительной политике. Причем вероятность такого исхода зависит от нервозности поведения экономических агентов. Этот вывод перекликается с результатами модели Бруно—Фишера. Следует отметить, что ограниченность возможностей применения денежной политики для борьбы с инфляцией продемонстрирована в рамках стандартных монетаристских предпосылок.
Модель Саржента—Уоллеса сравнивает последствия денежного и долгового финансирования дефицита государственного бюджета. Если экономические агенты ожидают, что правительство вынуждено будет в будущем в некоторый момент времени Т перейти от долгового финансирования бюджетного дефицита к денежному, то они считают, что низкий рост денежной массы означает более быстрый рост долга. Следовательно, после Г правительство будет быстро наращивать денежную массу. Ожидание столь быстрого роста предложения денег в будущем вызовет быстрый рост инфляции в настоящем. Саржент и Уоллес показали, что инфляция в этом случае может расти в ответ на снижение темпов роста денежной массы, т. е. инфляция в случае долгового финансирования может оказаться выше, чем при денежном. С этой точки зрения единственно надежным средством борьбы с инфляцией является достижение профицита государственного бюджета.
Все рассмотренные в этой главе модели демонстрируют ограниченность в ряде случаев возможностей применения стандартных монетаристских рекомендаций для борьбы с инфляцией. Последствия ограничительной кредитно-денежной политики, как было показано, существенным образом зависят от характера поведения экономических агентов. Это обстоятельство необходимо учитывать при проведении экономической политики.
1. В странах Си/) наблюдаются высокие темпы инфляции. В стране С спрос на реальные запасы денежных средств описыва-
ется функцией Кагана вида:
уР J
= е
-0.7пс
В стране D спрос на
= е
реальные запасы денежных средств также описывается функцией
,-0,1 ж'
Кагана вида:
В странах С и D инфляционные ожидания экономических агентов носят адаптивный характер, причем инфляционные ожидания в них изменяются на 2 п. п., если фактический темп инфляции отклоняется от ожидаемого на 1 п. п.
Центральные банки этих стран поддерживают постоянный темп роста денежной массы в 3\%.
Используя модель Кагана, ответьте на следующие вопросы.
а) Придут ли денежные рынки этих стран в равновесие? При
каких темпах инфляции оно будет достигнуто?
б) Если нет, то какие меры требуются для достижения равновесия?
Объясните свой ответ.
:е-ож
Пусть в странах А и В бюджетный дефицит покрывается целиком за счет эмиссии. Доля бюджетного дефицита в выпуске постоянна и составляет 5\%. Выпуск растет с постоянным темпом в 3\%. Спрос на реальные запасы денежных средств (в долях ВВП)
(М v
в этих странах описывается функцией Кагана -г—
\"'
В странах А и В инфляционные ожидания экономических агентов носят адаптивный характер:
в стране А инфляционные ожидания изменяются на 3 п. п., если фактический темп инфляции отклоняется от ожидаемого на 1 п. п.;
в стране В инфляционные ожидания изменяются на 1,5 п. п., если фактический темп инфляции отклоняется от ожидаемого на 1 п. п.
Следует ли в этих странах для борьбы с инфляцией использовать такую меру, как снижение бюджетного дефицита? Если нет, то почему и какие меры следует предпринять. Поясните свой ответ, используя модель Бруно—Фишера.
Пусть в модели Бруно—Фишера (случай эмиссионного финансирования бюджетного дефицита) соотношение доли бюджетного дефицита в выпуске и темпов роста ВВП таково, что имеет место единственное равновесие в точке касания линий пе = deaK — р и тс= ке (см. рис. 8.1).
Определите темп инфляции, при котором достигается это равновесие.
Является ли оно устойчивым? Как изменятся темпы инфляции в случае снижения бюджетного дефицита? Зависит ли ответ от характера поведения экономических агентов?
Изобразите равновесие в модели Бруно—Фишера (случай эмиссионного финансирования бюджетного дефицита) в координатах: темп роста денежной массы (9) — ожидаемый темп инфляции (ле). Проведите анализ устойчивости стационарных состояний в этих координатах. Исследуйте последствия снижения бюджетного дефицита с помощью полученного графика.
Одной из ключевых предпосылок модели Саржента— Уоллеса является превышение реальной ставкой процента темпа роста выпуска. Предположим, что темпы роста выпуска превышают реальную ставку процента. Останутся ли в силе выводы модели? Объясните свой ответ.
Как изменятся выводы модели Саржента—Уоллеса, если в каждом периоде ставки процента окажутся выше, чем предполагалось первоначально? Объясните свой ответ.
Обсуждение Макроэкономика
Комментарии, рецензии и отзывы
