Приложение а
Приложение а

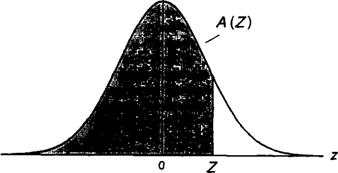
Л (Z) — это интеграл функции плотности вероятности стандартизированного нормального распределения от — ©о до Z (другими словами, площадь под кривой слева от Z). A (Z) дает вероятность того, что величина нормально распределенной случайной переменной не превысит среднее значение больше, чем на Z стандартных отклонений.
Значения Z, играющие важную роль в книге:
Z A(Z)
1,645 0,950 нижняя граница правой 5-процентной области 1,960 0,975 нижняя граница правой 2,5-процентной области 2,326 0,990 нижняя граница правой однопроцентной области 2,576 0,995 нижняя граница правой 0,5-процентной области
0,00
0,01 0,02
0,03
A(Z) 0,04 0,05
0,06
0,07 0,08
0,09
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0
0,5000 0,5398 0,5793 0,6179 0,6554 0,6915 0,7257 0,7580 0,7881 0,8159 0,8413 0,8643 0,8849 0,9032 0,9192 0,9332 0,9452 0,9554 0,9641 0,9713 0,9772 0,9821 0,9861 0,9893 0,9918 0,9938 0,9953 0,9965 0,9974 0,9981 0,9987 0,5040 0,5438 0,5832 0,6217 0,6591 0,6950 0,7291 0,7611 0,7910 0,8186 0,8438 0,8665 0,8869 0,9049 0,9207 0,9345 0,9463 0,9564 0,9649 0,9719 0,9778 0,9826 0,9864 0,9896 0,9920 0,9940 0,9955 0,9966 0,9975 0,9982 0,5080 0,5478 0,5871 0,6255 0,6628 0,6985 0,7324 0,7642 0,7939 0,8212 0,8461 0,8686 0,8888 0,9066 0,9222 0,9357 0,9474 0,9573 0,9656 0,9726 0,9783 0,9830 0,9868 0,9898 0,9922 0,9941 0,9956 0,9967 0,9976 0,9982 0,5120 0,5517 0,5910 0,6293 0,6664 0,7019 0,7357 0,7673 0,7967 0,8238 0,8485 0,8708 0,8907 0,9082 0,9236 0,9370 0,9484 0,9582 0,9664 0,9732 0,9788 0,9834 0,9871 0,9901 0,9925 0,9943 0,9957 0,9968 0,9977 0,9983 0,5160 0,5557 0,5948 0,6331 0,6700 0,7054 0,7389 0,7704 0,7995 0,8264 0,8508 0,8729 0,8925 0,9099 0,9251 0,9382 0,9495 0,9591 0,9671 0,9738 0,9793 0,9838 0,9875 0,9904 0,9927 0,9945 0,9959 0,9969 0,9977 0,9984 0,5199 0,5596 0,5987 0,6368 0,6736 0,7088 0,7422 0,7734 0,8023 0,8289 0,8531 0,8749 0,8944 0,9115 0,9265 0,9394 0,9505 0,9599 0,9678 0,9744 0,9798 0,9842 0,9878 0,9906 0,9929 0,9946 0,9960 0,9970 0,9978 0,9984 0,5239 0,5636 0,6026 0,6406 0,6772 0,7123 0,7454 0,7764 0,8051 0,8315 0,8554 0,8770 0,8962 0,9131 0,9279 0,9406 0,9515 0,9608 0,9686 0,9750 0,9803 0,9846 0,9881 0,9909 0,9931 0,9948 0,9961 0,9971 0,9979 0,9985 0,5279 0,5675 0,6064 0,6443 0,6808 0,7157 0,7486 0,7794 0,8078 0,8340 0,8577 0,8790 0,8980 0,9147 0,9292 0,9418 0,9525 0,9616 0,9693 0,9756 0,9808 0,9850 0,9884 0,9911 0,9932 0,9949 0,9962 0,9972 0,9979 0,9985 0,5319 0,5714 0,6103 0,6480 0,6844 0,7190 0,7517 0,7823 0,8106 0,8365 0,8599 0,8810 0,8997 0,9162 0,9306 0,9429 0,9535 0,9625 0,9700 0,9761 0,9812 0,9854 0,9887 0,9913 0,9934 0,9951 0,9963 0,9973 0,9980 0,9986 0,5359 0,5753 0,6141 0,6517 0,6879 0,7224 0,7549 0,7852 0,8133 0,8389 0,8621 0,8830 0,9015 0,9177 0,9319 0,9441 0,9545 0,9633 0,9706 0,9767 0,9817 0,9857 0,9890 0,9916 0,9936 0,9952 0,9964 0,9974 0,9981 0,9986
Источник: Pearson E.S., Harley H.O. (editors), Biometrika Tables for Statisticians, Cambridge, Cambridge University Press, 1970 (перепечатано с любезного разрешения Biometrika Trustees).
{-распределение: критические значения t
| Число | Тесты | Уровень значимости | |||||
| степеней | Двусторонний | 10\% | 5\% | 2\% | 1\% | 0,2\% | 0,1\% |
| свободы | Односторонний | 5\% | 2,5\% | 1\% | 0,5\% | 0,1\% | 0,05\% |
| 1 | 6,314 | 12,706 | 31,821 | 63,657 | 318,31 | 636,62 | |
| 2 | 2,920 | 4,303 | 6,965 | 9,925 | 22,327 | 31,598 | |
| 3 | 2,353 | 3,182 | 4,541 | 5,841 | 10,214 | 12,924 | |
| 4 | 2,132 | 2,776 | 3,747 | 4,604 | 7,173 | 8,610 | |
| 5 | 2,015 | 2,571 | 3,365 | 4,032 | 5,893 | 6,869 | |
| 6 | 1,943 | 2,447 | 3,143 | 3,707 | 5,208 | 5,959 | |
| 7 | 1,895 | 2,365 | 2,998 | 3,499 | 4,785 | 5,408 | |
| 8 | 1,860 | 2,306 | 2,896 | 3,355 | 4,501 | 5,041 | |
| 9 | 1,833 | 2,262 | 2,821 | 3,250 | 4,297 | 4,781 | |
| 10 | 1,812 | 2,228 | 2,764 | 3,169 | 4,144 | 4,587 | |
| 11 | 1,796 | 2,201 | 2,718 | 3,106 | 4,025 | 4,437 | |
| 12 | 1,782 | 2,179 | 2,681 | 3,055 | 3,930 | 4,318 | |
| 13 | 1,771 | 2,160 | 2,650 | 3,012 | 3,852 | 4,221 | |
| 14 | 1,761 | 2,145 | 2,624 | 2,977 | 3,787 | 4,140 | |
| 15 | 1,753 | 2,131 | 2,602 | 2,947 | 3,733 | 4,073 | |
| 16 | 1,746 | 2,120 | 2,583 | 2,921 | 3,686 | 4,015 | |
| 17 | 1,740 | 2,110 | 2,567 | 2,898 | 3,646 | 3,965 | |
| 18 | 1,734 | 2,101 | 2,552 | 2,878 | 3,610 | 3,922 | |
| 19 | 1,729 | 2,093 | 2,539 | 2,861 | 3,579 | 3,883 | |
| 20 | 1,725 | 2,086 | 2,528 | 2,845 | 3,552 | 3,850 | |
| 21 | 1,721 | 2,080 | 2,518 | 2,831 | 3,527 | 3,819 | |
| 22 | 1,717 | 2,074 | 2,508 | 2,819 | 3,505 | 3,792 | |
| 23 | 1,714 | 2,069 | 2,500 | 2,807 | 3,485 | 3,767 | |
| 24 | 1,711 | 2,064 | 2,492 | 2,797 | 3,467 | 3,745 | |
| 25 | 1,708 | 2,060 | 2,485 | 2,787 | 3,450 | 3,725 | |
| 26 | 1,706 | 2,056 | 2,479 | 2,779 | 3,435 | 3.707 | |
| 27 | 1,703 | 2,052 | 2,473 | 2,771 | 3,421 | 3,690 | |
| 28 | 1,701 | 2,048 | 2,467 | 2,763 | 3,408 | 3,674 | |
| 29 | 1,699 | 2,045 | 2,462 | 2,756 | 3,396 | 3,659 | |
| 30 | 1,697 | 2,042 | 2,457 | 2,750 | 3,385 | 3,646 | |
| 40 | 1,684 | 2,021 | 2,423 | 2,704 | 3,307 | 3,551 | |
| 60 | 1,671 | 2,000 | 2,390 | 2,660 | 3,232 | 3,460 | |
| 120 | 1,658 | 1,980 | 2,358 | 2,617 | 3,160 | 3,373 | |
| оо | 1,645 | 1,960 | 2,326 | 2,576 | 3,090 | 3,291 | |
Источник: Pearson E.S., Harley И.О. (editors), Biometrika Tables for Statisticians, Cambridge, Cambridge University Press, 1970 (перепечатано с любезного разрешения Biometrika Trustees).
Пример. Для распределения с 25 степенями свободы вероятность того, что t будет больше 2,060, равна 0,025 и вероятность того, что t будет меньше 2,060, составит 0,025. Если гипотеза отвергается в обеих крайних областях, т. е. в двустороннем тесте, то уровень значимости равен 0,05 (5\%). Если гипотеза отвергается в одной крайней области, т. е. при одностороннем тесте, то уровень значимости составит 0,025 (2,5\%). Более подробные разъяснения см. в главе 3.
F-распределение: критические значения f су, и у, степенями свободы, уровень значимости в 5\%
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | в | 9 | 10 | 12 | 15 | 20 | 24 | 30 | 40 | 60 | 120 | ||
| 1 | 161,4 | 199.5 | 215,7 | 224,6 | 230.2 | 234,0 | 236,8 | 238,9 | 240,5 | 241.9 | 243,9 | 245.9 | 248.0 | 249,1 | 250,1 | 251.1 | 252.2 | 253.3 | 254,3 |
| 2 | 18.51 | 19,00 | 19,16 | 19,25 | 19,30 | 19.33 | 19,35 | 19.37 | 19.38 | 19,40 | 19,41 | 19.43 | 19,45 | 19,45 | 19.46 | 19.47 | 19.48 | 19.49 | 19,50 |
| 3 | 10,13 | 9.55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,89 | 8.85 | 8,81 | 8,79 | 8.74 | 8.70 | 8.66 | 8,64 | 8.62 | 8,59 | 8,57 | 8.55 | 8,53 |
| 4 | 7.71 | 6,94 | 6.59 | 6.39 | 6,26 | 6.16 | 6.09 | 6.04 | 6.00 | 5.96 | 5,91 | 5,86 | 5,80 | 5.77 | 5.75 | 5.72 | 5.69 | 5.66 | 5.63 |
| 5 | 6,61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | 4.88 | 4,82 | 4.77 | 4.74 | 4,68 | 4.62 | 4.56 | 4,53 | 4.50 | 4.46 |
Обсуждение Введение в эконометрикуКомментарии, рецензии и отзывы Приложение а: Введение в эконометрику, Кристофер Доугерти, 1999 читать онлайн, скачать pdf, djvu, fb2 скачать на телефон Книга Кристофера Доугерти — один из самых популярных на Западе вводных учебников эконометрики для студентов-экономистов. Курс эконометрики занимает важное место в современных программах экономических вузов во всем мире наряду с такими предметами...
|
