10.5. гипотеза фридмена о постоянном доходе
10.5. гипотеза фридмена о постоянном доходе
Хотя первым модель адаптивных ожиданий предложил Ф. Кейган, самым известным ее приложением, без сомнения, является модель потребления, основанная на гипотезе Фридмена о постоянном доходе (Friedman, 1957). Как было показано в разделе 8.3, в этой модели постоянное потребление индивида / в период /, обозначаемое Cpjn предполагается пропорциональным его постоянному доходу Ypit
С£ =ptf. (10.39) Далее предполагается, что фактический объем потребления Сп и фактический уровень дохода Yit включают временные составляющие CTitw YTjt соответственно, которые зависят от ситуации в году £
СИ=С£ + СТ; (10.40)
*W/ + r/ (10.41)
Предполагается, что временная составляющая потребления и временная составляющая дохода являются случайными переменными со средним значением 0 и постоянными значениями дисперсии, распределенными независимо от величины постоянного дохода, постоянного потребления и друг от друга.
Величина постоянного дохода в уравнении (10.39) ненаблюдаема. Для решения этой проблемы М. Фридмен расширил свою модель, предположив, что изменение постоянного дохода подчиняется процессу адаптивных ожиданий. Если фактический текущий доход индивида выше (или ниже) величины его постоянного дохода в предыдущем периоде, то индивид увеличивает (или уменьшает) значение последнего путем умножения x на соответствующую разность:
AY,f =\<ylt-Yg_x). (10.42)
В общем случае предполагается, что величина x лежит в границах между 0 и 1. Индивиды корректируют свое представление о постоянном доходе с ростом фактического дохода, но не на полное значение прироста, сознавая, что изменения фактического дохода частично объясняются вариацией временной составляющей дохода.
Выражение (10.42) может быть переписано как
rif-YgLx-UYn-Y^). (Ю-43)
или
Y? =Ylt + (-)Y£l. (10.44)
Это уравнение имеет простую интерпретацию. Оно говорит, что оценка индивидом величины постоянного дохода в году t равна средневзвешенной величине текущего фактического дохода и предыдущей оценки постоянного дохода. Если величина x близка к единице, то индивид придает больший вес фактическому доходу, и значение Yp быстро приближается к Y. Если величина А,, наоборот, близка к нулю, то фактическому доходу придается относительно меньший вес и процесс корректировки происходит медленно.
Подставив величину Cpit из формулы (10.40) в (10.39), мы имеем:
C^-C^ptf, (10.45)
или
C,.,=pr,.f +CJ. (10.46)
В итоге мы получили соотношение между фактическим потреблением и постоянным доходом, где CTit играет роль случайного члена, который до этого отсутствовал в модели.
Использование фактического текущего значения дохода в качестве «заменителя» для показателя постоянного дохода в случае принятия гипотезы о постоянном доходе неприемлемо, поскольку это дает, как было показано в разделе 8.3, смещенные и несостоятельные оценки параметров. Вместо этого М. Фрид-мен использовал уравнение (10.44) для оценки связи постоянного дохода с текущим и прошлыми фактическими значениями дохода. Конечно, уравнение (10.44) не может использоваться напрямую для измерения постоянного дохода в году / по двум причинам: мы не знаем значения X и нет метода измерения Y?j_v Вторую причину можно устранить, заметив, что если выражение (10.44) выполняется для периода /, то оно выполняется также и для периода (/— 1):
ї£і=^,-і+(1-Щ£2(10.47) Подставив это выражение в (10.44), мы получим:
Ys* = XYit + X(l X)Yit.{ + (1 X)2Y,l2. (10.48)
Конечно, это уравнение включает ненаблюдаемую составляющую Ypjr_2, но можно устранить ее, сдвинув выражение (10.44) на два периода назад и подставив его в (10.48), получить таким образом зависимость Yp от Yin Yit_{9 Yit_2 и Ypit_y Повторяя эту процедуру до бесконечности, можно выразить Ypit как взвешенную сумму текущего и прошлых фактических значений дохода:
Yff = XYit + X(l Х)У/М + Х(1 Х)2У„_2 + Х(1 Х)3У„_3 + .... (10.49)
Опираясь на обоснованное предположение о том, что значение X лежит в границах от 0 до 1, можно сделать вывод, что (1 — X) лежит в тех же границах, а следовательно, величина (1 — X)s убывает с ростом s. Это свидетельствует о том, что текущее значение дохода имеет самый большой вес, значение дохода в предыдущем периоде имеет более низкий вес и значение этого веса постепенно убывает по мере продвижения назад к более отдаленным прошлым периодам. В конце концов оно становится настолько малым, что все предшествующие значения можно не принимать во внимание.
Тем не менее остается проблема оценки величины X. Решение М. Фридмена схоже с решением, предложенным Ф. Кейганом в его исследовании гиперинфляции. Он испытал большое число различных значений X между 0 и 1, рассчитал соответствующие ряды постоянного дохода для каждого из них, построил уравнения зависимости потребления для каждого ряда данных о постоянном доходе, используя коэффициент R2 для измерения качества оценки. Затем он выбрал то значение X, которое позволяло получить ряд Yp, дающий наилучшую оценку.
Динамические свойства модели
Динамические свойства модели Фридмена удобнее анализировать после проведения преобразования Койка. Предположим, что мы используем агрегированные данные, и поэтому индекс / можно опустить. Подставив выражение (10.44) в (10.46), мы получим:
с, = pxr,+Р(1-Х)Г£ + С/
(10.50)
Сдвигая выражение (10.45) на один период назад, имеем:
РГД =С/.1-С/7:1. (10.51)
Подставив это выражение в (10.50), получим:
С, = рХ Yt + (1 )Ct_x +Cj (1 Х)С^!. (10.52)
Это уравнение позволяет одновременно оценить краткои долгосрочную предельную склонность к потреблению. Краткосрочная предельная склонность к потреблению ЭС,/ЭУ, равна коэффициенту при Yn то есть РА,. Слагаемое (1 — А)СМ в краткосрочном аспекте выступает как константа, поскольку изменение Yt не может сказываться на значении См.
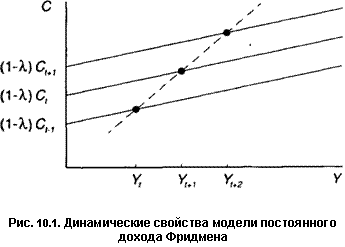 |
Зависимость для состояния долгосрочного равновесия, без учета случайного члена, может быть получена подстановкой С, = Ct_{ = С и У, = Y в формулу (10.52):
С = РХГ + (1-Х)С, (10.53) что может быть упрощено до вида:
c = pr.
(10.54)
Модель сводится к фридменовской зависимости постоянного потребления от дохода с равным нулю свободным членом и коэффициентом наклона, равным р. Угол наклона краткосрочной функции рА, оказывается меньше, поскольку значение X находится в границах между 0 и 1. Следовательно, модель Фридмена объясняет сосуществование краткосрочной предельной склонности к потреблению, меньшей единицы, и приблизительно постоянной средней склонности к потреблению, которое в послевоенные годы было загадкой для эконометри-стов. Заметим, однако, что модель Брауна, представленная в упражнении 10.7, приводит к похожему уравнению. Здесь мы имеем пример двух радикально различных экономических моделей, приводящих к одинаковой зависимости между наблюдаемыми переменными. Верно также, что если случайный член в поведенческом уравнении удовлетворяет условиям Гаусса—Маркова, то он будет также удовлетворять им в преобразованной по Койку модели Брауна, но не в модели Фридмена, где он будет отрицательно коррелировать со своим значением в следующий период, и поэтому МНК окажется неприменимым. В принципе этот вывод может быть положен в основу для выбора модели, но если есть причины полагать, что случайный член в поведенческом уравнении может не удовлетворять требуемым условиям, то данный мотив для выбора модели становится неприемлемым.
Пример
Для сравнения своего варианта функции потребления с другими функциями М. Фридмен оценил ее на годовых рядах данных о реальном потреблении на душу населения и о реальном располагаемом доходе на душу населения в США в период 1905—1951 гг., за исключением военных лет (Friedman, 1957, pp. 142— 152). В пошаговом поиске он рассчитал значения постоянного дохода как взвешенную сумму текущего и 16 предшествующих значений дохода, и оптимальное значение X оказалось равным 0,37. В уравнении функции потребления он получил значение р = 0,88. Как следствие, краткосрочная предельная склонность к потреблению была равна 0,33, а краткосрочный мультипликатор — 1,5. Долгосрочные показатели составили 0,88 и 8,5 соответственно.
Упражнение
10.10. Исследователь полагает, что расходы на одежду определяются следующей моделью:
log у, = а + p,log zt + P2log/>, + u, (I)
где уj — расходы на одежду (млрд. долл., в постоянных ценах); zr — постоянный доход; р} — реальный индекс цен на одежду (отнесенный к уровню инфляции). Исследователь также полагает, что постоянный доход зависит от фактического дохода хг согласно следующему уравнению:
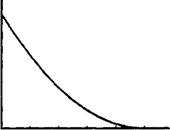
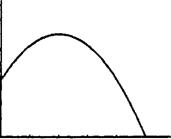
щих и лаговых значений х, то веса в этой зависимости подчиняются полиномиальному распределению. По этой причине лаги Алмон также часто описываются как полиномиально распределенные лаги. Приведем простые примеры, когда значения весов подчиняются квадратичной зависимости (как на рис. 10.2А и 10.2Б) кубической функции (как на рис. 10.3) или полиному более высокой степени. Выбор функции остается за исследователем, и он, конечно, может быть сделан на основе экспериментов.
Вес лагов Вес лагов
 А Б
А Б
f М f-2 f-3 f-4 f-5
f M f-2 f-3 f-4 f-5
Рис. 10.2
В общем случае модель регрессии может быть записана как
у, = а + рл + рЛ-, + + РЛ-* + ип (Ю.55)
где
Р, = Ъ + V + Ъ*1 + + У^- (10-56)
Рисунки 10.2А и 10.2Б, следовательно, соответствуют случаю, когда величина т =2, рис. 10.3 — случаю, когда т =3.
 Далее исследователь должен выбрать число лаговых значений объясняющей переменной п, которое будет использоваться в модели. И снова это число может быть определено в результате экспериментов, направленных на получение хорошего описания имеющихся данных.
Далее исследователь должен выбрать число лаговых значений объясняющей переменной п, которое будет использоваться в модели. И снова это число может быть определено в результате экспериментов, направленных на получение хорошего описания имеющихся данных.
t М f-2 f-3 f-4 f-5
Вес лагов
у, = а + РоХ, + р,*,., + Р2х,_2 + Р3х,_з + и, = = а + уЛ + (у0 + у, + у2) х, _ 1 + (у0 42у, + 4у2) х^2 + (у0 + Зу, + 9у2) х,_3 + и, = = а + у0(х, + x^j + х,_2 + х,_3) + УіСх^і + 2x^2 + 3х^.3) + y2(xt_{ + 4х^2 + 9х,_3) + и = = « + Yo*o + у,*, + Y2*2 + (10.57)
ГДЄ ^ = *,+ Vl + *л-2 + *>-3> *1 = *М + 2хл-2 + 3*л-3 И *2 = Xr~ + 4*r-2 + 9хг-3'
Для оценки параметров модели следует построить уравнение зависимости у не от текущего и лаговых значений х, а от сконструированных из них переменных Большинство статистических программ позволяют легко сделать это. С их помощью можно получить коэффициенты при сконструированных переменных, а на их основе — рассчитать коэффициенты в исходной модели.
Как видно из рис. 10.2А, сначала возрастающее, а затем убывающее распределение лагов в принципе может быть представлено квадратичной функцией. Однако у этого распределения имеется нежелательное свойство: выпуклый вверх график функции не позволяет весам плавно приближаться к нулю. С этой точки зрения кубическая функция на рис. 10.3, у которой две экстремальные точки, более привлекательна: в окрестности второй экстремальной точки происходит плавное убывание весов.
На практике распределение лагов объясняющей переменной может не соответствовать простой функции, и попытки их применения могут привести к нежелательным результатам: получение весов с неверными знаками, резкое уменьшение весов на краю распределения и т. д. Все эти проблемы в принципе можно преодолеть, используя полиномы более высокой степени: сама Ш. Ал-мон в своей статье использовала полином четвертой степени, получив вполне удовлетворительные результаты. Однако с ростом степени полиномов вновь возникает риск появления неучтенной мультиколлинеарности. Число переменных z равно числу слагаемых в полиноме, и переменные z коррелируют друг с другом, поскольку каждая из них является линейной комбинацией текущего и лаговых значений х.
Остается большой соблазн испытать все кажущиеся возможными комбинации степени полинома и числа лаговых значений и выбрать ту из них, которая дает результаты, наиболее близкие к априорным представлениям или по крайней мере наименее противоречащие им. В итоге вместо того, чтобы служить независимым тестом для гипотез,'эксперимент превращается в поиск подтверждений для априорных представлений.
Пример
При построении уравнения регрессионной зависимости расходов на жилье от личных доходов и реального индекса цен на жилье по данным за период 1959— 1983 гг. из табл. 6.9 было решено использовать описанную выше схему Алмон (квадратичная функция, три лаговых периода) для переменных дохода и цен. В уравнении регрессии, совпадающем с (10.57), постоянный член оказался равен —2,33, коэффициенты при Zq, z{ и z2 Для переменной дохода были равны 0,417, -0,159 и 0,025 соответственно, откуда следовало, что полиномиальная функция имела вид:
р, = 0,417 0,159* + 0,025*2. (10.58)
Подставляя в этой формуле для s значения 0, 1, 2 и 3, можно получить коэффициенты при текущем и лаговых значениях х:
I6g у{ = -2,33 + 0,417 log х, + 0,283 log хм + 0,199 log х^2 +
+ 0,165 log Xf_2 + Слагаемые для цен. (10.59)
В данном случае график квадратичной функции оказался вогнутым вниз, как на рис. 10.2Б, и распределение лагов имеет такой же вид, как и укороченное распределение Койка.
Упражнение
10.11. Коэффициенты при Zq, zx и z2 для переменной цен в регрессионном уравнении расходов на жилье были равны —0,035, 0,249 и —0,165, соответственно. Рассчитайте коэффициенты при log pn log />,_,, log Pf_2 и log р^ъ и прокомментируйте полученный результат.
Обсуждение Введение в эконометрику
Комментарии, рецензии и отзывы
