7.2. гетероскедастичность и ее последствия
7.2. гетероскедастичность и ее последствия
Во втором условии Гаусса—Маркова утверждается, что дисперсия случайного члена в каждом наблюдении должна быть постоянной. Такое утверждение может показаться странным, и здесь требуется пояснение. Случайный член в каждом наблюдении имеет только одно значение, и может возникнуть вопрос о том, что означает его «дисперсия».
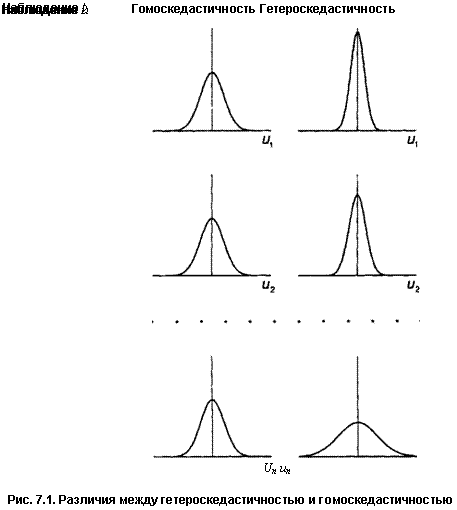
Имеется в виду его возможное поведение до того, как сделана выборка. Когда мы записываем модель (7.1), первые два условия Гаусса—Маркова указывают, что случайные члены и2, ипв п наблюдениях появляются на основе вероятностных распределений, имеющих нулевое математическое ожидание и одну и ту же дисперсию. Их фактические значения в выборке иногда будут положительными, иногда — отрицательными, иногда — относительно далекими от нуля, иногда — относительно близкими к нулю, но у нас нет причин a priori ожидать появления особенно больших отклонений в любом данном наблюдении. Другими словами, вероятность того, что величина и примет какое-то данное положительное (или отрицательное) значение, будет одинаковой для всех наблюдений. Это условие известно как гомоскедастичность, что означает «одинаковый разброс». Оно проиллюстрировано в левой части рис. 7.1.
Вместе с тем для некоторых выборок, возможно, более целесообразно предположить, что теоретическое распределение случайного члена является разным для различных наблюдений в выборке. В правой части рис. 7.1 дисперсия величины ui увеличивается по мере продолжения выборочных наблюдений. Это не означает, что случайный член обязательно будет иметь особенно большие (положительные или отрицательные) значения в конце выборки, но это значит, что априорная вероятность получения сильно отклоненных величин будет относительно высока. Это пример гетероскедастичность что означает «неодинаковый разброс». Математически гомоскедастичность и гетероскедастичность могут определяться следующим образом:
Гомоскедастичность: pop. var (uj) = а2 постоянна для всех наблюдений;
Гетероскедастичность: pop. var (ut) = а,.2, она не обязательно одинакова для всех /.
На рис. 7.2 показано, как будет выглядеть характерная диаграмма рассеяния, если у — возрастающая функция от х и имеется гетероскедастичность типа, показанного на рис. 7.1. Можно видеть, что, хотя наблюдения не обязательно все дальше отстоят от основной нестохастической составляющей линии регрессии у = а + рх, по мере роста х все же имеется тенденция к увеличению их
 |
разброса. (Следует иметь в виду, что гетероскедастичность не обязательно относится к типу, показанному на рис. 7.1. Данное понятие относится к любому случаю, в котором дисперсия вероятностного распределения случайного члена различна для разных наблюдений.)
Возникает вопрос, почему гетероскедастичность имеет существенное значение. В самом деле, соответствующее условие Гаусса—Маркова пока не использовалось в проводимом анализе, и оно может показаться практически не нужным. В частности, при рассмотрении простой модели (7.1) и оцененного уравнения
у = а + Ъху (7.2)
в доказательстве того, что b является несмещенной оценкой р и а — несмещенной оценкой ос, это условие не использовалось.
Это объясняется двумя причинами. Первая касается дисперсии оценок а и Ь. Желательно, чтобы она была как можно меньше, т.е. (в вероятностном смысX
Рис. 7.2. Модель с гетероскедастичным случайным членом
ле) обеспечивала максимальную точность. При отсутствии гетероскедастич-ности обычные коэффициенты регрессии имеют наиболее низкую дисперсию среди всех несмещенных оценок, являющихся линейными функциями от наблюдений у. Если имеет место гетероскедастичность, то оценки МНК, которые мы до сих пор использовали, неэффективны. Можно, по меньшей мере в принципе, найти другие оценки, которые имеют меньшую дисперсию и, тем не менее, являются несмещенными.
Вторая, не менее важная причина заключается в том, что сделанные оценки стандартных ошибок коэффициентов регрессии будут неверны. Они вычисляются на основе предположения о том, что распределение случайного члена гомоскедастично; если это не так, то они неверны. Вполне вероятно, что стандартные ошибки будут занижены, а следовательно, /-статистика — завышена, и будет получено неправильное представление о точности оценки уравнения регрессии. Возможно, вы решите, что коэффициент значимо отличается от нуля при данном уровне значимости, тогда как в действительности это не так.
Свойство неэффективности можно легко объяснить интуитивно. Предположим, что имеется гетероскедастичность типа, показанного на рис. 7.1 и 7.2. Наблюдение, для которого теоретическое распределение случайного члена имеет малое стандартное отклонение (как в наблюдении 7 на рис. 7.1), будет обычно находиться близко к линии регрессии у = а + рх и, следовательно, может стать хорошим направляющим ориентиром, указывающим место этой линии. В противоположность этому наблюдение, где теоретическое распределение имеет большое стандартное отклонение (как в наблюдении п на рис. 7.1), не сможет существенно помочь в определении местоположения линии регрессии. Обычный МНК не делает различия между качеством наблюдений, придавая одинаковые «веса» каждому из них независимо от того, является ли наблюдение хорошим или плохим для определения местоположения этой линии. Из этого следует, что, если мы сможем найти способ придания большего «веса» наблюдениям высокого качества и меньшего — наблюдениям низкого качества, мы, вероятно, получим более точные оценки. Другими словами, оценки для аир будут более эффективными. О том, как это делается, пойдет речь в разделе 7.4.
Возможные причины
Гетероскедастичность становится проблемой, когда значения переменных в уравнении регрессии значительно различаются в разных наблюдениях. Если истинная зависимость описывается уравнением (7.1) и изменения значений невключенных переменных, и ошибки измерения, влияя на случайный член, делают его сравнительно малым при малых у и х и сравнительно большим — при больших у и х, то экономические переменные часто совместно меняют свой масштаб.
Предположим, например, что вы пользуетесь моделью парной регрессии (7.1) для рассмотрения зависимости между государственными расходами на образование (у) и валовым внутренним продуктом (jc) в различных странах и вы сделали выборку наблюдений, представленных в табл. 7.1, включающую как малые страны, такие, как Сингапур, так и очень большие, такие, как США. Доля государственных расходов на образование в валовом внутреннем продукте обычно находится в диапазоне 3—9\%; по-видимому, отдельные страны уделяют больше внимания частному образованию, чем другие, или правительства одних стран в большей степени, чем правительства других, осознают необходимость образования1. По социальным или иным причинам та или иная страна тратит на образование долю ВВП, которая может колебаться в пределах до 3\% выше или ниже нормы. Очевидно, что при большом объеме ВВП изменение на 1\% его абсолютной величины будет выражаться значительно большими цифрами, чем при малом.
Гетероскедастичность может также появляться при анализе временных рядов. Если наблюдения, используемые для построения регрессии вида (7.1), представляют собой данные временного ряда и если х и у увеличиваются со временем, то может случиться, что и дисперсия случайного члена со временем тоже будет расти.
Обсуждение Введение в эконометрику
Комментарии, рецензии и отзывы
