Интерпретация коэффициентов множественной регрессии

Интерпретация коэффициентов множественной регрессии

Множественный регрессионный анализ позволяет разграничить влияние независимых переменных, допуская при этом возможность их коррелирован-ности. Коэффициент регрессии при каждой переменной*дает оценку ее влияния на величину у в случае неизменности влияния на нее всех остальных переменных х.

Это может быть продемонстрировано двумя способами. Один из них состоит в выяснении того, что если модель правильно специфицирована и выполнены условия Гаусса—Маркова, то оценки получаются несмещенными. Это будет сделано в следующей главе для случая, когда имеются только две независимые переменные. Второй способ состоит в оценивании регрессионной зависимости у от одной из независимых переменных, устранив перед этим возможность замещения этой переменной любой другой независимой переменной и показав далее, что оценка ее коэффициента в данном случае совпадет с оценкой коэффициента множественной регрессии. Этот способ будет описан для случая регрессии с двумя независимыми переменными. Предположим, что

у = а +р,дг, +р2х2 + и, (5.17) '

и допустим, что величины р, и Р2 положительны и х{ и х2 положительно кор-релированы.

Что произойдет, если оценить парную регрессию между у и По мере увеличения хх (1) у имеет тенденцию к росту, поскольку коэффициент р, положителен; (2) х2 имеет тенденцию к росту, так как х{ и х2 положительно коррели-рованы; (3) у получит ускорение из-за увеличения х2 и благодаря тому, что коэффициент Р2 положителен. Другими словами, изменения у будут преувеличивать влияние текущих значений хх, так как отчасти они будут связаны с изменениями х2.

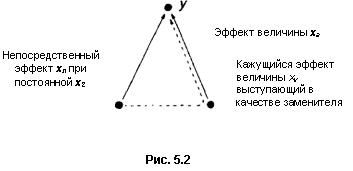
Это показано на рис. 5.2. Стрелки, проведенные сплошной линией, показывают непосредственные воздействия х{ и х2 на у. Если х2 не включается в рассмотрение, то часть изменений у за счет изменений х2 будет приписана х,, если переменная хх может замещать х2, действуя подобно ей. В результате оценка значения р, будет смещена. Расчет величины смещения будет представлен в разделе 6.2.

Предположим, однако, что вы устранили возможность замещения величиной х{ величины х2. Допустим, что можно разложить переменную х, на две составляющие:

х = х +£р (5.18)

где хх — составляющая, способная замещать х2, и 5q — оставшаяся часть. Парная регрессионная зависимость у от хх дает оценку влияния хх, не искаженного тем, что данная переменная частично выступает в качестве замещающей для х2. Мы покажем, что оценка рр полученная таким образом, является идентичной оценке коэффициента множественной регрессии (5.12).

Для регрессионной зависимости у от хх коэффициент наклона составит Ь,

где

г = Cov(x{,y) = Cov(xuy)-Cov(x{,y)

1 Var(3c!) Var(x!) + Var^) 2Cov(xj, jc,)' (5 *19)

так как xx равно (х,— x,).

Чтобы определить величину х1? можно оценить регрессию между х{ и х2 на основе данных об этих показателях, получив зависимость:

xl = c + dx2, (5.20)

Следовательно, величина х{ является составляющей х{, которая может быть спрогнозирована с помощью х2. Величина d определяется следующим выражением:

Соу(хьх2)

Подставляя формулу (5.20) в уравнение (5.19), получим:

£ Cov(xb)0-Cov({c + </x2},>0

1 Var(xj) + Var(c + dx2) 2Со v(x{, {с + dx2})

= Co(xhy)dCov(x2,y)

Var(x{) + d2 Var(x2) 2dCov(xj, x2)' (5 *22)

(Отметим, что с исключается из выражений ковариации и дисперсии, так как эта величина является постоянной.) Подставив выражение для d из соотношения (5.21) и перегруппировав члены, получим выражение для Ь{, представленное уравнением (5.12).

Итак, мы показали для случая с двумя переменными, что оценки множественной регрессии совершенно идентичны оценкам, которые мы могли бы получить при использовании двухэтапной процедуры с исключением перекрестных эффектов. Полученный результат может быть обобщен для случая к переменных.

Упражнения

Индекс относительной цены коммунальных услуг был получен путем деления неявного ценового дефлятора из табл. Б.2 на дефлятор общих расходов и умножения на 100. Оценка множественной регрессии между расходами на коммунальные услуги, располагаемым личным доходом и индексом относительных цен дает следующий результат:

j} =-43,4+ 0,18 be+0,137/?.

Дайте экономическую интерпретацию этого результата. Почему он не может вас удовлетворить?

Дополнение к упражнению 2.4. Оцените множественную регрессию между расходами на ваш товар, располагаемым личным доходом и индексом цен, построенным в упражнении 5.1, и дайте интерпретацию результатов.

Используя формулу (5.21), замените d в уравнении (5.22) и покажите, что можно получить выражение для Ь{, представленное уравнением (5.12).