2.6. интерпретация уравнения регрессии

2.6. интерпретация уравнения регрессии

Существуют два этапа интерпретации уравнения регрессии. Первый этап состоит в словесном истолковании уравнения так, чтобы это было понятно человеку, не являющемуся специалистом в области статистики. На втором этапе необходимо решить, следует ли ограничиться этим или провести более детальное исследование зависимости.

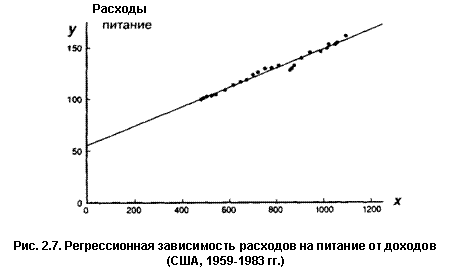
Оба этапа чрезвычайно важны. Второй этап мы рассмотрим несколько позже, а пока обратим основное внимание на первый этап. Это будет проиллюстрировано моделью регрессии для функции спроса, т. е. регрессией между расходами потребителя на питание (у) и располагаемым личным доходом (х) по данным, приведенным в табл. Б.1 для США за период с 1959 по 1983 г. Данные представлены в виде графика (рис. 2.7).

Предположим, что истинная модель описывается следующим выражением:

у = а+рх + и, (2.41)

и оценена регрессия

у = 55,3 + 0,093х. (2.42)

Полученный результат можно истолковать следующим образом. Коэффициент при х (коэффициент наклона) показывает, что если х увеличивается на одну единицу, то у возрастает на 0,093 единицы. Как х, так и у измеряются в миллиардах долларов в постоянных ценах; таким образом, коэффициент наклона показывает, что если доход увеличивается на 1 млрд. долл., то расходы на питание возрастают на 93 млн. долл. Другими словами, из каждого дополнительного доллара дохода 9,3 цента будут израсходованы на питание.

Доход

Что можно сказать о постоянной в уравнении? Формально говоря, она показывает прогнозируемый уровень^, когдах = 0. Иногда это имеет ясный смысл, иногда нет. Если* = 0 находится достаточно далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам; даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантии, что так же будет при экстраполяции влево или вправо.

В рассматриваемом случае экстраполяция к вертикальной оси приводит к выводу о том, что если доход был бы равен нулю, то расходы на питание составили бы 55,3 млрд. долл. Такое толкование может быть правдоподобным в отношении отдельного человека, так как он может израсходовать на питание накопленные или одолженные средства. Однако оно не имеет никакого смысла применительно к совокупности. В данном случае константа выполняет единственную функцию: она позволяет определить положение линии регрессии на графике. Пример постоянной, которая имеет ясный смысл, приведен в упражнении 2.1.

При интерпретации уравнения регрессии чрезвычайно важно помнить о трех вещах. Во-первых, а является лишь оценкой a, a b — оценкой р. Поэтому вся интерпретация в действительности представляет собой лишь оценку. Во-вторых, уравнение регрессии отражает только общую тенденцию для выборки. При этом каждое отдельное наблюдение подвержено воздействию случайностей. В-третьих, верность интерпретации зависит от правильности спецификации уравнения.

В сущности, мы построили довольно наивную зависимость для функции спроса. Мы будем неоднократно возвращаться к этому в следующих разделах, уточняя как определение, так и статистические методы, используемые для оценки коэффициентов уравнения. В то же время читателю рекомендуется, начиная с упражнения 2.4, проводить параллельные эксперименты для определения функций спроса для других товаров, представленных в табл. Б.1.

После оценивания регрессии возникает следующий вопрос: существуют ли какие-либо средства определения точности оценок? Этот очень важный вопрос будет рассмотрен в следующем разделе. Мы же сначала рассмотрим более подробно роль остаточного члена и его влияние на оценки аир.

Интерпретация линейного уравнения регрессии

Представим простой способ интерпретации коэффициентов линейного уравнения регрессии

у = a + Ьх,

когда у их — переменные с простыми, естественными единицами измерения.

Во-первых, можно сказать, что увеличение х на одну единицу (в единицах измерения переменной х) приведет к увеличению значения .у на b единиц (в единицах измерения переменной у). Вторым шагом является проверка, каковы действительно единицы измерения х и у, и замена слова «единица» фактическим количеством. Третьим шагом является проверка возможности более простого выражения результата, который может оказаться не вполне удобным. В примере, приведенном в данном разделе, в качестве единицы измерения для х и у использовались миллиарды долларов, что позволило произвести очевидные упрощения.

Постоянная а дает прогнозируемое значение>> (в единицах^), если х = 0. Это может иметь или не иметь ясного смысла в зависимости от конкретной ситуации.

Упражнения^

2.1. Регрессионная зависимость расходов на питание >> (основанная на тех же

данных, на которых уже строилась описанная в тексте функция спроса) от времени, определенного как f = 1 для 1959 г., t = 2 для 1960 г. и т.д., задана уравнением:

у = 95,3 + 2,53/.

Интерпретируйте результаты оценивания регрессии и сравните их с аналогичными результатами в случае с моделью регрессии для функции спроса, рассматриваемой в тексте. Обратите внимание, что в данном случае постоянная имеет простое толкование.

1 Упражнение 2.4 особенно важно в том смысле, что оно начинает серию регрессий для функций спроса, которые будут оцениваться читателем на протяжении всей книги. Если это упражнение выполняется группой студентов, то преподаватель должен дать студентам задания с разными товарами. Более подробную информацию об имеющихся данных можно получить в приложении Б.

2.2. Регрессионная зависимость расходов на оплату жилья от располагаемого личного дохода в соответствии с табл. Б.І, где обе величины измерены в миллиардах долларов за период с 1959 по 1983 г., может быть формализована в виде:

>> = -27,6 + 0,178х.

Регрессионная зависимость расходов на оплату жилья от времени, определенная так же, как в упражнении 2.1, может быть представлена таким образом:

9 = 48,9 + 4,84г.

Дайте экономическое толкование этих регрессий. Они предполагают различные объяснения для одних и тех же данных по переменной у. В какой степени они могут быть согласованы?

Постройте уравнение регрессии между р и е по данным из упражнения 1.3, сначала используя все 12 наблюдений, а затем исключив наблюдение для Японии, и дайте экономическую интерпретацию1.

В табл. Б.1 приведены ежегодные данные о потребительских расходах и располагаемых личных доходах для США на период с 1959 по 1983 г. Выберите один товар — не продукты питания и не жилье, — обозначьте его как у и оцените регрессию между у и х, где х — располагаемый личный доход, используя данные за 25 лет. Дайте интерпретацию коэффициентов регрессии2.

Оцените регрессии между характеристиками товара и временем, как это сделано в упражнении 2.1. Дайте соответствующую интерпретацию и сравните ее с интерпретацией регрессии, полученной в упражнении 2.4.

Два человека строят временной тренд для одного и того же набора из 25 наблюдений переменной у, используя модель:

у = а + р/ + и,

где t — время (последовательно принимающее значения от 1 до 25), aw — случайный член. Первый получает уравнение:

9 = 6,70+ 1,79/.

Второй по ошибке оценивает регрессию между їиуи приходит к такому уравнению:

t = -0,25 +0,44у. Из этого уравнения он получает:

j> = 0,57 + 2,27г.

Объясните наличие расхождения между данным уравнением и уравнением, полученным первым исследователем.

Как изменился бы результат оценивания регрессии в упражнении 2.1, если бы в качестве / использовались фактические даты (1959—1983 гг.), а не числа от 1 до 25?

1 Не следует начинать вычисление коэффициентов регрессии сначала, так как вы уже выполнили большую часть арифметических расчетов в упражнении 1.3.

2 Преподавателю необходимо иметь в виду, что если это групповое занятие, то учащимся следует дать задания оценить регрессию для разных видов товаров, помимо продуктов питания и жилья.

2.8. Исследователь изучает зависимость между совокупным спросом на услуги (у) и совокупным располагаемым личным доходом (х) по данным для американской экономики (обе величины измерены в миллиардах долларов в постоянных ценах), используя ежегодные данные временных рядов и модель:

у = а + рх + и.

Исследователь получает уравнение, проводя регрессионный анализ с помощью обычного метода наименьших квадратов. Предполагая, что обе величины у и х могут быть существенно занижены в системе национальных счетов из-за стремления людей уклониться от уплаты налогов, исследователь принимает два альтернативных метода уточнения заниженных оценок.

Исследователь добавляет в каждом году 90 млрд. долл. к показателю у и 200 млрд. долл. к показателю х.

Исследователь увеличивает значения как для х, так и для у на 10\% за каждый год.

Оцените влияние корректировок (2) и (3) на результаты оценивания регрессии.

2.9. Исследователь имеет ежегодные данные о временных рядах для совокупной заработной платы (W), совокупной прибыли (П), и совокупного дохода (Y)

для страны за период в п лет. По определению

Y= W+ П.

Используя обычный метод наименьших квадратов, получаем уравнение регрессии:

ft = b0 + bxY.

Покажите, что коэффициенты регрессии будут автоматически удовлетворять следующим уравнениям:

0| +ЬХ = 1; а0 + Ь0 = 0.

Объясните на интуитивном уровне, почему это должно быть именно так.

2.10. Исследователь считает, что в нестохастической части истинной модели

у пропорционален х:

у = рх + и.

Выведите на основании исходных принципов формулу для Ь, оценки МНК для Ъ. Покажите, что в этом случае (2.31) можно записать в следующем виде:

S = Ъу] + ЬгЪх} 2Ь^хіУі,

и что, следовательно,

b = ^xiyi /Ъх].

2.11. Выведите из исходных предпосылок оценку МНК для а в модели:

у = а + и.

Другими словами, у представляет собой просто сумму постоянной величины и случайного члена. Снова вначале определите 5, а затем продифференцируйте.