7.6. обнаружение автокорреляции первого порядка: критерий дарбина—уотсона
7.6. обнаружение автокорреляции первого порядка: критерий дарбина—уотсона
Начнем с частного случая, в котором автокорреляция подчиняется авторегрессионной схеме первого порядка:
w,= pw,_, + є,. (7.21)
Это означает, что величина случайного члена в любом наблюдении равна его значению в предшествующем наблюдении (т. е. его значению в период t — 1), умноженному на pf, плюс новый єг Данная схема оказывается авторегрессионной, поскольку и определяется значениями этой же самой величины с запаздыванием, и схемой первого порядка, потому что в этом простом случае максимальное запаздывание равно единице. Предполагается, что значение є в каждом наблюдении не зависит от его значений во всех других наблюдениях. Если р положительно, то автокорреляция положительная; если р отрицательно, то автокорреляция отрицательная. Если р = 0, то автокорреляции нет и третье условие Гаусса—Маркова удовлетворяется.
Конечно, мы не располагаем способом измерения значений случайного члена, поэтому мы не можем оценить регрессию (7.21) непосредственно. Тем не менее мы можем оценивать р путем оценивания регрессионной зависимости et от et_x с
Cov(e,4,e,)
использованием обычного МНК. При этом оценка р равна уаг^ {) '
Так как среднее значение Г остатков равно нулю, ет-i (среднее значение остатков в наблюдениях от 1 до Т— 1) и ет (среднее значение остатков в наблюдениях от 2 до Т) будут близки к нулю, если выборка достаточно велика, и Cov(eret_{) и Var (е,^) будут аппроксимироваться выражениями
jT^yZ«7-1*7 и y^7jZ^2-i» соответственно.
Cov(et_i,et) 2*ег-& yar^ ^ аппроксимируется выражением
Кроме того, £e,2_i будет приблизительно равно ^е]. Следовательно,
Широко известная статистика Дарбина—Уотсона (d) определяется следующим образом {:
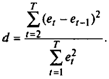 |
rf-*2-2p.
(7.22)
Если автокорреляция отсутствует, то р = 0, и поэтому величина должна быть близкой к двум. При наличии положительной автокорреляции величина d, вообще говоря, будет меньше двух; при отрицательной автокорреляции она, вообще говоря, будет превышать 2. Так как р должно находиться между значениями 1 и —1, то d должно лежать между 0 и 4.
Критическое значение d при любом данном уровне значимости зависит, как можно предполагать, от числа объясняющих переменных в уравнении регрессии и от количества наблюдений в выборке. К сожалению, оно также зависит от конкретных значений, принимаемых объясняющими переменными. Поэтому невозможно составить таблицу с указанием точных критических значений для всех возможных выборок, как это можно сделать для /и /-статистик; но можно вычислить верхнюю и нижнюю границы для критического значения d. Для положительной автокорреляции они обычно обозначаются как du и dL.
На рис. 7.5 данная ситуация представлена в виде схемы; стрелка указывает критический уровень d, который обозначается как d т. Если бы мы знали значение dKpum, то могли бы сравнить с ним значение а, рассчитанное для нашей регрессии. Если бы оказалось, что d>dKpum, то мы не смогли бы отклонить нулевую гипотезу от отсутствии автокорреляции. В случае d<dKpum мы бы отклонили нулевую гипотезу и сделали вывод о наличии положительной автокорреляции.
О 4 d d 2 d 4
W L КРИТ U *~ ^
Рис. 7.5. Тест Дарбина—Уотсона на автокорреляцию (показана зона неопределенности в случае предполагаемой положительной
автокорреляции)
Вместе с тем мы знаем только, что d m находится где-то между dL и dv. Это предполагает наличие трех возможностей:
1 В русскоязычной литературе эта статистика чаще обозначается как DW. {Прим. ред.) 220
Величина d меньше, чем dL. В этом случае она будет также меньше, чем d т, и поэтому мы сделаем вывод о наличии положительной автокорреляции.
Величина d больше, чем dv. В этом случае она также больше критического уровня, и поэтому мы не сможем отклонить нулевую гипотезу.
Величина d находится между dL и dv. В этом случае она может быть больше или меньше критического уровня. Поскольку нельзя определить, которая из двух возможностей налицо, мы не можем ни отклонить, ни принять нулевую гипотезу.
В случаях 1 и 2 тест Дарбина—Уотсона дает определенный ответ, но случай 3 относится к зоне невозможности принятия решения, и изменить создавшееся положение нельзя.
В табл. А.5 в конце книги даны значения (dL и dv), стоящие на пересечении строк и столбцов, соответствующих количеству наблюдений и числу объясняющих переменных для уровней значимости в 5 и 1\%. В таблице показаны критические значения в случае положительной автокорреляции, наиболее часто встречающемся в экономических моделях. Можно видеть, что чем больше число наблюдений, тем уже зона неопределенности, представленная отрезком между dL и dv.
*~<*и dKP„r *~dL
d 4
Рис. 7.6. Тест Дарбина—Уотсона на автокорреляцию (показана зона неопределенности в случае предполагаемой отрицательной
автокорреляции)
Проверка на отрицательную автокорреляцию проводится по аналогичной схеме, причем зона, содержащая критический уровень, расположена симметрично справа от 2. Так как отрицательная автокорреляция встречается относительно редко, предполагается, что при необходимости вы сами вычислите границы зоны на основе соответствующих значений для положительной автокорреляции при данном числе наблюдений и объясняющих переменных. Это достаточно легко сделать. Как показано на рис. 7.6, величина (4 — dv) есть нижний предел, ниже которого признается отсутствие автокорреляции, а (4 — dL) — верхний предел, выше которого делается вывод о наличии отрицательной автокорреляции.
Упражнения
Рассмотрите статистику Дарбина—Уотсона для логарифмической функции спроса, которую вы построили в упражнении 5.6. Есть ли там автокорреляция? Если да, то как это повлияло на результаты выполненных вами статистических тестов?
Если ваш регрессионный пакет позволяет распечатать остатки для уравнения регрессии, сделайте это для оцененных вами по МНК уравнений функции спроса. Подтверждает ли рассмотрение остатков наличие (или отсутствие) автокорреляции, на которую указывает статистика Дарбина—Уотсона? Можете ли вы дать экономическое объяснение поведения остатков?
Обсуждение Введение в эконометрику
Комментарии, рецензии и отзывы
