1.5. обратная функция
1.5. обратная функция

Рассмотрим функцию у = х2. Выберем у
произвольное значение у = b > 0. Этому
значению функции соответствуют два зна- b
чения аргумента х = — а и х = а на интерV
вале (—оо, +оо) и одно значение х = а на V.
интервале (0, +оо). ~а
Говорят, что функция у = х2 необрати-ма на интервале (—оо, +оо) и обратима на интервале (0, +оо).
Определение 1. Функция у = / (ж), определенная на промежутке X, называется обратимой на промежутке X, если любое свое значение она принимает только в одной точке этого промежутка; иными словами, если любым различным значениям аргумента соответствуют различные значения функции:
xi ф х2 =Ф f(xi) ф f(x2).
Если под промежутком X рассматривается область определения функции, то, говоря об обратимости функции, слова «на промежутке X» обычно опускают. Выражения «функция у = х2 необратима, а функция у = х обратима» означают, что функции являются необратимыми или обратимыми на своей области определения.
Теорема 1. Если функция у = f(x) строго монотонна на промежутке X, то она обратима на этом промежутке.
□ Пусть у = f(x) возрастает на X. Тогда из х < х<х следует f(xi) < f{x2)Таким образом, различным значениям аргумента соответствуют разные значения функции, т.е. функция обратима. ■
Наглядную иллюстрацию этой теоремы дает функция у = = х2. Она не является строго монотонной и необратима на своей области определения, но возрастает и обратима на интервале (0,+ос).
Определение 2. Пусть функция у = f(x) обратима на промежутке X и отображает X в Y. Поставим в соответствие каждому у из Y то единственное значение ж, при котором f(x) = у. Тогда получим функцию, которая определена на У, а область ее значений есть X. Эта функция называется обратной для функции / и обозначается
Из теоремы 1 следует, что для любой монотонной на X функции у = f(x) существует обратная функция. Чтобы найти ее, нужно из уравнения у = f(x) выразить х через у.
V Пример 1. Для функции у = х2, если ее областью определения считать всю числовую ось, нет однозначно определенной обратной функции. Причина заключается в том что, у = 4, например, принимает значение в двух точках х = 2 и х = —2, поэтому в точке у = 4 обратную функцию нельзя определить однозначно. Для ветви функции у = х2, определенной в интервале (0, оо), обратной функцией является у = л/х . Для функции у = х2, рассматриваемой на полупрямой (—оо, 0], обратной является функция у = —л/х. А
вал
7Г 7Г
ция у = arcsin х.
V Пример 2. Для определения однозначной «ветви» функции, обратной функции у = sin ж, выберем один из интервалов монотонности синуса. Обычно принято рассматривать интерв котором обратной для у = sin х является функАналогичным образом можно определить однозначные «ветви» функций, обратных функциям у = cos ж, у = tg ж, у = ctg х. А
Построение графика обратной функции
у
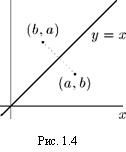 |
Весь анализ бесконечных вращается вокруг переменных величин и их функций.
Л. Эйлер
Обсуждение Математика для социологов и экономистов
Комментарии, рецензии и отзывы
