12.2. понятие определенного интеграла
12.2. понятие определенного интеграла
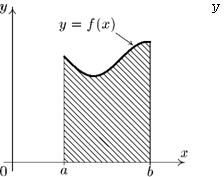
Рассмотрим непрерывную функцию у = /(ж), не принимающую отрицательных значений, так что график ее целиком лежит выше оси Ож, хотя и может касаться оси Ох в некоторых точках. Пусть а и b — такие числа, что функция определена при а ^ х ^ Ь.
Кривая у = f(x) и прямые х — а. х — b w у = 0 ограничивают некоторую область плоскости, называемую областью под кривой у = f(x) от а до 6, или криволинейной трапецией.
Если требуется вычислить площадь S криволинейной трапеции, то можно, например, покрыть плоскость сетью мелких квадратов и сосчитать число квадратов, лежащих внутри нашей области (рис. 12.1). Это не дает еще всей площади, поскольку некоторые из квадратов лежат частично внутри, а частично вне рассматриваемой области. Но если сделать сеть достаточно густой, то можно вычислить S с любой степенью точности.
О
Рис. 12.1. Криволинейная трапеция
 Можно вычислить площадь криволинейной трапеции и с помощью тонких прямоугольников. Лейбниц считал, что криволинейная трапеция составлена из бесконечно тонких прямоугольников (рис. 12.2). Каждый такой прямоугольник поднимается над точкой х интервала [а, 6]; он имеет высоту f(x) и бесконечно
Можно вычислить площадь криволинейной трапеции и с помощью тонких прямоугольников. Лейбниц считал, что криволинейная трапеция составлена из бесконечно тонких прямоугольников (рис. 12.2). Каждый такой прямоугольник поднимается над точкой х интервала [а, 6]; он имеет высоту f(x) и бесконечно
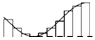 |
/(*)
f(Ci)
a dx
О
a Axj
Рис. 12.2. Вычисление площади криволинейной трапеции
малую ширину dx; площадь его равна, следовательно, f(x)dx. Общая же площадь S есть сумма всех таких площадей.
Напомним, Лейбниц писал S = J f(x) dx. Символ J означал у
него сумму. Этот символ происходит от удлинения буквы S (первой буква слова Summa). Позже ученик Лейбница Иоган Бернул-ли предложил отличать «целостную сумму бесконечно малых» от обычной суммы и предложил знак J именовать интегралом от
латинского слова integralis (целостный).
Фурье усовершенствовал обозначение Лейбница, предложив явно указывать начальное и конечное значения х:
S =
f(x)dx.
Рассуждения математиков XIX века носили нестрогий характер. Термин бесконечно малая величина не был достаточно строго определен, что приводило к противоречиям. Строгое определение основано на понятии предела и интегральной суммы. Оно вобрало в себя качественный смысл определения Лейбница и устранило нечеткость формулировок.
Пусть функция f(x) неотрицательна на [а, Ь]. Разобьем отрезок [а, Ь] на п промежутков точками жо, жъ ..., жп:
а = хо < х < Х2 < ... < xn-i < хп = Ь.
На каждом отрезке разбиения выберем точку С{ и положим
Дж^ — Х{ Х{—,
г = 1, 2, ... , п.
Тогда произведение f(ci) Ах і равно площади прямоугольника Si со сторонами f(ci) и Ах і. Сумма площадей всех таких прямоугольников равна сумме вида
п
Эта сумма представляет площадь ступенчатой фигуры. Чем уже ступеньки, тем ближе площадь ступенчатой фигуры к площади криволинейной трапеции (рис. 12.2). Естественно ожидать, что при неограниченном возрастании числа промежутков, так что наибольшая из их длин стремится к нулю, сумма Sn стремится к площади криволинейной трапеции S. Введем теперь точное определение.
Пусть на отрезке [а, ь] задана функция у = f(x) (теперь уже не обязательно неотрицательная). Разобьем отрезок [а, ь] на п промежутков точками х$, х, ..., хп
а = Xq < х < Х2 < ... < хп-1 < хп = ь.
На каждом отрезке разбиения [#г-ъ xi] выберем точку С{ и положим
Ах і — х{ Хі—і, і — . 2, п. Сумму вида
п
Sn = Y,f(Ci)Axi
і=1
назовем интегральной суммой для функции у = f(x) на [а, ь]. Очевидно, что интегральная сумма зависит от способа разбиения отрезка [а, ь] точками #о, #ъ •••5 хп, так и от выбора точек со, сі, сп на каждом из промежутков разбиения [#г-ъ хі], і — = 1,2,..., п.
Обозначим через max Ахі максимальную из длин отрезков [хі-і, Xi], где і = 1, 2, ..., п.
Определение. Пусть предел интегральной суммы
п
Sn = Y,f(ci)^Xi
i=l
при стремлении max Ахі к нулю существует, конечен и не зависит от способа выбора точек х, Х2, и с, С2, .... Тогда этот предел называется определенным интегралом от функции у = f(x)
8 Я. М. Ахтямов
на [а, Ь] и обозначается
f(x)dx,
а сама функция у = f(x) называется интегрируемой на отрезке [а, Ь], т. е.
f(x)dx= lim У*/(с*)Дж*.
max Дж; —>-0 .—: г=1
Эта запись читается: «интеграл от а до бэ эф от икс дэ икс». При этом число а называется нижним пределом, число b — его верхним пределом («пределы интегрирования» не имеют ничего общего с термином «предел функции»); функция f(x) — подынтегральной функцией, выражение f(x)dx — подынтегральным
b
выражением, а задача о нахождении J f(x) dx — интегрированиа
ем функции f(x) на отрезке [а, Ь].
Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы существенно различные понятия. Неопределенный интеграл представляет функцию (а точнее семейство функций), а определенный интеграл — это число.
Из определения следует, что величина определенного интеграла не зависит от обозначения переменной интегрирования, т. е.
f(x)dx =
/(*) dt =
f(u)du.
Верхний предел b может быть больше или меньше нижнего а. В первом случае
а = xq < х < Х2 < ... < xn-i < хп = Ь, т. е. Ахі = х{ — х{> 0. Во втором случае
а = хо > х > Х2 > ... > xn-i > хп = Ь, т. е. Ахі = х{ — х{< 0.
Поэтому по определению полагают
| ( | 1 | Ь |
| f(x)dx = - | f(x)dx. | |
| 1 | ) с | і |
Понятие определенного интеграла распространяют и на случай а = 6; интеграл с равными пределами считается равным нулю:
а
f(x)dx = 0.
а
Это соглашение оправдано тем, что интегральная сумма стремится к нулю при сближении а и Ь.
Очевидно, если функция f(x) интегрируема на отрезке [а, 6], то она и ограничена на этом отрезке. В самом деле, если f(x) не ограничена на отрезке [а, 6], то она не ограничена на некотором отрезке [#г-ъ хгЗа счет выбора точки сі интегральную сумму можно сделать сколь угодно большой, а такая интегральная сумма не имеет конечного предела, что противоречит определению, согласно которому предел интегральной суммы Sn существует и конечен.
Покажем на примере функции Дирихле, что обратное утверждение неверно: существует ограниченная функция, не являющаяся интегрируемой. Напомним, что функция Дирихле равна единице в рациональных точках и нулю — в иррациональных. На любом отрезке [а, Ь] эта функция ограничена, но не является интегрируемой на нем. Действительно, если в каждом отрезке [#г-ъ хг выбрать рациональную точку сі, то интегральная сумма
п п п
г=1 г=1 г=1
= (xi х0) + (х2 xi) + ... + (xn-i хп-2) + (хп xn-i) =
= хп — хо = b — а. Если выбрать иррациональную точку то f(ci) = 0 и
п п п
sn = Y, f(a) Ахі = Е0 • ахі = Е0 = °г=1 г=1 г=1
Таким образом, с одной стороны Sn = b — а, с другой стороны Sn = 0. Поэтому предел интегральных сумм не существует и функция Дирихле не является интегрируемой.
Отметим без доказательств, что справедливы следующие утверждения:
Если функция f(x) интегрируема на отрезке [а, 6], то она интегрируема на любом отрезке [с, of], содержащимся в [а, 6].
Если функция f(x) непрерывна на отрезке [а, 6], то она интегрируема на этом отрезке.
Если функция f(x) имеет на отрезке [а, Ь] конечное число точек разрыва первого рода, то она интегрируема на [а, Ь].
Обсуждение Математика для социологов и экономистов
Комментарии, рецензии и отзывы
