14.5. касательная плоскость и нормаль к поверхности

14.5. касательная плоскость и нормаль к поверхности

В п. 7.1 было дано определение касательной к кривой как предельного положения секущей.

Похожим образом определяется касательная плоскость.

Плоскость, проходящая через точку Mq поверхности, называется касательной плоскостью в данной точке, если угол между этой плоскостью и секущей, проходящей через точку Мо и любую точку поверхности, стремится к нулю, когда точка М стремится по этой поверхности к точке Mq.

Непрерывность функции нескольких переменных проверить напрямую бывает довольно трудно, но это важное свойство функции можно установить более простым способом — воспользовавшись следующим утверждением: если функция z = /(ж, у) имеет непрерывные частные производные в точке Mq, то она непрерывна в этой точке и, более того, имеет в этой точке касательную. Как видим, это утверждение, которое мы примем без доказательства, позволяет также проверять существование касательной плоскости к поверхности.

10 Я. М. Ахтямов

Если поверхность задана уравнением z = f(x, у), то уравнение касательной плоскости в точке Мо(жо? уо, zq) к данной поверхности дается уравнением:

z ~ zo = f'x(xo, Уо) (х х0) + fy{x0, уо) (у Уо),

а канонические уравнения нормали, проведенной через точку

Мо(жо, Уо, zo) поверхности, имеет следующий вид:

х хо у уо z Zo

Ґх(хо, У о) Ґу(хо, у о) -1

В случае, когда уравнение гладкой поверхности задано в неявном виде

F(x, у, z) = 0,

уравнение касательной плоскости в точке Мо(жо? Уо, zo) поверхности имеет вид

F'x(xo, уо, zo) (х х0) + Fy(x0, у0, z0) (у Уо) +

+ F'z(x0, уо, zo) (z zo) = 0,

а канонические уравнения нормали, проведенной через точку Мо(жо, Уо, zo) поверхности:

х Xq _ у уо _ z Zo

F'x(xo, уо, zo) F'y(xo, уо, z0) F'z(x0, y0, z0)'

V Пример 1. Найти уравнения касательной плоскости и нормали к поверхности z = х2 + у2 + 1 в точке Мо(1, 0, 2).

Решение. Вычисляем /^.(1, 0) и fy(l, 0):

f'x(x,y) = 2x, /4(1, 0) = 2-1 = 2,

ft(x,y) = 2y, /£(1,0) = 2-0 = 0.

Отсюда получаем уравнение касательной плоскости в точке Мо(1, 0, 2) к данной поверхности

*-2 = 2-(ж-1) + 0-(у-0),

или

z = 2 х

и канонические уравнения нормали, проведенной через точку Мо(жо, Уо, zo) поверхности:

х I _ у -0 _ z 2 2 ~ 0 ~ -1 ' А

V Пример 2. Найти уравнения касательной плоскости и нормали к поверхности F(x, у, z) = х3 + у3 + z3 + х у z — 6 в точке М0(1, 2, -1).

Решение. Вычисляем fx(l, 0) и /^(1, 0):

Fx(x, y,z) = 3x2 + yz F^(l, 2, -1) = 1,

F^(x, у, = 3 у2 + ж z, F^(l, 2, -1) = 11,

F^(x, у, z) = 3z2 + yx, F^(l, 2, -1) = 5.

Отсюда получаем уравнение касательной плоскости в точке Мо(1, 0, 2) к данной поверхности

(ж-1) + 11(у-2) + 5(* + 1) = 0

и канонические уравнения нормали, проведенной через точку Мо(#о, 2/0•> ^о) поверхности:

ж-1_у-2_^ + 1 1 ~ 11 ~ 5 А

Задача. Найти уравнение касательной плоскости и уравнение нормали к поверхности z = х2 + Зу2 в точке Mq(—2, 1, 7).

Ответ: Уравнение касательной

4ж 6у + г + 7 = 0,

а уравнение нормали

x + 2_y-l_z-7 -4 ~ 6 ~ -1

14.6. Производная сложной функции

Предположим, что имеется данная функция z двух переменных и и V.

z = f(u, v),

причем эти переменные суть функции переменных ж, у, т. е. и = д{х, у), v = h(x, у).

Формула

z = f{g(x, у), h(x, у)) определяет сложную функцию.

Можно доказать, что если функции z, и и v дифференцируемы, то

dz _ dz du ^ dz dv ^ dx du дх dv dx1

dz _ dz ди dz dv ду ди ду dv ду

V Пример. Найти первые частные производные функции z = (5х у) п(х2 + у2).

Решение. Введем обозначения: и = 5 х — у, v = х2 + у2; тогда z = и v. Поэтому

dz dz ди dz dv . и п

7^— = 7^— • Ь тт— • тт— = In • 5 Ч 2х =

ох ди дх dv дх v

= 5п(х2 + у2) + 2х^—^,

dz dz du dz dv Л ( л. и _ ду ди ду dv ду v

т/9 9ч ^ Б х — у

= _1п (х2 + у2 ) + 2у^г-А1. к

x +У

В частности, если и и v — функции только одной переменной ж, и, следовательно, и = g(x), v = h(x), то z = f(u, v) = = f(g(x), h(x)) = Z(x). Откуда получаем

dz _ dz du dz dv

dx du dx dv dx

Ho

dz _ dz du _ du dv _ dv

dx dx' dx dx^ dx dx

Следовательно,

dz _ dz du dz dv ^ dx du dx dv dx

14.7. Производная по направлению. Градиент

Пусть функция z = f(x,y) определена в некоторой окрестности точки Мо(жо, 2/о); ^ — некоторый луч с началом Mq; М(х,у) — точка на этом луче, принадлежащая рассмариваемой окрестности

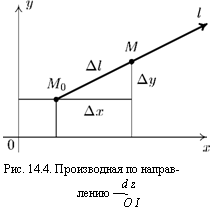А1

ДМ) /(Мо)

lim

то этот предел называется производной функции

z = /(ж, у) по направлению I

dz

в точке Mq и обозначается

(читается «дэ зет по эль»);

здесь / — вектор, имеющий направление луча /.

В частности, частная производ-д z

ная — есть производная z = f(x,y)

по положительному направлению оси д z

Ох, а —— — производная по положи-ду

тельному направлению оси Оу.

Не ограничивая общности рассу-

У

о

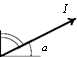
Рис. 14.5. Единичный вектор I

ждений, можно считать, что / — единичный вектор; тогда он имеет координаты (cos се, sin се) или, что то же самое, (cos a, cos /3),

где а, (3 — углы между / и положительными направлениями осей Ох, Оу соответственно (рис. 14.5).

Теорема. Если функия z = f(x,y) имеет в точке Mq(xo, уо) непрерывные частные производные, то в этой точке существу0 z ~* ет производная — по любому направлению I = (cos a, cos (3),

причем

dz dz dz п

— = — cos а + — cos р, ol ох оу

(14.2)

где

— значения частных производных в точке

dz dz dx dy М0(жо,г/о).

Производная по направлению характеризует скорость изменения функции z = f(x,y) в точке Мо(хо,уо) по направле-—*

нию /. В этом состоит механический смысл производной по направлению. Геометрический смысл производной по направлению состоит в том, что она выражает величину наклона функции в направлении. В экономическом смысле производная по направлению от производственной функции есть количество продукции, приходящееся на единицу определенной линейной комбинации факторов.

Рассмотрим вектор а = [ тг-? тг)Тогда скалярное произдх dy)

ведение вектора а на вектор / = (cos се, cos j3) выражается формулой

- dz dz а I = —— cos а + — cos p. ox oy

Сопоставляя последнюю формулу с равенством (14.2), получим

dz m=aL

С другой стороны, а I = a\l cos if, где tp — угол между векторами а и /. Это скалярное произведение имеет максимальное значение при cosy? = 1, т. е. при у? = 0. Таким образом, наиболь-

шее значение

dz

dl

d z d z

достигается в направлении / = ( ——, ——

ox oy

f dz dz

Вектор с координатами ——, —— , характиризующии наох оу)

правление максимального роста функции z = /(ж, у) в точке Мо(жо, Уо)5 называется градиентом функции z = / (ж, у) в этой точке и обозначается grad z или Vz.

Градиент совпадает с нормалью к линии уровня /(ж, у) = = const в точке Mq.

Понятие «градиент» Дж. Максвеллом; ему же принадлежит и обозначение grad. Оно происходит от латинского слова gradior (градиор), означающего «расти» (или от латинского слова gradients (градиентис), означающее «шагающий»). Обозначение V — перевернутую греческую букву А (дельта) — придумал Р. Гамильтон. Этот значок теперь называют «набла» (из-за сходства с остовом древнего музыкального инструмента наблы).

МАКСВЕЛЛ (Maxwell) Джеймс Клерк (1831-1879) — английский физик, создатель классической электродинамики, один из основателей статистической физики, способствовал формированию векто-роного исчисления в виде отдельной математической дисциплины. Стал членом Лондонского королевского общества в 29 лет.

ГАМИЛЬТОН (Hamilton) Уильям Роуан (1805-1865) — ирландский математик и астроном, член Ирландской королевской Академии наук. В 22 года — профессор астрономии в Дублинском университете и директор университетской астрономической обсерватории. В его работах дано точное формальное изложение теории комплексных чисел. В механике Гамильтон применил вариационный метод (так называемый принцип наименьшего действия).

Итак, градиент

grad, = V,= l,-, Ту)

характеризует направление наибольшей скорости изменения функции. В этом состоит механический смысл градиента. С геометрической точки зрения градиент выражает направление наибольшего наклона графика функции, а с экономической — такую линейную комбинацию факторов х и у, при которой наблюдается наибольший выход продукции на единицу этого состава.

Производная функции z = f(x,y) в направлении / и градиент связаны соотношением

14.8. Частные производные высших порядков

Частными производными второго порядка называют частные производные, взятые от частных производных первого порядка:

d2z д (dz ^„

дх2 дх дх d2z д f dz

_ z"

ду2 ду ду d2z д f dz

дх ду ду дх d2z д [dz

ду дх дх ду

ух •

d2z d2z Обозначение —^ читается «дэ зет по дэ икс квадрат», а —^~ дх дхду

читается «дэ зет по дэ икс дэ игрек».

Аналогично определяются частные производные третьего и более высоких порядков. Запись

dnz дхкдуп~к

означает, что функция z продифференцирована к раз по переменной х и п — к раз по переменной у.

Частные производные zxy и z'yX называются смешанными. Значения смешанных производных равны в тех точках, в которых эти производные непрерывны.

V Пример 1. Найти вторые частные производные функции z = хА + 5 Xі у2 + 6 х у + 5. Убедиться в том, что zxy = ZyX .

Решение. Вначале находим первые частные производные данной функции:

z'x = 4 ж3 + 10 х у2 + 6 г/, z'y = 10 х2 у + 6 х.

Дифференцируя каждую из полученных производных по х и по у, находим вторые частные производные данной функции:

zxx = 12 ж2+ 10 у2

4^ = 20^1/+ 6,

Zyy — 10 х ,

4'я = 20жу + 6.

Смешанные частные производные равны:

zxy = z'yx = 20 х У + 6А

Задача 1. Найти смешанные частные производные функции z = х3 у2 + х sin у и показать, что они равны между собой.

Ответ: zxy = zfyX = 6 х2 у + cos у.