14.9. производная неявной функции от одной переменной

14.9. производная неявной функции от одной переменной

В социально-экономических исследованиях часто возникает ситуация, когда значения двух переменных х и у связаны между собой уравнением, которое, если все члены перенести налево,

в общем случае имеет вид

F(x,y)=0. (14.3)

Здесь F(x,y) есть функция двух переменных, заданная в какой-либо области. Если для каждого значения х из некоторого промежутка существует одно или несколько значений у, которое совместно с х удовлетворяют уранению (14.3), то этим определяется, однозначная или многозначная, функция у = f(x), для которой равенство

F(x,f(x)) = 0 (14.4)

имеет место уже тождественно относительно X. Рассмотрим, например, уравнение

х2 + у2-1 = 0.

Уравнение определяет двузначную функцию от ж в промежутке [—1,1], а именно

у = J — х2 .

Если вместо у подставить эту функцию в уравнение (14.3), то получится тождество.

Здесь удалось найти для у очень простое аналитическое выражение через х, даже в элементарных функциях. Однако так обстоит дело не всегда. Например, если взять уравнение

у — х — є sin у = О (0 < є < 1),

то этим уравнением переменная у не выражается в конечном виде через элементарные функции от х.

Функция у = f(x) называется неявной, если она задана посредством неразрешенного (относительно у) уравнения (14.3); она становится явной, если рассматривается непосредственная зависимость у от х. Ясно, что эти термины характеризуют лишь способ задания функции у = f(x) и не имеют отношения к ее природе.

В простейшем случае, когда уравнение (14.3) — алгебраическое, т. е. когда функция F(x,y) есть полином относительно х и у, определяемое им неявная функция у от х (вообще многозначная) называется алгебраической. Если степень уравнения (относительно у) не выше четырех, то алгебраическая функция допускает явное выражение в радикалах; при степени выше четырех такое выражение возможно лишь в виде исключения.

Полезна следующая

Теорема. Пусть для функции F(x,y) выполнены следующие условия:

F(x,y) определена и непрерывна в прямоугольнике

D = [х0 А, х0 + А; у0 А7, у0 + А7]

с центром в точке (жо, У о) 5

частные производные F'x и F'y существуют и непрерывны в D]

F(x0,y0)=0;

производная F'y{x^, уо) отлична от нуля.

Тогда в некоторой окрестности точки (жо,уо) уравнение (14.3) определяет у как однозначную функцию у = f(x), которая имеет непрерывную производную у'х] при х = xq эта функция принимает значение у о.

Теорема однако не дает представления о способе вычисления производной от неявной функции у'х. А это очень важно в социально-экономических исследованиях, так как использование производной позволяет более детально исследовать функцию: определить интервалы ее возрастания и убывания, найти точки минимума и максимума. Поэтому ниже приводится простой прием, с помощью которого можно легко находить производную от неявной функции.

Пусть выполнены условия теоремы. Согласно определению неявной функции у = f(x) удовлетворяет уравнению (14.3). Левая часть этого уравнения представляет собой сложную функцию от ж, которая тождественно равна нулю. Тогда и производная ее по х также есть нуль. Воспользовавшись формулой (14.1) дифференцирования сложной функции, получаем

dF^_dF^ d^+dF_ dy__dF^+dF_ dy_ dx dx dx dy dx dx dy dx

Так как производная правой части (14.3) равна нулю, а производdF

ная левой части равна ——, то имеем

dx

dF dF dy ^

1 • — — ().

дх ду dx '

или, в других обозначениях,

К + Ку'х = 0, (14-5)

откуда (так как F'

Ф 0) имеем

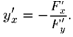
(14.6)

Эта формула выражает правило дифференцирования неявной функции у от переменной х.

Если функция F(x,y) имеет еще и непрерывные производные второго порядка, то выражение, стоящее в равенстве (14.6) справа, может быть продифференцировано по ж, следовательно существует и вторая производная ухх от неявной функции у.

После того как факт второй производной установлен, их вычисление производится путем повторного дифференцирования тождества (14.5) с учетом того, что у является функцией от х. Дифференцирование тождества (14.5) дает

р" + . у' і (р" +f" .у'.у' + F' • v" = 0

± хх * ± ху Ух * Vі ху * ± уу Ух) Ух * у Ухх

откуда (так как F' ф 0) имеем

V Пример. Неявная функция задана уравнением

Решение. Дифференцируя последовательно по х (причем у считаем функцией от ж), получим

х + УУ' _ ху' -у

х2 + у2 ~ х2 + у2

или

х + уу'

ху у;

затем

1 + Ы)2 + Уу" = ху".

Из первого уравнения находим

из второго (если подставить найденное значение у1)

/ = !±^ = 2^±4. ▲

х-у (х-у)

Задача. Неявная функция задана уравнением F(x, у) = ху ух = 0, {хфу).

Найти

ах

Ответ: ^ = -^(1 -]ПХ).

dx xz(l- y)