Глава 2 элементарные функции 2.1. основные элементарные функции

Глава 2 элементарные функции 2.1. основные элементарные функции

Прежде чем ввести необходимые определения отметим, что функции, называемые элементарными, были первыми функциями, которые подверглись математиками наиболее детальному изучению и начали широко использоваться в приложениях математики. Их особая роль в математическом анализе объясняется тем, что они обладают рядом важных свойств. Забегая вперед приведем два наиболее важных из них: 1) всякая элементарная функция непрерывна на своей области определения; 2) производная от элементарной функции есть также элементарная функция.

К основным элементарным функциям относят пять классов функций:

степенные у = ха (а — действительное число);

показательные у = ах, а ^ 1, а > 0;

логарифмические у = ogax, а ф 1, а > 0;

тригонометрические: у = sin ж, у = cos ж, у = tg ж, у= ctg х;

обратные тригонометрические: у = arcsinx, у = arccosx, у = arctgx, у = arcctgx.

Приведем в качестве справочного материала их свойства и графики.

2.1. Основные элементарные функции

31

1) степенные функции:

1. у = х°:

D(/) = (-oo, 0)U(0, +оо);

E(f) = {1};

четная: (—ж) = ж ;

постоянна на (—оо, 0) U (0, +оо);

ограниченная;

непериодическая.

Рис. 2.1

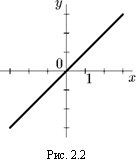2. у = х:

£>(/) = (-оо, +оо);

E(f) = (-оо, +оо);

нечетная: (—ж)1 = —ж1;

возрастает на (—оо, +оо);

неограниченная;

непериодическая.

3. у = хп,

п — нечетное натуральное число ^ 3:

D(f) = (-оо, +оо);

E(f) = (-оо, +оо);

нечетная: (—х)п = —хп

возрастает на (—оо, +оо);

неограниченная;

непериодическая.

1 х

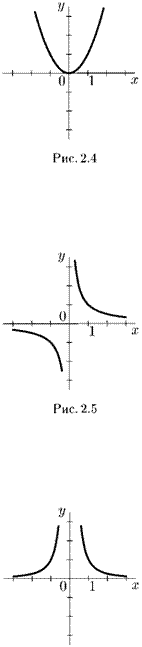4. у = хп,

п — четное натуральное число:

D(/) = (-oo, +оо);

E(f) = [О, +оо);

четная: (—х)п = хп

убывает на (—оо, 0), возрастает на [0, +оо);

неограниченная;

непериодическая.

5. у = х п,

п — нечетное натуральное число:

!>(/) = (-оо, 0)U(0, +с»);

E(f) = (-(X), 0)_U (0, +оо);

нечетная: (—х) п = —х п;

убывает на (—оо, 0) U (0, +оо);

неограниченная;

непериодическая.

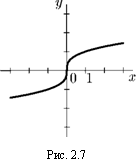
6. у = х~п, п — четное натуральное число:

D(/) = (-oo, 0)U(0, +оо);

£7(/) = (-оо, 0) U (0, +оо);

четная: (-х) п = х п]

возрастает на (—оо, 0), убывает на (0, +оо);

неограниченная;

непериодическая.

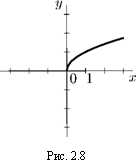
п — нечетное натуральное число:

£>(/) = (-оо, +оо);

E(f) = (-оо, +оо);

нечетная: Ц/—х = — \[х

возрастает на (—оо, +оо);

неограниченная;

непериодическая.

8. у= Цх,

п — четное натуральное число:

D(f) = [О, +оо);

E(f) = [0, +оо);

общего вида;

возрастает на [0, +оо);

неограниченная;

непериодическая.

2) показательные функции:

1. у = аж, 0 < а < 1:

£>(/) = (-оо, +оо); ^sL

E(f) = (0, +оо); і і і п^г

общего вида; 1

убывает на (—оо, +оо);

неограниченная;

непериодическая.

2 Я. М. Ахтямов

2. У = ах,

а > 1:

х

£>(/) = (-оо, +оо);

£/(/) = (0, +оо);

общего вида;

возрастает на (—оо, +оо);

неограниченная;

непериодическая.

Рис. 2.10

3) логарифмические функции:

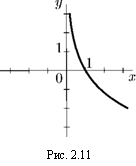
1. у = ogax, 0 < а < 1:

£>(/) = (0, +оо);

E(f) = (-оо, +оо);

общего вида;

убывает на (—ос, +оо);

неограниченная;

непериодическая.

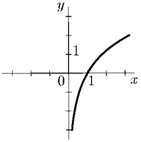
1. у = ogax, а > 1:

£>(/) = (0, +оо);

E(f) = (-оо, +оо);

общего вида;

возрастает на (—оо, +оо):

неограниченная;

непериодическая.

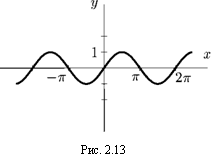4) тригонометрические функции: 1. у = sin х:

D(f) = (-оо, +оо);

E(f) = [-1, 1];

нечетная: sin(—х) = — sin ж;

возрастает на [-тг/2 + 2тгп, тг/2 + 2тггс], убывает на

[тг/2 + 2тгп, 37г/2 + 2тгп],

п Є Z;

ограниченная: | sin ж| ^ 1;

периодическая: sm(x + T) = sin ж, Т = 2тг.

2. у = cos ж:

£>(/) = (-оо, +оо);

ВД = [-1, 1];

четная: cos(—х) = cos ж;

убывает на

[27ГП, 7Г + 27ГП],

возрастает на

[—7Г + 27ГП, 7Г + 27ГП],

п Є Z;

ограниченная: |cosx| ^ 1;

периодическая:

cos(x + Т) = cos ж, Т = 2тг.

3. у = tgx:

1) W) =

= ( — 7г/2 + 7ГП, 7г/2 + 7Гп),

п Є Z;

2) = (-оо, +оо);

нечетная: tg (—ж) = — tgx;

возрастает на

( —7г/2 + 7ГП, 7г/2 + 7ГП),

п Є Z;

неограниченная;

периодическая:

tg(x + T)=tgx,T = 7r.

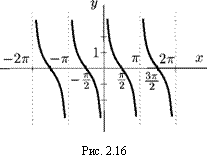3. у = ctgx:

D(f)= (тгп, тг + 7гп), п Є Z;

Я (/) = (-оо, +оо);

нечетная: ctg (—х) = —ctgx;

убывает на (7гп, тг + тгп),

п Є Z;

неограниченная;

периодическая:

ctg(x + T) = ctgx, Т = тг.

Я(/) = [-1, 1];

£(/) = [-7Г/2, +7Г/2];

нечетная: arcsin (—ж) = —arcsin ж;

возрастает на [—1, 1];

ограниченная: |arcsinx| ^ 7г/2;

непериодическая.

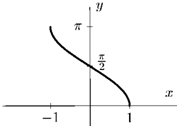
2. у = arccos х

£>(/) = [-1, 1];

E(f) = [О, тг];

общего вида:

arccos (—х) = 7г — arccos х;

убывает на [—1, 1];

ограниченная: 0 ^ arccos ж ^ 7г;

непериодическая.

D(f) = (-оо, +оо);

E(f) = (-7Г/2, тг/2);

нечетная: arctg (—х) = —arctgx;

возрастает на (—оо, +оо);

ограниченная: |arctgx| < 7г/2;

непериодическая.

4. у = arcctgx:

D(f) = (-оо, +оо);

E(f) = (О, тг);

общего вида:

arcctg (—х) = 7г — arcctgx;

убывает на (—оо, +оо);

ограниченная: 0 < arcctg ж < 7г;

непериодическая.