12.5. свойства определенного интеграла

12.5. свойства определенного интеграла

На протяжении всего параграфа будем предполагать интегрируемость рассматриваемых функций на выделенных отрезках интегрирования.

Рассмотрим сначала свойства определенного интеграла, которые имеют аналоги в случае интеграла неопределенного.

1. Постоянный множитель можно выносить за знак интеграла, т. е.

kf(x)dx = к

f(x)dx,

где к — некоторое число.

□ Отрезок [а, Ь] разобьем на отрезки [#г-ъ хі] и выберем точки сі на каждом из отрезков разбиения. Составим интегральную сумму

п г = 1

для функции к f(x). Используя распределительный закон умножения чисел, имеем

Y,kf(ci)Axi = к ^Ґ(сі)Ахі.

г=1 г=1

Переходя к пределу при тахДжї —> О в левой и правой частях последнего равенства и вынося множитель к в правой части из под знака предела, получаем

п п

t=l

lim Vfc f(ci) Ахі = к lim V/(c;)A^.

тахДж^->-0 .—; тахЛж^—>-0 .—

t=l

По определению определенного интеграла первый из пределов b b равен J к f(x) dx, второй равен к J f(x) dx. Ш

а а

2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т. е.

(f(x)±g(x))dx =

f(x)dx ±

g(x) dx.

□ Справедливо равенство

п п п

Z (f(ct) ± д(сг)) Ахі = Y,f(ci) Ахі ± Z)Axi-

t=l

t=l

t=l

Переходя в этом равенстве к пределу при max Ах і О, получаем

п

тахЛж^—>-0 .—: г=1

п п

тахЛж^—>-0 .—: тахЛж^—>-0 .—: г=1 г=1

Откуда

{f(x)±g(x))dx =

f(x)dx ±

g(x) dx.

Перейдем теперь к свойствам определенного интеграла, которые не имеют аналогов в случае неопределенного интеграла.

3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т. е. при любых а, 6, с:

f(x) dx =

f(x)dx +

f(x)dx.

При a < с < b это равенство имеет простой геометрический смысл (см. рис. 12.4, а). Согласно геометрическому смыслу определенного интеграла

ebb

f(x) dx = Si,

f(x) dx = S2,

f(x) dx = S,

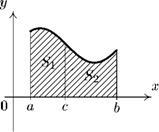
а б Рис. 12.4. Третье свойство определенного интеграла

где S — площадь всей заштрихованной фигуры. Тогда при сделанных предположениях третье свойство утверждает наличие следующего очевидного соотношения между площадями:

S = S1 + S2.

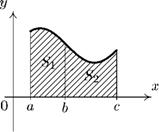
Другие случаи сводятся к данному. Например, если а < b < с, то согласно рис. 12.4, б):

b с с

f(x)dx = £i = S S2 =

f{x)dx

f{x)dx =

f(x)dx +

f(x) dx.

4. Если на отрезке [a, 6], где a < 6, f(x) < g(x), то и b b

f(x)dx ^

g(x) dx,

т. е. обе части неравенства можно почленно интегрировать.

□ Из неравенства f(x) ^ д(х) вытекает аналогичное неравенство для интегральных сумм:

п п

^2f(ci)Axi ^ ^д(сі) Ахі. t=l 1=1

Переходя к пределу при max Аж« —> 0, получаем

п п

тахДж^—>-0 .—: тахДж^—>-0 .—: г=1 г=1

f(x)dx ^

д(х) dx.

Следствие. Пусть на отрезке [а, 6], где а < 6, т ^ f(x) ^ М, где т и М — некоторые числа. Тогда

m(bа) ^ f(x) dx ^ М (Ь а).

□ По свойству 4 имеем ъ ъ mdx <

а а Ъ Ъ

f(x)dx^ Mdx.

а

Вычислим J т dx и J М dx. Для этого докажем сначала равенство

dx = b — а.

Подынтегральная функция равна единице: f(x) = 1; интегральная сумма для нее выразится формулой

п п

Y,f(Ci)^Xi = Y,^i =

t = l i = l

= (xi a) + (x2 xi) + (xs x2) + ... + (xn-i ~ xn-2) +

+ (b xn-i) = b a.

Далее, согласно свойству 1 имеем

mdx = т

dx = m(b — а),

а b

М dx = М

dx = М (bа),

откуда

m(b — а) ^

f(x) dx ^ M(b-a).

5. Теорема о среднем. Если функция у = f(x) непрерывна на отрезке [а, Ь] (где а < 6), то найдется значение с Є [а, 6], что

f(x)dx = f(c) (6-а).

□ По первой и второй теоремам Вейерштрасса непрерывная на отрезке [а, Ь] функция ограничена на нем и достигает своего наименьшего и наибольшего значения (см. раздел «Предел и непрерывность»), т. е.

т ^ f(x) ^ М, х Є [а, 6],

где m и М — наименьшее и наибольшее значения функции на [а, 6]. Тогда согласно только что доказанному следствию

m(b — а) ^

f(x)dx ^ М(6а),

или

т ^

/(ж) ^ М.

Но функция, непрерывная на отрезке, принимает любое значение, заключенное между наименьшим и наибольшим значениями (теорема Больцано-Коши). Поэтому, в частности, найдется такое число с Є [а, 6], что

f(x)dx = f(c).

Геометрический смысл теоремы о среднем. Пусть f(x) ^ 0 на [а, 6]. Найдется точка с из отрезка [а, 6], что площадь под кривой у = f(x) на [а, Ь] равна площади прямоугольника со сторонами f(c) и (b — а) (см. рис. 12.5, а).

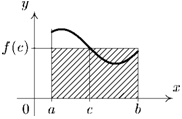12.6. Формула Ньютона-Лейбница

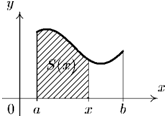
Рассмотрим функцию у = интегрируемую на отрезке [а, Ь]. Если х Є [а, 6], то функция /(£) интегрируема также на любом отрезке [а, 6]. Предположим, что х меняется на отрезке [а, 6], тогда на этом отрезке определена функция

Ф{х) =

/(*) Л-

Эта функция называется определенным интегралом с переменным верхним пределом.

Пусть/(ж) ^ 0 на отрезке [а, Ь]. Тогда значение функции Ф(х) в точке х равно площади S(x) под кривой у = f(x) на отрезке [а, х] (см. рис. 12.5, б). В этом состоит геометрический смысл интеграла с переменным верхним пределом.

Рассмотрим теперь свойства функции Ф(ж).

Теорема. Если подынтегральная функция f(x) непрерывна, то производная функции Ф(х) по переменному верхнему пределу существует и равна значению подынтегральной функции для этого предела, т. е.

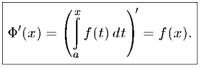Ф'(х) = hm Av у = /(ж). v ) Аж^о Дж J v )

Найдем АФ = Ф(х + Ах) Ф(х).

ж+Аж

ж+Аж

Дф = ф(ж + Дж) ф(ж) =

/(*) dt

f(t) dt =

f(t) dt.

По теореме о среднем найдется такое значение с Є [х, х + Дж], что

ж+Аж

/(*) rft = /(с) (ж + Ах х) = /(с) Да,

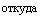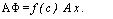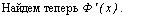Аж^О

Аж^О

Ф (ж) = 11 г г і v у = 11 г г і ^— = 11 г г і /(с).

Аж^О

Заметим, что с —» ж при Аж —>> 0, так как с Є [ж, ж + Дж]. Поэтому в силу непрерывности функции f(x) получаем:

Ф'(х)= \т f(c) = f(x). Ш

Аж—>-0

Следствие. Для любой непрерывной функции f(x) существует первообразная.

Действительно, в качестве такой первообразной всегда можно предъявить определенный интеграл с переменным верхним пределом Ф(ж), поскольку Ф'(х) = f(x).

Теорема (формула Ньютона—Лейбница). Пусть функция у = f(x) непрерывна на отрезке [а, Ь] и F(x) — произвольная первообразная для f(x) на [а, 6]. Тогда определенный интеграл от функции f(x) на [а, Ь] равен разности значений первообразной F(x) для верхнего и нижнего предела интегрирования, т. е.

f(x)dx = F(b) F(a).

□ Пусть F(x) — некоторая первообразная для функции f(x).

х

Функция Ф(ж) = ^f(t)dt также является первообразной для

а

функции f(x). Следовательно,

F(x)-<b(x) = C,

так как любые первообразные для одной и той же функции отличаются лишь на константу (см. с. 202). Отсюда

F(b) F(a) = (Ф(Ь) + С) (Ф(а) + С) = Ф(Ь) Ф(а) =

b a b b

f(x)dx

f(x)dx =

f(x)dx-0 =

f(x)dx.

Формула названа в честь Ньютона и Лейбница, хотя она была установлена еще Барроу, учителем Ньютона.

БАРРОУ (Barrow) Иссак (1630-1677) — английский математик, филолог, богослов. Родился в Лондоне. Крупным достижением Барроу является установление связей между операцией отыскания производной и операцией интегрирования. Он рассматривает интегрирование, по сути дела, как новую математическую операцию, с помощью которой можно решать многие задачи.

В 1669 г. он отказался от кафедры математики в Кембридже в пользу Ньютона, своего тезки и ученика.

Перед смертью Барроу произнес: «Наконец-то я узнаю решение многих геометрических и астрономических вопросов. О, господи, какой Ты геометр!»

Формула Ньютона-Лейбница сводит вычисление определенного интеграла к отысканию неопределенного интеграла. Чтобы

b

вычислить определенный интеграл |/(ж)с?ж, достаточно найти

а

неопределенный интеграл J f(x) dx, подставить в найденное выражение сначала верхний предел, затем нижний и вычесть вторую величину из первой.

Постоянное слагаемое неопределенного интеграла можно не выписывать: оно все равно уничтожится при вычитании.

2

V Пример 1. Найти J Зж2 dx.

-і

Решение. Находим неопределенный интеграл

3x2dx = x3 + C.

Подставив х = 2, находим 8 + С; при х = — 1 получаем — 1 + С. Вычитая вторую величину из первой, находим

2

J 3 х2 dx = (8 + С) (-1 + С) = 8 (-1) = 9. -і

Постоянное слагаемое С при вычитании уничтожилось. А

7Г

V Пример 2. Найти J sin х dx.

о

Решение. Имеем

sin х dx = — cos х + С.

Следовательно,

sin ж dx = — (cos7r — cosO) = 2. A

о

Разность F(b) — F(a) при вычислении интеграла часто записывают так:

ъ

F(x)

(читается: «F(x) с двойной подстановкой от а до 6») обозначает то же, что F(b) — F(a). Например, вместо — (cos7r — cosO) пишут — cos х

V Пример 3. Найти J

dx

Решение. Имеем

dx Л — = In х

x

= In еIn 1 = 1-0 = 1. А