21.7. выбытие фондов
21.7. выбытие фондов
Рассмотрим теперь еще одну математическую модель, описывающую рост количества продукции y(t) на некотором предприятии, произведенной в момент времени t. В отличие от модели естественного роста, когда к = const, и в отличие от модели Дж. Кьютелета (21.5), когда к = к(у), будем предполагать, что коэффициент к зависит от времени t: к = —k(t). (Знак «минус» означает, что фонды не увеличиваются, а выбывают.) Такое происходит, например, когда предприятие не вкладывает вырученные деньги в производство, и при этом с течением времени на предприятии происходит изнашивание оборудования и орудий труда, т. е. происходит выбытие фондов.
Тогда рост количества продукции y(t) на некотором предприятии, произведенной в момент времени t описывается не уравнением (21.6), а уравнением
y'(t) = -k(t)y(t),
У(0) = Уо
(21.9)
Рассмотрим два случая. Первый, когда k(t) = О, и второй, когда k(t) = 1.
г) См., например, Coleman J. S. Introduction to mathematical sociology. N. Y. Free Press of Glencoe, 1964.
 |
2. При постоянном выбытии фондов (например, при k(t) = 1) должно происходить падение производства. Решение соответствующего дифференциального уравнения дает именно это:
у = -<**; lnM = -t + ln|C|;
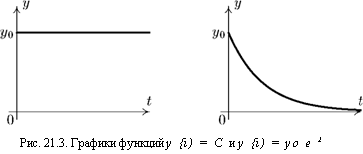
y(t) = уо е~г (убывающая функция).
Соответствующий график приведен на рис. 21.3.
В социальных науках и страховом деле уравнением (21.9) пользуются для определения вероятности того, что лицо доживет до возраста t. Решением уравнения (21.9) при учете начального условия у(0) = 1 будет функция
t
-$k(t)dz
y(t) = e 0
При составлении таблиц смертности для взрослого населения нередко пользуются формулой Макегама, согласно которой
k(t) = а + /3е7*, а > 0, /3>0, 7 > 0,
где значение коэффициентов се, /3, 7 определяется условиями, в которых находится группа лиц, подлежащих изучению, и, прежде всего, социальными условиями.
Формула Макегама выражает то, что взрослый человек может умереть от причин, не зависящих от возраста, и причин, зависящих от возраста. При этом вероятность смерти растет с увеличением возраста в геометрической прогрессии.
21.8. Рост производства с учетом инвестиций
Уравнение Дж. Кьютелета y(t) = к(у) y(t) исходит из замкнутости популяции и не учитывает миграции популяции, зависящей, вообще говоря, от у и t.
Если изучается население страны, то эта модель становится неприемлемой. Учет миграции приводит к уравнению
yf(t) = k(y)y(t) + u(t,y).
(21.10)
Здесь u(t, у) — величина, характеризующая миграцию. Она равна разности между количеством иммигрантов и эмигрантов. Если u(t,y) > 0, то это означает, что количество иммигрантов в момент времени t превышает количество эмигрантов.
В моделях экономического роста уравнение (21.10) характеризует рост выпуска продукции с учетом внешних инвестиций u(t, у) > 0.
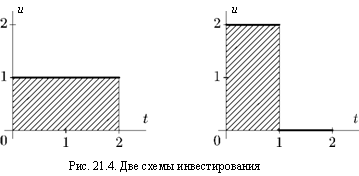
V Пример. Государство решает перечислить в течении двух лет в только созданное предприятие и расширение его производства денежную сумму 20 тыс. условных единиц. При этом оно должно выбрать одну из непрерывных схем финансирования, изображенных на рис. 21.4:
Первая схема. Перечислять каждый год по 10 тыс. у. е.
Вторая схема. Перечислить в первый год все 20 тыс. у. е., и во второй год не перечислять ничего.
 |
Какую из двух схем инвестирования должно выбрать государство, чтобы предприятие выпустило больший объем продукции?
Решение. Предприятие начинает с нуля и еще не в состоянии делать инвестиции. Поэтому считаем, что у(0) = 0. Государство вкладывает в каждый момент времени t сумму в u(t) денежных единиц. Поскольку в нашей упрощенной модели предполагается, что с момента создания первые же денежные инвестиции позволяют выпускать предприятию свою продукцию, то количество выпущенной продукции y(t) в денежном эквиваленте выражается уравнением
y'(t) = u(t), 2/(0) =0. (21.11)
Для первой схемы инвестирования имеем
u(t) = 1, при 0 < t < 2,
т. е.
y'(t) = 1, у(0) = 0,
откуда
y(t) = t, при 0 < t < 2.
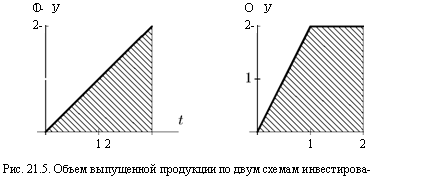
Объем Yi, выпущенной продукции за два года равен площади фигуры под графиком функции y(t). Площадь этой фигуры, представляющей собой треугольник (рис. 21.5), равна 2:
Yi = 0,5-2-2 = 2 (20 тыс. у. е.).
Для второй схемы инвестирования имеем:
u(t) = 2, при 0 < t < 1, u(t) = 0, при 1 < t < 2,
т. е.
!/'(*) = 2, у(0) = 0, при 0 < * < 1, y'(t) = 0 при 1 < t < 2,
откуда
| y(t) | = 2t, | при 0 < t < 1, |
| y(t) | = 2, | при 1 < t < 2. |
ния
Объем І2 продукции, выпущенной за два года по второй схеме инвестирования, равен площади трапеции (рис. 21.5). Стало быть, І2 = 3 (30 тыс. у. е.).
По второй схеме инвестирования предприятие выпустит продукции на общую сумму на 10 тыс. у. е. больше. Таким образом, вторая схема инвестирования выгоднее. А
Пример показывает, что предприятия в период становления нуждаются в поддержке государства больше, чем в более поздний период.
Задача 1. Государство решает перечислить в течении двух лет в только созданное предприятие и расширение его производства денежную сумму в 10 условных единиц. При этом оно должно выбрать одну из непрерывных схем финансирования:
u(t) = 51 или u(t) = 10 — 5 £.
Какую из двух схем инвестирования должно выбрать государство, чтобы предприятие выпустило больший объем продукции?
Ответ: вторую.
Объединим две последние модели — модель выбытия фондов и модель роста производства с учетом банковских инвестиций. Пусть предприятие производит нужную для государства продукцию. Как и в модели выбытия фондов, будем предполагать, что на предприятии происходит быстрое изнашивание оборудования и орудий труда и само предприятие не вкладывает вырученные деньги в производство (к = —k(t)). Денежные вложения в производство осуществляет лишь банк. Причем, в момент времени t поток капиталовложений составляет u(t) условных единиц и мгновенно преобразуется в расширение производства.
Тогда стоимость продукции y(t) на некотором предприятии, произведенной в момент времени £, описывается уравнением
y'(t) + k(t)y(t) = u(t). (21.12)
Дифференциальное уравнение (21.12) является обыкновенным линейным дифференциальным уравнением первого порядка. Знание его экономического смысла позволяет часто предугадывать свойства решения только по виду уравнения. Действительно, например, пусть задано линейное дифференциальное уравнение
У1 -У = ех,
или
У = У + ех.
Коэффициент при у является коэффициентом выбытия фондов. Он равен (—1). Следовательно, фонды не выбывают, а растут. Государственные капиталовложения в предприятие положительны (функция ех > 0). Здравый смысл подсказывает, что при таких условиях должен происходить рост производства. Поэтому, не решая самого дифференциального уравнения, мы можем сказать, что его решением является растущая функция. Так оно и есть на самом деле. После соответствующих математических выкладок получим, что решением этого дифференциального уравнения является
у[х) = С ех + хех
(растущая функция).
Аналогичный вывод мы можем сделать и для линейного дифференциального уравнения
/ х
У -~Г—^У = х-1 + х
Коэффициент выбытия фондов —2J отрицателен, значит
фонды прибывают. Инвестиции х растут. Следовательно, должен происходить рост производства. Решением уравнения должна быть растущая функция. После соответствующего решения действительно получим растущую функцию
у(х) = (Vl + х2 + С) л/l + х2
Слагаемое и в уравнении
y ) = -ky(t) + u,
выражавшее поток «внешних капиталовложений», может означать и другие внешние воздействия на предприятие. Слагаемое и может быть и отрицательным. В этом случае оно может выражать, например, какой-либо уход денег из предприятия (например, расходы или выплаты по налогам, издержки производства, потребительские расходы и т. п.). Поскольку издержки часто зависят не только от времени £, но и от объема выпуска продукции y(t) в момент времени £, то и является, вообще говоря, функцией от двух переменных t и у. Коэффициент к, как мы видели, также может зависеть и от переменной t и от переменной у. Таким образом, более общее уравнение роста может быть выражено более общим, вообще говоря, уже нелинейным, дифференциальным уравнением
y'(t) = k(t,y)y(t) + u(t,y). (21.13)
В частных случаях это уравнение может оказаться и уравнением с разделяющимися переменными, и линейным уравнением, и уравнением Бернулли. Знание его экономического смысла позволяет предугадывать свойства решения.
Если в микроэкономике наиболее употребимым линейным дифференциальным уравнением является уравнение (21.12), то в макроэкономике используется уравнение
(21.14)
Здесь t выражает время; y(t) — национальный доход; c(t) — потребление (более точно, непроизводственное потребление, прирост материальных оборотных средств, государственных матери і dy(t)
альных резервов, потери); к ——— — накопление основных производственных фондов.
Уравнение (21.14) характеризует тот факт, что национальный
. dy(t) ,
доход разделен на две части: накопление к ^ (первое слагаемое в правой части уравнения) и потребление c(t) (второе слагаемое в правой части уравнения), причем накопление производится государством пропорционально приросту национального дохода
в тот же момент времени. Коэффициент к выражает капиталоемкость национального дохода (отношение производственного накопления к приросту национального дохода).
Модель, основанная на уравнении (21.14), является простейшей моделью экономической динамики. С помощью нее находят динамику национального дохода у (і) в зависимости от траектории потребления c(t).
Задача 2. Не интегрируя дифференциальное уравнение у'-^ = х, х>1, 2/(1) = 1, зная лишь экономический смысл коэффициентов (коэффициент
з
выбытия фондов равен , инвестиции равны ж), определить
X
возрастает или убывает функция, задающая решение. Ответ: возрастает.
Задача 3. Проинтегрировать уравнение из предыдущей задачи.
Ответ: у = 2 х3 — х2.
Задача 4. Решить задачу Коши
2/'-^ = 1, х>1, 2/(1) = 1Придать этой задаче несколько социальных и экономических интерпретаций, пояснить полученное решение.
Задача 5. Придать уравнению Бернулли
yf + l = -Xy2
экономический смысл. Проинтегрировать его и объяснить экономический смысл решения.
Ответ: у = 9 . Решение — убывающая функция, так
х + Сх
как происходит выбытие фондов и капитала.
Обсуждение Математика для социологов и экономистов
Комментарии, рецензии и отзывы
