12.8. геометрические приложения определенного интеграла
12.8. геометрические приложения определенного интеграла
Формула Ньютона-Лейбница
f{x)dx = F(b) F(a)
представляет универсальную формулу вычисления площадей. С помощью этой формулы можно находить площади квадратов, прямоугольников, треугольников, трапеций и других более сложных фигур.
Действительно, площадь квадрата со сторонами, равными 2, равна
2
2
2 dx = 2 х
о

 |
площадь прямоугольника со сторонами 1 и 2 равна
і
2 dx = 2 х
о
= 2,
о
площадь прямоугольного треугольника с катетами 2 и 2 равна
2
х dx =
= 2,
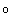 о
о
площадь трапеции с основаниями 1, 2 и высотой 1 равна
2
ж = —
(рис. 12.6).
Теорема. Пусть на отрезке [а, Ь] заданы непрерывные функции у = /і(ж) и у = f2(x) такие, что f2(x) ^ fi{x). Тогда площадь фигуры, заключенной между кривыми у = f2(x) и у = fi(x), на отрезке [а, Ь] вычисляется по формуле (рис. 12.7, а)
S =
{f2(x)-h(x))dx.
□ Будем предполагать, что у = fi(x) и у = f2(x) — неотрицательные функции на [а, Ь]. Этого всегда можно добиться путем параллельного переноса оси Ох.
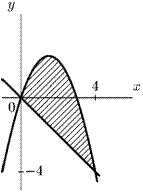
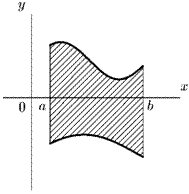 а б Рис. 12.7. Вычисление площадей
а б Рис. 12.7. Вычисление площадей
Искомую площадь можно рассматривать как разность двух криволинейных трапеций, ограниченных данными линиями. Поэтому
S = #2 — Si =
f2(x) dx
fi(x) dx =
(f2{x) dx fi{x)) dx.
Заметим, что разность f2(x) — f(x) представляет «толщину» фигуры в точке ж, а площадь S представляет собой «сумму» по х от а до b всех «кусочков» с переменной «толщиной» f2(x) fi(x). Ш
V Пример 1. Вычислить площадь фигуры, ограниченной линиями у = 3 х — х2 и у = —х.
Решение. Найдем точки пересечения данных кривых. Для этого решаем систему уравнений
(у = 3хх^ у = -х.
Решив ее, получаем:
х = О, х2 = 4, у = 0, у2 = -4.
Строим искомую фигуру (см. рис. 12.7, б). График параболы расположен выше прямой. Поэтому f2(x) = Зж — ж2, а /і(ж) = —ж.

S =
fi{x)) dx = ((3х х2) (-х)) dx = о
4
(4x-x2)dx= (2x2-^pj
0
= Ю-. A
V Пример 2. Найти площадь фигуры, ограниченной линиями у = у/х и у = х2.
Решение. Вычислим координаты точек пересечения указанных кривых, для чего решим систему уравнений:
(у = х2, у = VхРешив ее, получаем:
Xl = 0, х2 = 1, У = 0. г/2 = 1.
Строим искомую фигуру. Она похожа на лепесточек (рис. 12.8). График параболы у = х2 расположен ниже кривой у = у/х (в этом можно убедиться сравнив ординаты в какой-либо промежуточной между нулем и единицей точке, например, в точке X = = 1/2). Поэтому /2(х) = \[х , a fi(x) = х2. Следовательно,
S = (/2(3?) — fi(x)) dx = (л/^~ — ^ж —
а О
2 3/2 _^
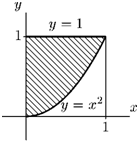
V Пример 3. Найти площадь фигуры, ограниченной параболой у = х и прямыми = 0 и ;/у = 1.
Решение. Фигура, ограниченная указанными линиями, изображена на рис. 12.8 под названием «уголочек». Площадь этой фигуры вычисляется по формуле
S =
(1
і dx =
х
= 1-1= 2-.
з з
Площадь «лепесточка» внутри квадрата оказалась в три раза меньше площади самого квадрата, а площадь «уголочка» — в два раза больше площади «лепесточка». А
Задача 1. Вычислить площадь фигуры, ограниченной параболой
1
у = ^(х + 6)2
и прямой
2х-у + 12 = 0.
Ответ: 12 кв. ед.
Объем тела вращения. Пусть на отрезке [а, Ь] задана непрерывная неотрицательная функция у = f(x). Необходимо найти объем Vx тела, образованного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями у = /(ж), у = 0. х — а. х — b (рис. 12.1).
Ученые XVIII века находили объем тела вращения следующим образом. Они считали, что криволинейная трапеция состоит из бесконечно малых прямоугольников со сторонами dx и f(x) (рис. 12.2). При вращении каждого такого прямоугольника вокруг оси абсцисс получается диск, имеющий толщину dx и радиус R = f(x) (рис. 12.9). Объем диска Vd равен объему цилиндра с радиусом R = f(x) и высотой Н = dx:
Vd = 7rR2H = 7rf2(x)dx.
«Просуммировав» объемы всех таких дисков, ученые получали следующую формулу:
vd =
Vd =
7Г f2(x) dx.
Эта формула действительно справедлива. Рассуждения ученых были качественно верными. Однако термин бесконечно малая величина не был ими достаточно четко определен, что приводило к противоречиям. Поэтому по форме такие рассуждения в современной математике считаются неприемлемыми х) и заменяются доказательствами, основанными на теории предела.
Докажем полученную формулу, пользуясь понятиями предела и интегральной суммы. Разобьем отрезок [а, Ь] на более мелкие отрезки точками:
а = хо < х < Х2 < ... < хп = b
и на каждом из отрезков разбиения выберем точку где і = = 1, 2, ..., п (рис. 12.10). При вращении вокруг оси Ох каждый прямоугольник с высотой f(ci) и основанием Ахі = х{ — х{описывает цилиндр с радиусом f(ci) и высотой Ах і. Сумма объемов всех цилиндров
п
5>/2(с;)Д^
г=1
приближенно равна объему Vx тела вращения (рис. 12.10). Очевидно, что приближение для искомого объема Vx будет тем лучше, чем меньше длина отрезков разбиения Аж^, поэтому за искомый объем Vx естественно взять следующий предел:
п
тахЛж^—>-0 .—: г=1
х) Исключение составляет так называемый нестандартный (или неархиме-дов) анализ, зародившийся в 60-х гг. XX в., где вводится четкое определение бесконечно малой величины как некоего гипердействительного числа.
 |
a dx
№
/(*)
н >
вращаемый прямоугольник диск толщиной dx
Рис. 12.9. Vd = 7г f2(x)dx
У
У
 №
№
а Axj
х
—>
х
 |
вращаемая фигура
тело вращения
Рис. 12.10. Vx = lim Р(сі)Ахі
тахДжі^О ^ = 1
где тахАжі —> 0 — максимальная из длин отрезков разбиения. Но выражение
п
5>/2(С;)Д*г
г=1
есть не что иное, как предел интегральной суммы для функции д(х) = 7г/2(ж), поэтому по определению определенного интеграла получаем
| Ь | |
| Vx = ir | fx)dx. |
| С | і |
Заменим формально в этой формуле переменную ж на і/. Получим формулу
| d | |
| Vy = ir | 92{у) dy. |
| С | |
Она выражает объем тела, полученного от вращения криволинейной трапеции вокруг оси Оу.
 V Пример 4. Найти объем тела, полученного вращением вокруг оси Ох области, ограниченной параболой у = х2 и прямыми у = 0, х = 1 (рис. 12.11).
V Пример 4. Найти объем тела, полученного вращением вокруг оси Ох области, ограниченной параболой у = х2 и прямыми у = 0, х = 1 (рис. 12.11).
V
вращаемая фигура тело вращения
і
Рис. 12.11. Vx = 7г ^(x2)2dx о
Решение. Имеем а = О, b = 1, f(x) = х2, откуда
У, = 7Г
f2(x) dx = 7Г
(х2)2 dx = 7Г ^— 5
1 1
= -7Г. А
о 5
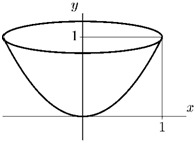
V Пример 5. Найти объем тела, полученного вращением вокруг оси Оу области, ограниченной параболой у = х2 и прямыми у = і, ж = 0 (рис. 12.11).
 | |||
 | |||
і
Рис. 12.12. Ц, = тг J(V^)2 dy
Решение. Имеем с = О, d = 1, = д/у , откуда d і
Vy = 7T
g2(y)dy = 7г
ydy = >K —
1 1
= -7Г. А
о 2
Задача 2. Вычислить объем тела, полученного вращением вокруг оси Ох криволинейной трапеции, ограниченной линиями у = -, х = 1, у = 2. Ответ: 30 7г.
Задача 3. Вычислить объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной линиями у2 = 4 — х2, х = 0. ^12
Ответ: — тг « 107,23.
15
Обсуждение Математика для социологов и экономистов
Комментарии, рецензии и отзывы
