10.4. принцип акселерации

10.4. принцип акселерации

Рассмотрим некоторое предприятие, выпускающее потребительскую продукцию у. Зададимся вопросом: как инвестиции в расширение производства этого предприятия влияют на рост его продукции? Очевидно, увеличение инвестиций i(t) ведет к росту продукции y(t). Но весь вопрос состоит в том в каких размерах это происходит. Как эту зависимость выразить аналитически?

Предположим, что с некоторого начального момента времени t = 0 инвестиции отсутствуют; тогда выпуск продукции должен остаться на прежнем уровне, т. е. если i(t) = 0, то y(t) = у(0) (рис. 10.2).

2/(0)

0

о

Рис. 10.2. Выпуск продукции в условиях отсутствия инвестиций

о

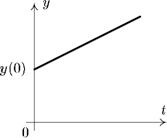
Рис. 10.3. Выпуск продукции в условиях постоянного инвестирования

Если же предприятие инвестируется, причем инвестиции постоянны, то производство постоянно расширяется и выпуск продукции должен линейно расти, т. е. y(t) = ct + у(0) при i(t) = = b > 0 (рис. 10.3).

Выразить из этих графиков зависимость между переменными i(t) и y(t) с помощью алгебраических уравнений невозможно.

Наилучшим уравнением, выражающим эти графические зависимости между i(t) и y(t), является не алгебраическое уравнение, а уравнение, содержащее вместо переменной ее производную:

dt

dy(t)

= ki(t). (10.8)

Уравнение (10.8) достаточно точно отражает реальную ситуацию. Действительно, если i(t) = 0 из (10.8) получаем — 0

или y(t) = const = у(0); если же i(t) = 6, то = kb или

y(t) = kbt + y(0).

Вывод: рост инвестиций ведет не столько к росту продукции, сколько к скорости роста, причем скорость роста прямо пропорциональна увеличению инвестиций.

* * *

В реальной рыночной экономике предприятие не может бесконечно увеличивать рост своей продукции. Оно увеличивает производство только в том случае, если есть спрос на его продукцию. Предприятие должно мгновенно реагировать на изменения спроса q(t) и выпускать продукции ровно на столько больше на сколько больше увеличивается спрос, т. е. предприятие должно выпускать продукцию y(t) так, чтобы она совпадала по величине со спросом q(t) на нее:

V(t) = q(t).

Из этого уравнения и равенства (10.8) получаем, что для того, чтобы удовлетворить этим требованиям, инвестиции должны удовлетворять уравнению

dq(t) dt

= ki(t).

После введения нового обозначения а = —, получаем

к

i[t) = а

dqjt) dt

(10.9)

Вывод: Для полного удовлетворения спроса и полной реализации своей продукции предприятие должно увеличивать инвестиции пропорционально скорости роста спроса (акселерации).

Коэффициент пропорциональности а = называют коэффик

циентом акселерации или акселератором.

* * *

Пусть спрос на продукцию предприятия растет. Должны ли инвестиции также возрасти? Многие скажут: конечно, должны. И будут неправы. Ответ на этот вопрос не является однозначным, как иногда думают. Все зависит от того, каков знак второй производной от функции спроса — плюс или минус.

Если знак функции q" (t) — плюс, то q'(t) строго возрастает. Из (10.9) следует, что тогда должны возрастать и инвестиции i(t).

Если знак q"(t) — минус, то q'(t) строго убывает, а это означает, что инвестиции i(t) также должны убывать.

Если вторая производная q"(t) равна нулю на некотором промежутке, то q'(t) постоянна на этом промежутке. Следовательно, должны быть постоянными и капиталовложения в производство.

Вывод:

1. Если спрос на предметы потребления возрастает в

каком-либо периоде все быстрее (qff(t) > 0), то должны

возрастать и капиталовложения в их производство.

Если спрос на предметы потребления с какого-то момента начинает расти все медленнее (qff(t) < 0), то должны уменьшиться и размеры капиталовложений.

Если спрос на предметы потребления возрастает с постоянным темпом, достигнутым в момент времени to5 то капиталовложения следует удерживать на уровне достигнутом в момент времени to (рис. 10.3).

Приведенное положение называют принципом акселератора.